Модуль 1. Принцип динамического расширения—сжатия фазового пространства в теории управления

1.5. Принцип динамического расширения—сжатия фазового пространства

В соответствии с теорией АКАР законы управления (1.2) обеспечивают обязательный перевод ИТ системы (1.1) из произвольного начального состояния в окрестность заданного многообразия $\psi=0$ (1.3) или пересечения многообразий $\psi_s=0$ (1.11). Размерность подпространства этих многообразий, куда попадет ИТ в результате действия указанных законов управления, равна $n-1$ — для скалярного или $n-m$ — для векторного управлений соответственно. Выше была установлена тесная связь многообразий (1.3) и (1.11) с инвариантными соотношениями в механике, технике и вообще в естествознании.

Возникает важный вопрос о направлении и свойствах дальнейшего движения ИТ вдоль указанных многообразий под действием синтезируемых управлений. Другими словами, необходимо разработать общий принцип такого деформирования фазового пространства динамической системы под действием внутренних управлений, при котором ИТ могла бы пройти “вглубь” подпространства многообразий (1.3) или (1.11) с последующим попаданием в начало координат или на заданное финишное многообразие согласно основной задаче управления.

В предыдущих разделах уже обсуждалась постановка основной задачи синтеза замкнутой системы, которая в общем виде обычно ставится как определение такого закона управления в функции координат состояния, который переводит изображающую точку (ИТ) объекта $n$-го порядка из произвольного начального состояния $x_{10},i=1,\dots,n$ в заданное конечное состояние, например в начало координат фазового пространства.

Подчеркнем тот очевидный факт, на который почему-то редко обращают внимание, что в начальный момент $t=0$ ИТ находится в пространстве размерности $n$, в конечный же момент, т.е. после завершения процесса управления, ИТ попадает в точку $\mathbf x_k(0,\dots,0)$ с нулевой размерностью. Это означает, что под действием управления ИТ постепенно переходит из исходного пространства размерности $n$ в подпространство размерности $n-1$, затем $n-2$, $n-3$ и т.д. вплоть до одномерного многообразия $\dim(\psi_s)=1$, двигаясь вдоль которого на финишном участке ИТ и попадает в начало координат фазового пространства. Другими словами, под действием непрерывного управления происходит постепенное сжатие объема фазового потока, в котором движется ИТ объекта.

1.5.1. Фазовый поток в диссипативных системах

Строгое определение понятия фазового потока приведено в [38, 39]. Пусть для динамической системы $M$ — фазовое пространство детерминированного процесса, тогда точка этого пространства представляет определенное состояние процесса. Если в момент $t=0$ процесс был в состоянии $\mathbf x$, то в другой момент состояние процесса будет уже $\mathbf G^t\mathbf x$ (где $\mathbf G^t$ — однопараметрическая группа преобразований за время $t$), т.е. для каждого $t$ определено отображение $\mathbf G^t:M\to M$ фазового пространства процесса в себя. Именно однопараметрическая группа преобразований множества $M$ и называется фазовым потоком с фазовым пространством $M$. В физическом плане можно, например, представить себе фазовое пространство заполненным жидкостью, тогда частица $\mathbf x$ через время $t$ переходит в точку $\mathbf G^t\mathbf x$, а орбиты фазового потока являются фазовыми траекториями. Под действием фазового потока ИТ движется так, что вектор скорости системы в каждый момент времени равен вектору фазовой скорости в той точке фазового пространства, где находится ИТ системы. Поэтому фазовым потоком векторного дифференциального уравнения
$$
\dot {\mathbf x}(t)=\mathbf {F(x)}
$$ называется однопараметрическая группа диффеоморфизмов (гладких преобразований), для которой $\mathbf F$ является векторным полем фазовой скорости. Для того, чтобы найти фазовый поток дифференциального уравнения, достаточно решить это уравнение [38, 39]. Напомнив эти фундаментальные понятия современной теории дифференциальных уравнений, вернемся к явлению сжатия фазового объема в системах управления.

Предположим теперь, что синтезирован закон разрывного, например кусочно-непрерывного, управления объектом. В этом случае очевидно, что указанное сжатие фазового объема будет происходить скачком в определенные моменты времени. В качестве примера, подтверждающего это положение, рассмотрим задачу синтеза законов оптимального по быстродействию управления. Дело в том, что теория оптимального по критерию быстродействия управления в концептуальном плане является вершиной в современной теории автоматического управления по сравнению с любыми другими критериями качества. С одной стороны, оптимальное по быстродействию управление непосредственно отражает динамическую парадигму естествознания, основанную на пространственно-временном подходе, а с другой стороны, известно, что к задаче быстродействия может быть сведена задача оптимизации системы по любому другому критерию, отличному от критерия быстродействия. Указанная процедура сведения осуществляется путем расширения фазового пространства исходной системы на одну дополнительную координату, равную соответствующему критерию качества. Предположим, что объект является неосциллирующим и описывается дифференциальными уравнениями
$$
\dot x_1(t)=x_2, \quad \dot x_2(t)=u, \quad |u|\le u_{\max}.\qquad
(1.18)$$Известно [40], что закон оптимального по быстродействию управления объектом (1.18) имеет следующий вид:
$$
u(x_1,x_2)=-u_{\max}\mathrm{sign}\,\mu(x_1,x_2)=-u_{\max}\mathrm{sign}\left(x_1 + \frac{0,5}{u_{\max}}x_2|x_2|\right).\qquad
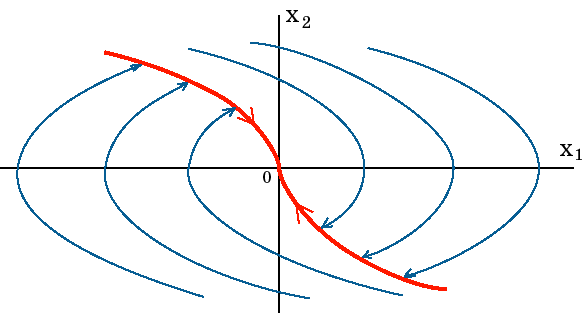
(1.19)$$Закон (1.19) обеспечивает двухинтервальное управление $\pm u$ по переводу ИТ из произвольного начального состояния $(x_{10},x_{20})$ в начало координат (0,0) фазовой плоскости (рис. 1.1). При этом на первом интервале ИТ движется по полутраектории, имеющей размерность $\dim x=2$, однако в момент переключения $t=t_1$ знака управления происходит сжатие площади фазового потока. Далее ИТ будет двигаться теоретически по линии переключения $\mu(x_1,x_2)=0$, имеющей размерность, равную уже $\dim \mu=1$. Покажем, что это действительно так. Уравнение линии переключения согласно (1.19) имеет вид

$$
\mu(x_1,x_2)=x_1+ \frac{0,5}{u_{\max}}x_2|x_2|=0.\qquad
(1.20)$$ Тогда с учетом первого уравнения объекта (1.18) из (1.20) получим
$$
\dot x_1(t)|\dot x_1(t)| + 2u_{\max}x_1(t)=0\qquad
(1.21)$$ или
$$
\dot x_2(t) + u_{\max}\mathrm{sign} x_2(t)=0.\qquad
(1.22)$$Дифференциальные уравнения (1.21) или (1.22}, описывающие движение ИТ вдоль линии переключения (1.20) относительно $x_1(t)$ или $x_2(t)$ соответственно, имеют уже размерность $\dim \mu=1$, хотя исходный объект имел $\dim \mathbf x=2$. Итак, на линии переключения (1.20) произошло сжатие фазового объема, а ИТ, двигаясь вдоль этой линии, в момент $t=t_2$ прибывает в начало координат $\dim \mathbf O=0$ фазовой плоскости замкнутой системы (1.18), (1.19). Подчеркнем, что сжатие площади фазового потока происходит скачком в момент переключения управления и попадания ИТ на линию переключения.

Рис. 1.1. Фазовый портрет оптимальной по быстродействию системы 2-го порядка

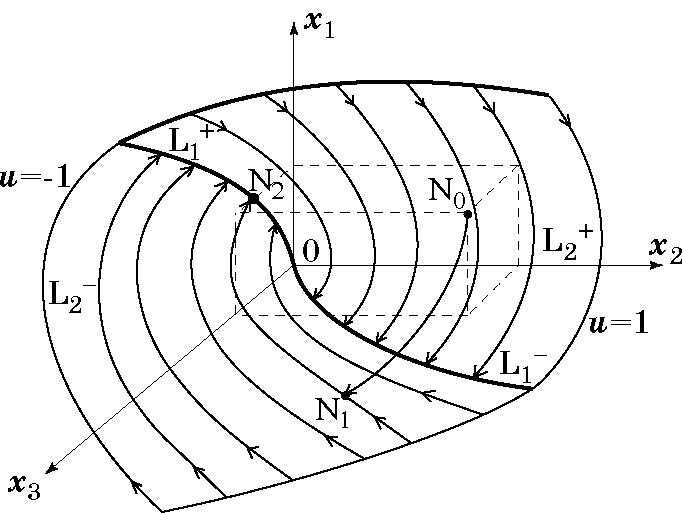
Рис. 1.2. Фазовый портрет оптимальной по быстродействию системы 3-го порядка

Аналогичная картина движения ИТ имеет место и при оптимальном по быстродействию трехинтервальном управлении $\pm u_{\max}$ неосциллирующими объектами третьего порядка (рис. 1.2). В этом случае ИТ движется на первом интервале по полутраектории $\mathbf{N}_0 \mathbf {N}_1$, стартуя, например, из точки $\mathbf N_0$, находящейся в трехмерном пространстве $\dim \mathbf x=3$. В момент первого переключения $t=t_1$ управления ИТ попадает в точке $\mathbf N_1$ на двумерную $\dim \mathrm L_2=2$ поверхность переключения $ \mathrm L_2$, при этом происходит первое сжатие объема фазового потока. Далее, двигаясь вдоль $ \mathrm L_2$, ИТ в момент второго переключения $t=t_2$ попадает в точке $\mathrm N_1$ на одномерную $\dim \mathrm L_1=1$ линию $\mathrm L_1$, являющуюся “краем” поверхности переключения $\mathrm L_2$, при этом происходит второе сжатие фазового объема. Затем, двигаясь по линии $\mathrm L_1$, ИТ в момент $t=t_3$ обязательно попадает в начало координат, имеющее нулевую размерность.

Итак, в рассмотренном оптимальном по быстродействию процессе (рис. 1.2) происходит скачкообразное $\pm u_{\max}$ трехкратное сжатие фазового объема, в результате чего ИТ, начиная свое движение из точки, находящейся в исходном трехмерном пространстве, попадает в начало координат фазового пространства с нулевой размерностью. В связи с тем, что в течение оптимального процесса знаки управляющего воздействия $\pm u_{\max}$ чередуются на соседних интервалах, то концы множества фазовых полутраекторий предпоследнего интервала $ \mathrm L_2^-$ (рис. 1.2) будут принадлежать полутраектории $\mathrm L_1^+$ и, следовательно, концы полутраектории $ \mathrm L_2^+$ будут принадлежать полутраектории $\mathrm L_1^-$. В своей совокупности полутраектории второго интервала $ \mathrm L_2^+$ и $ \mathrm L_2^-$ образуют две двумерные поверхности, которые стыкуются по одномерной линии $\mathrm L_1$. Эти поверхности, имеющие в качестве края линию $\mathrm L_1$, образуют в целом поверхность переключения $\mathrm L_2$, двигаясь вдоль которой ИТ попадает на линию $\mathrm L_1$ и далее в начало координат. Это означает, что, попав в момент $t=t_1$ на двумерную поверхность $\mathrm L_2$, ИТ будет находиться на ней в течение двух последних интервалов вплоть до окончания в момент $t=t_3$ оптимального по быстродействию процесса [28, 40].

Аналогичным образом происходит процесс сжатия фазового объема при оптимальном по быстродействию управлении объектами более высокого $(n>3)$ порядка. В этом случае, продолжая предыдущие рассуждения, нетрудно показать, что полутраектории $\mathrm L_3^+$ и $\mathrm L_3^-$, концы которых соответственно располагаются на поверхностях $\mathrm L_2^+$ и $\mathrm L_2^-$, образуют в своей совокупности трехмерное многообразие $\mathrm L_3$. Далее, продолжая указанное построение, последовательно получим многообразия $\mathrm L_4,\mathrm L_5,\dots,\mathrm L_{n-1},\mathrm L_n$. Отсюда непосредственно следует, что каждое многообразие $\mathrm L_k$, в свою очередь, принадлежит многообразию $\mathrm L_{k+1}$ и разбивает его на две области $\mathrm L_{k+1}^+$ и $\mathrm L_{k+1}^-$, а все полутраектории из семейства $\mathrm L_{k+1}^+$ заканчиваются на $\mathrm L_{k+1}^-$ и, следовательно, все полутраектории $\mathrm L_{k+1}^-$ заканчиваются на многообразии $\mathrm L_{k}$. Очевидно, что для неосциллирующих объектов задача синтеза в конечном итоге сводится к поиску непроницаемого многообразия $\mathrm L_{n-1}$, разбивающего фазовое пространство $\mathrm L_{n}$ на две области, в одной из которых $u(t)=+u_{\max}$, а в другой $u(t)=-u_{\max}$. При этом многообразие $\mathrm L_{n-1}$ включает в себя многообразия $\mathrm L_{n-2},\mathrm L_{n-3},\dots,\mathrm L_2$, и, наконец, одномерную линию $\mathrm L_1$, двигаясь по которой ИТ попадает на многообразие $\mathrm L_0$, состоящее из единственной точки (начала координат) и имеющее нулевую размерность.

Итак, начав движение в исходном фазовом пространстве $\mathrm L_n$, ИТ в результате первого переключения знака управления сначала попадает на многообразие $\mathrm L_{n-1}(\dim \mathrm L_{n-1}=n-1)$, например $\mathrm L_{n-1}^-$, двигаясь по которому она попадет на многообразие $\mathrm L_{n-2}^+$, затем на $\mathrm L_{n-3}$, $\mathrm L_{n-4}$ и т.д. В конечном итоге ИТ попадает на двумерную поверхность $\mathrm L_2$ и после последнего переключения знака управления $t=t_{n-1}$ она по одномерной линии $\mathrm L_1$ приходит в начало координат фазового пространства.

Подчеркнем, что при оптимальном по быстродействию процессе ИТ последовательно переходит от одного многообразия $k$-ой размерности $(\dim \mathrm L_k=k)$ к следующему многообразию $(k-1)$-ой размерности $(\dim \mathrm L_{k-1}=k-1)$, при этом сжатие фазового объема происходит в точках переключения знака управляющего воздействия.

Разумеется, что описанная выше картина движения ИТ в фазовом пространстве является в определенной мере математической идеализацией, т.к. в реальных условиях переключение управления с одного знака $(+u_{\max})$ на другой $(-u_{\max})$ происходит не мгновенно, а за определенное время, кроме того, могут существовать неучтенные малые запаздывания и т.д. В результате при реальном оптимальном по быстродействию управлении ИТ будет двигаться не абсолютно точно по соответствующей гиперповерхности переключения $\mathrm L_k$, а в некоторой ее окрестности, т.е. в некотором “пограничном слое”, находящемся в сжимающемся фазовом потоке. Однако описанная выше картина движения ИТ при идеальном оптимальном по быстродействию процессе позволяет четко и наглядно выявить такое фундаментальное свойство, как эффект сжатия объема фазового потока при переходе ИТ с одного многообразия на другое подмногообразие пониженной размерности вплоть до попадания в начало координат фазового пространства замкнутой системы. В этом эффекте как раз и состоит, помимо прочих достоинств, одна из замечательных, концептуальных особенностей оптимальных по быстродействию систем. Очевидно, что выявленный эффект сжатия фазавого объема имеет весьма важное общетеоретическое значение для проблемы синтеза систем управления.

Рассмотренный процесс сжатия фазового объема в оптимальных по быстродействию системах, когда ИТ попадает и затем движется по многообразиям последовательно понижающейся размерности $\mathrm L_{n-1},\mathrm L_{n-2},\dots,\mathrm L_1,\mathrm L_0$, может быть интерпретирован как процесс попадания и движения ИТ вдоль желаемого оптимального многообразия, обладающего свойством минимальности времени движения. В этом случае желаемое многообразие $\psi=0$ не задается каким-либо произвольным образом, а находится в результате строгой процедуры синтеза гиперповерхности переключения. Аналогичное положение имеет место и при оптимизации систем не по быстродействию, а по другим критериям качества. Это означает, что в оптимальных системах применение метода АКАР связано с выявлением оптимальных многообразий, входящих в соответствующие законы управления. При этом определяющее значение для поиска многообразий имеет заданный критерий оптимальности синтезируемой системы.

Описанные выше и представленные на рис. 1.1 и рис. 1.2 процессы сжатия фазового потока происходили в оптимальных по быстродействию системах, являющихся исходно нелинейными. Но оказывается, что сходные явления наблюдаются и в линейных системах, свойства которых, как известно, существенно зависят от корней характеристического уравнения $\lambda_1$. В этой связи рассмотрим линейную систему в трехмерном фазовом пространстве и воспользуемся замечательными графическими иллюстрациями из работы [38]. В этом случае характеристическое уравнение представляет собой вещественное кубическое уравнение, которое может иметь три вещественных корня или один вещественный и два комплексных. Решение линейного дифференциального уравнения третьего порядка, как известно, имеет следующий вид:
$$
x(t)=C_1\exp(\lambda_1 t) \xi_1 +C_2\exp(\lambda_2 t) \xi_2 + C_1\exp(\lambda_3 t) \xi_3,\qquad
(1.23)$$где $\xi$ — какой-нибудь собственный вектор с собственными значениями $\lambda_k$, $k=1,2,3$. Выберем эти значения вещественными, тогда с учетом того, что $\exp(\lambda t)$, $(\mathrm{Re} \lambda<0)$ при $t\to\infty$ стремится к нулю тем быстрее, чем меньше $\mathrm{Re} \lambda$, получим, согласно выражению
$$
x(t)=\mathrm{Re}\left(C_1\exp(\lambda_1 t) \xi_1 +C_2\exp(\lambda_2 t) \xi_2 + C_1\exp(\lambda_3 t) \xi_3\right),
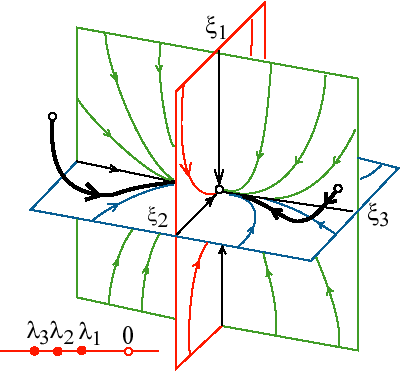
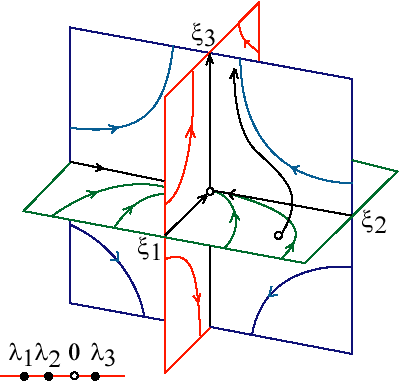
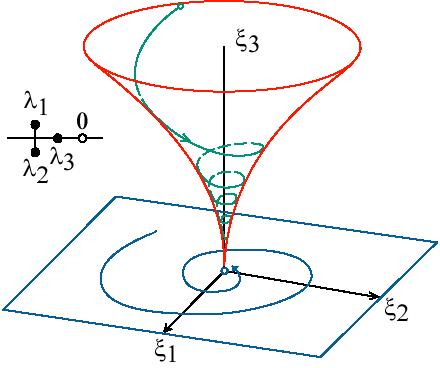
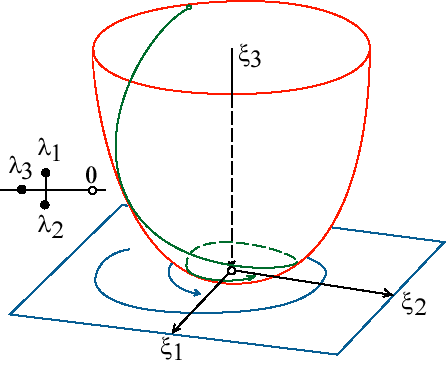
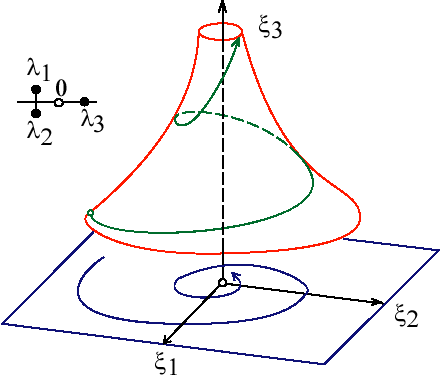
$$соответствующие фазовые траектории. На рис. 1.3, рис. 1.4, рис. 1.5, рис. 1.6, рис. 1.7 изображены фазовые потоки, которые имеют следующие отличия: на рис. 1.3 изображено фазовое пространство в случае $\lambda_3<\lambda_2<\lambda_1<0$, при этом фазовый объем сжимается по трем направлениям, т.е. по общему направлению к нулевой точке; на рис. 1.4 представлен случай $\lambda_1<\lambda_2<0<\lambda_3$, при этом фазовый поток сжимается по двум направлениям $\xi_1$, $\xi_2$ и растягивается по третьему $\xi_3$; на рис. 1.5 показан случай $\mathrm{Re} \lambda_{1,2}<\lambda_3<0$, при этом фазовый объем сжимается по направлению $\xi_3$, а в плоскости ($\xi_1$, $\xi_2$) наблюдается вращение с более быстрым сжатием: на рис. 1.6 изображен случай $\lambda_3<\mathrm{Re} \lambda_{1,2}<0$, при этом фазовый объем сжимается по направлению $\xi_3$, а в плоскости ($\xi_1$, $\xi_2$) наблюдается вращение с более медленным сжатием; и, наконец, на рис. 1.7 показан случай $\mathrm{Re} \lambda_{1,2}<0<\lambda_3$, при этом фазовый объем растягивается по направлению $\xi_3$, а в плоскости ($\xi_1$, $\xi_2$) наблюдается вращение со сжатием фазового объема [38, 39].

Рис. 1.3. Фазовое пространство системы при $\lambda_3<\lambda_2<\lambda_1<0$

Рис. 1.4. Фазовое пространство системы при $\lambda_1<\lambda_2<0<\lambda_3$

Рис. 1.5. Фазовое пространство системы при $\mathrm{Re}\lambda_{1,2}<\lambda_3<0$

Рис. 1.6. Фазовое пространство системы при $\lambda_3<\mathrm{Re}\lambda_{1,2}<0$

Рис. 1.7. Фазовое пространство системы при $\mathrm{Re}\lambda_{1,2}<0<\lambda_3$

Изображенные на рис. 1.3, рис. 1.4, рис. 1.5, рис. 1.6, рис. 1.7 процессы движения ИТ в трехмерном фазовом пространстве весьма наглядно показывают характер поведения фазовых траекторий в линейных устойчивых (рис. 1.3, рис. 1.5 и рис. 1.6 и неустойчивых (рис. 1.4, рис. 1.7) динамических системах третьего порядка. В нелинейных же системах третьего порядка их фазовое пространство может быть как аналогичным рис. 1.3, рис. 1.4, рис. 1.5, рис. 1.6, рис. 1.7, так и иметь принципиально иное поведение фазовых траекторий. Более того, в фазовом пространстве нелинейных динамических систем третьего порядка возможно появление некоторых множеств “странных аттракторов” с парадоксальными свойствами, которые принципиально невозможны в линейных системах.

Наличие фундаментального свойства сжатия фазовых площадей и объемов у рассмотренных выше динамических систем указывает на принадлежность к классу диссипативных систем [41]. Это свойство противоположно свойству сохранения площадей и объемов в фазовом пространстве у консервативных (гамильтоновых) систем, которое, как известно, следует из свойства сохранения энергии у такого рода систем. В консервативных системах исходный элемент фазового потока переносится вдоль траектории без деформации либо экспоненциально удлиняется со временем (как $\exp(\lambda\cdot t)$, $\lambda>0$) в одном направлении и одновременно сжимается (как $\exp(-\lambda\cdot t)$, $\lambda>0$) в перпендикулярном ему направлении. Но так как $\exp(\lambda\cdot t)\cdot \exp(-\lambda\cdot t)\equiv1$, то площадь или объем во втором случае также сохраняются [41]. В динамическом отношении в первом случае траектории движения устойчивы, а во втором — неустойчивы.

Для консервативных систем характерна инвариантность их свойств относительно обращения времени, что свидетельствует о сохранении их энергии. В диссипативных же системах обращение времени приводит к кардинальному изменению их свойств, в частности, к эффекту сжатия их фазового объема, что указывает на рассеивание энергии. Диссипативные системы могут обладать весьма многообразными режимами, в особенности когда их динамика включает в себя как эффекты затухания, так и механизмы, поддерживающие их движение, при этом объем этих систем в фазовом пространстве всегда не сохраняется, а динамика необратима. Другими словами, диссипативным системам обязательно присуще свойство сжатия площадей или объемов в фазовом потоке. Однако это вовсе не означает, что в этих системах невозможно расхождение, т.е. неустойчивость траекторий движения. В действительности в них могут возникать режимы, когда сокращение площадей или объемов достигается не только за счет сокращения всех длин, а в результате существенного сокращения одних длин при менее быстром сокращении других.

Иначе говоря, при общем сокращении площадей или объемов в фазовом пространстве диссипативных систем по некоторым направлениям их траектории могут разбегаться и движение по этим направлениям будет неустойчивым. Свойство разбегания траекторий объясняется необратимостью процессов, при этом сжимающийся и растягивающийся слои фазового потока будут соответствовать двум реализациям динамики, каждая из которых отражает эффект нарушения временной симметрии и парное появление несимметричных режимов. В этом случае сжимающийся слой в фазовом пространстве отвечает состоянию системы в будущем, а растягивающийся — в прошлом, т.е. налицо две реализации с противоположной ориентацией по времени [42].

Ранее уже отмечалось, что второе начало термодинамики, как принцип отбора, допускает только те начальные условия, в которых система эволюционирует к будущему равновесному состоянию. Эти качественные особенности диссипативных систем обязательно следует учитывать при разработке методов синтеза замкнутых нелинейных систем.

1.5.2. Аттракторы и сжатие фазового объема

Нелинейные диссипативные динамические системы обладают свойством притяжения траекторий, проходящих через определенную область фазового пространства, к некоторому многообразию, называемому аттрактором. По определению [41], аттрактором $\mathrm A$ называется некоторое компактное множество в фазовом пространстве, имеющее следующие основные свойства:

во-первых, аттрактор $\mathrm A$ инвариантен относительно действия фазового потока, т.е. $\mathrm{A\Phi\equiv A}$;

во-вторых, аттрактор имеет нулевой объем в $n$-мерном фазовом пространстве динамической системы;

в-третьих, аттрактор находится в некоторой области ненулевого объема, которая является областью притяжения данного аттрактора, т.е. в фазовом пространстве системы существует некоторое множество таких точек, что выходящие из них траектории при $t\to\infty$ всегда устремляются к аттрактору.

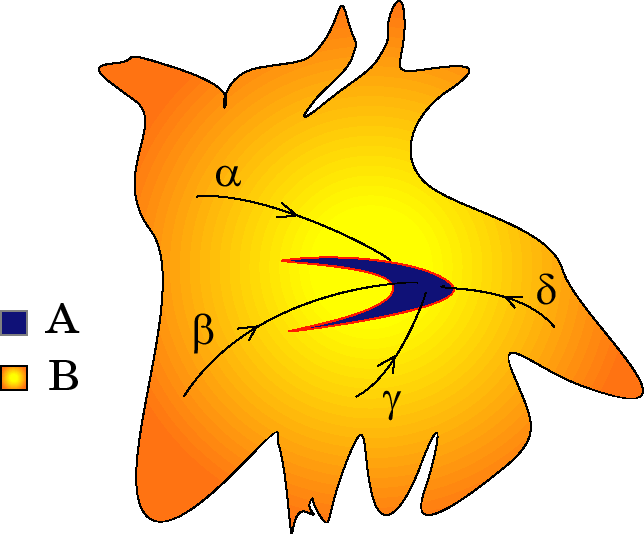
На рис. 1.8, взятом из [41], схематически изображен аттрактор $\mathrm A$ и его область притяжения $\mathrm B$. Траектории, выходящие из точек $\alpha$, $\beta$, $\gamma$ и $\delta$, переносятся фазовым потоком $\Phi$ к аттрактору. В математическом плане аттрактор представляет собой асимптотический предел решений дифференциальных уравнений нелинейной диссипативной системы, причем начальные условия этих решений должны обязательно лежать в области притяжения.

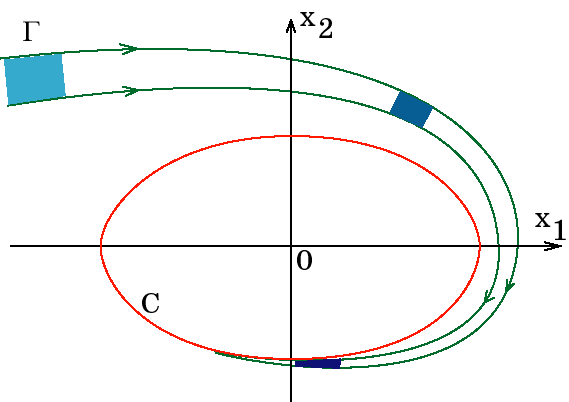
Для того, чтобы нагляднее показать особенности, возникающие при сжатии фазового объема, рассмотрим, следуя [41], фазовый портрет нелинейной диссипативной системы второго порядка с аттрактором в виде предельного цикла. Для этого предположим, что множество начальных условий на фазовой плоскости, откуда стартует ИТ, занимает некоторую область $\Gamma$ (рис. 1.9). В результате диссипации фазовый поток приводит к сокращению площади $\Gamma$ по мере движения ИТ до некоторого линейного отрезка на аттракторе $\mathrm C$ — предельном цикле, имеющем размерность $\dim \mathrm C$. Это означает, что происходит потеря информации относительно взаимного расположения исходных начальных условий в области $\Gamma$ фазовой плоскости. После достижения ИТ аттрактора $\mathrm C$ информация об исходных начальных условиях полностью утрачивается, что является следствием эффекта сжатия площади фазового потока и наличия аттрактора системы. Учитывая, что никаких особенностей у рассматриваемой системы, кроме наличия аттрактора, не предполагалось, то этот факт означает справедливость указанного свойства для любого другого типа аттрактора, а именно: свойства потери информации о начальных условиях старта ИТ системы.

Рис. 1.8. Аттрактор и его область притяжения

Рис. 2.9. Иллюстрация сокращения площадей в фазовом пространстве

Аналогичные свойства будут присущи и нелинейным системам третьего порядка, имеющим аттрактор в виде некоторого двумерного тора в трехмерном фазовом пространстве. Изображенные на рис. 1.8 и рис. 1.9 аттракторы лежат на некоторых многообразиях и сами образуют многообразия в фазовом пространстве системы. В частности, предельный цикл является простым многообразием, что предполагает наличие касательной в каждой его точке. Изложенные свойства аттракторов позволяют сделать общий важный вывод: размерность $(m)$ аттрактора всегда меньше размерности $(n)$ фазового пространства исходной динамической системы, т.е. $m<n$. В соответствии с [41] приведем некоторые количественные соотношения, являющиеся следствием описанного выше свойства сокращения объемов (площадей) в фазовом пространстве нелинейных диссипативных систем. Для этого определим относительную скорость изменения гиперобъема $V$ в фазовом пространстве под действием фазового потока, найдя следующую производную Ли:
$$
\frac 1 V \frac {dV}{dt}=\sum\limits_{i=1}^n\frac{\partial \dot x_j}{\partial x_i}<0,\qquad
(1.24)$$где $x_i$ — $i$-я координата фазового пространства вектора замкнутой системы.

Известно, что для диссипативных систем величина (1.24) всегда отрицательна и может служить некоторой мерой сжатия фазового потока. Из (1.24) непосредственно следует, что в случае отрицательности производной $$\sum\limits_{i=1}^n\dfrac{\partial \dot x_j}{\partial x_i}<0$$ при $t\to\infty$ после попадания ИТ на аттрактор любое множество начальных условий объемом (площадью) отображается в множество нулевого объема [41]. Это становится очевидным, если представить выражение (1.24) в виде
$$
\frac 1 V \frac {dV}{dt}=-b, \quad b>0.
$$

Отсюда непосредственно следует, что при $t\to\infty$ объем $V\to 0$, т.е. объем (площадь) самого аттрактора всегда равен нулю. Это важный и нетривиальный вывод, следующий из свойства сжатия фазового потока в диссипативных системах.

Таким образом, к важнейшим для метода АКАР свойствам диссипативных нелинейных систем относятся, во-первых, “потеря” ими памяти о начальных условиях, откуда начинает свое движение ИТ системы, и, во-вторых, обязательное снижение размерности аттрактора по сравнению с размерностью фазового пространства исходной системы.

В последнее время исследование динамики нелинейных диссипативных систем привело к открытию так называемых “странных аттракторов” с весьма своеобразными свойствами. Дело в том, что в обычных динамических системах вследствие детерминистского подхода к их изучению фазовые траектории принципиально не должны пересекаться в фазовом пространстве. В противном случае одно начальное условие могло бы породить разные фазовые траектории, т.е. система после точки пересечения траекторий могла вести себя совершенно по-разному, а ее поведение оказалось бы совершенно непредсказуемым. Именно эта базовая установка лежит в основе известной детерминистской доктрины, согласно которой в детерминированных динамических системах невозможно хаотическое поведение. Однако в действительности оказалось, что в фазовом пространстве нелинейных детерминированных систем, имеющих размерность три и выше, при определенных видах нелинейностей и сочетании параметров принципиально могут существовать аттракторы, обладающие весьма необычными свойствами, а именно: близкие траектории, попавшие на такой аттрактор, начинают быстро расходиться. В результате на аттракторе возникает хаотический режим движения, отличительным свойством которого является чрезвычайная чувствительность к заданию начальных условий, находящихся на аттракторе. Внешне же фазовые траектории, имеющие начальные условия вне аттрактора, стремятся к аттрактору и “оседают” на нем. Но самой удивительной особенностью этих аттракторов является их нецелая размерность (например, $2<m<3$), которая получила название фрактальной размерности. Аттракторы, обладающие указанными весьма необычными свойствами притягивающего хаоса, получили в литературе [43, 41, 44] название “странных аттракторов”.

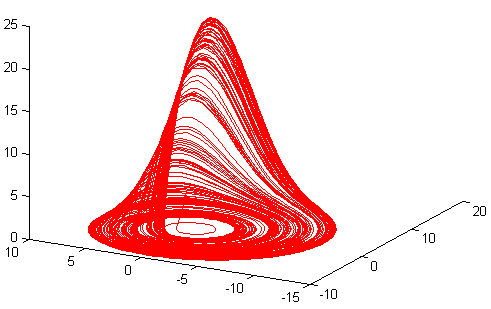
К “странным аттракторам” относится известный аттрактор Лоренца. На рис. 1.10 приведен пример другого распространенного “странного аттрактора” Ресслера для достаточно простой по структуре нелинейной динамической системы третьего порядка
$$
\begin{split}
\dot x(t)&=-y-z,\\
\dot y(t)&=x+ay,\\
\dot z(t)&=bx - cz + xz,
\end{split}\qquad
(1.25)$$имеющей лишь одну нелинейность $xz$. В окрестности начала координат фазового пространства система (1.25) имеет следующие особенности [45]: фазовые траектории отталкиваются от нулевой точки вдоль некоторой двумерной поверхности, а сама нулевая точка схожа с неустойчивым фокусом, и далее траектории притягиваются вдоль некоторой линии. Из рис. 1.10 следует, что конфигурация фазового пространства динамической системы со “странным аттрактором” Ресслера обладает парадоксальными свойствами: с одной стороны, она приводит к неустойчивости движения, что служит основным источником хаотического движения; а с другой стороны, одновременно не исключается возврат неустойчивых траекторий в окрестность начала координат фазового пространства, что, вообще говоря, ведет к формированию устойчивого аттрактора. Такого рода “странные аттракторы” подробно изучаются в обширной современной научной литературе [43, 41, 44] и др. Открытие этих аттракторов в динамике нелинейных систем явилось крупнейшей научной сенсацией нашего времени, способной привести к кардинальному изменению существующего взгляда на динамическую парадигму современного естествознания. Действительно, представляется неординарной и удивительной возможность возникновения хаотических режимов движения в детерминированной нелинейной системе третьего и более высокого порядков без какого-либо внешнего воздействия на эту систему.

Рис. 1.10. Аттратор Ресслера

Очевидно, что наличие “странных аттракторов” в синтезируемой системе может оказаться нежелательным, т.к. тогда система, построенная, например, в соответствии с положениями классической линейной теории управления, в режимах больших отклонений может оказаться вовсе неработоспособной из-за влияния нелинейностей и дрейфа или “старения” ее параметров, приводящих к эффекту “странного аттрактора”. В этом случае система приобретает свойства своего рода “черной дыры” в ее фазовом пространстве. Это будет означать, что при попадании ИТ системы в область притяжения “черной дыры” она неизбежно устремится к указанной “дыре” и будет находиться там сколь угодно долго. И так как “черная дыра” не совпадает с желаемым технологическим режимом работы объекта, то такая ситуация приведет к разрушению объекта, взрывам и т.п. По-видимому, участившиеся в последнее время катастрофы в сложных современных технических системах являются результатом не только ошибок эксплуатационного персонала, но и, может быть, следствием той ущербной линейной идеологии классической теории управления, которая была положена конструкторами этих систем в основу их проектирования. Учет нелинейных явлений в динамических объектах становится обязательным при создании эффективных сложных систем.

При проектировании многих систем необходимо синтезировать законы управления объектами таким образом, чтобы “странные аттракторы” либо не могли возникнуть при любых сочетаниях параметров объекта и системы управления, либо они обладали желаемыми динамическими свойствами. В настоящее время в литературе, к сожалению, практически отсутствуют пригодные критерии выявления “странных аттракторов” в фазовом пространстве динамических систем, тем более для определения свойств и параметров указанных аттракторов. Достаточно надежной гарантией отсутствия “странных аттракторов” в фазовом пространстве синтезируемой системы является ее свойство асимптотической устойчивости по Ляпунову в определенной области или в целом. Для обеспечения этого важного свойства необходимо осуществить структурное деформирование фазового пространства замкнутой системы путем конструирования соответствующих законов управления. Это означает, что синтезируемые законы управления должны содержать такие нелинейные функции координат, которые позволили бы осуществить желаемую деформацию фазового пространства системы.

Итак, изложенные выше важные и новые положения из динамики нелинейных систем показывают, что при управлении различными объектами происходит процесс сжатия фазового объема вплоть до попадания ИТ на конечное, желаемое многообразие — аттрактор соответствующей размерности. В качестве таких финишных многообразий в обычных задачах управления нередко выступает точка, например начало координат фазового пространства, имеющая нулевую размерность ($\dim \mathbf O=0$), или предельный цикл с $\dim \mathbf C=1$. В общем же случае в зависимости от технологической задачи управления указанные финишные многообразия могут иметь разнообразные формы. Так, например, в известной задаче управления космическим аппаратом осуществляется его перевод на желаемое многообразие — круговую или эллиптическую орбиту в центральном поле сил с заданной скоростью вращения аппарата относительно центра. Для других подвижных или технологических объектов эти конечные многообразия имеют другую форму. Разумеется, что желаемые конечные многообразия не должны противоречить естественной, природной сущности и динамическим свойствам исходного объекта.

Рассмотренные выше положения касались процесса сжатия фазового объема в динамических системах. Аналогично можно пойти и в обратном направлении, т.е. путем расширения фазового пространства. Эта процедура необходима, в частности, при синтезе систем управления, инвариантных относительно неизмеряемых возмущений заданного класса. В этом случае к исходной системе дифференциальных уравнений объекта добавляется некоторая дополнительная подсистема $\mathbf z$ уравнений $\mu$-го порядка, решением которой и является возмущение как функция времени. Между введенной подсистемой и исходными уравнениями должна быть установлена некоторая связь в виде соответствующего уравнения. Таким образом, производится расширение фазового пространства исходного объекта на $\mu$ координат, т.е. новая, расширенная система будет иметь общую размерность $\dim(\mathbf x +\mathbf z)=n + \mu$. Осуществив далее процесс сжатия фазового объема в этой расширенной динамической системе до желаемого финишного многообразия, можно тем самым синтезировать соответствующий закон управления. В результате этого будет построен так называемый динамический регулятор, обеспечивающий селективную инвариантность замкнутой системы к определенному классу возмущающих воздействий.

Итак, процесс управления — это по существу всегда процесс сжатия (или сначала расширения с последующим сжатием) фазового объема, в котором движется ИТ замкнутой системы. Синтез же законов управления, реализующих указанный процесс сжатия фазового объема, должен включать в себя регулярную процедуру перевода ИТ с одного заранее вводимого многообразия $k$-й размерности на следующее многообразие $(k-1)$-й размерности вплоть до финишного, желаемого многообразия.

1.5.3. 0сновные положения синергетического подхода в теории управления

В общем плане можно утверждать, что синтезируемая система управления должна обладать достаточным числом степеней свободы для реализации поставленной технологической задачи управления. Это означает, что в тех случаях, когда исходный объект обладает ограниченным числом степеней свободы $n$, то для реализации поставленной цели управления, заключающейся, например, в отслеживании или подавлении некоторой функции, представляемой решением дифференциального уравнения размерности $\dim \mathbf z=r$, необходимо предварительно осуществить операцию расширения фазового пространства исходного объекта, по меньшей мере до размерности $\dim(\mathbf x +\mathbf z)=n + r$. Отсюда следует важный вывод о том, что для синтеза эффективных систем управления следует предварительно произвести тем или иным способом добавление стольких степеней свободы, сколько было бы достаточным для реализации цели управления. Это положение корреспондируется с известным в кибернетике законом Эшби [46] о необходимом разнообразии. Здесь только понятие “разнообразие” конкретизируется в понятии “степени свободы” системы, т.к. именно степени свободы служат источником возможного разнообразия. Изложенные выше соображения позволяют сделать следующие общие важные выводы о задачах управления при синтезе систем:

• во-первых, управление объектом произвольной природы представляет собой организованный и целенаправленный процесс редукции избыточных степеней свободы исходной системы, т.е. все избыточные по отношению к заданной цели (финишному многообразию) степени свободы редуцируются и в конечном итоге остаются только те степени свободы, которые определяют цель управления;
• во-вторых, применительно к развиваемому в этой книге синергетическому подходу процедура редукции степеней свободы означает формирование между координатами системы некоторых связей — инвариантных многообразий (синергий), которые и реализуют указанную редукцию степеней свободы системы. При этом инвариантные многообразия (“редукторы степеней свободы”) вводятся в синтезируемую систему с помощью соответствующего закона управления;
• в-третьих, редуцируемые степени свободы замкнутой системы представляют собой элементы управления как некоторые системные категории, а инвариантные многообразия (синергии) ограничивают разнообразие системы и формируют связи, т.е. некоторые акции управления [47].

Таким образом, управление — это преодоление избыточных степеней свободы системы, а сами понятия “инвариантное многообразие” (синергия) и “избыточность” степеней свободы являются базовыми элементами синергетической теории управления. Именно избыточность и инварианты приводят к организованному поведению замкнутой системы. Подчеркнем важное свойство этой постановки проблемы управления — сначала следует создать избыточные степени свободы, которые определяют дополнительные возможности в свойствах будущей системы, а затем преодолеть (редуцировать) эти степени свободы в процессе управления. В синергетике указанный процесс отражает свойство самоорганизации нелинейных диссипативных систем. Именно описанные здесь новые понятия положены в основу развиваемого в данной книге синергетического подхода к синтезу систем управления нелинейными объектами различной природы.

Перейдем теперь к определенной конкретизации и применению изложенного выше принципа динамического расширения-сжатия фазового потока. Итак, управление — это редукция степеней свободы исходной сформированной (расширенной) системы дифференциальных уравнений. Отсюда следует, что исходная расширенная система в потенции обладает определенными априорными возможностями, которые больше и структурно выше в смысле перспектив возникновения новых свойств по сравнению со свойствами той или иной результирующей (замкнутой) системы, получаемой в итоге соответствующих процедур синтеза. Дело в том, что результирующая система — это исходная система с наложенными связями, отражаемыми в структуре синтезируемого закона управления. Уменьшение числа степеней свободы происходит за счет сил взаимодействия наложенных связей в направлении от начального положения ИТ к промежуточным состояниям на некоторых многообразиях понижающейся размерности ($\psi_1=0,\dots,\psi_m=0$) и далее к конечному многообразию. В результате такого взаимодействия в синтезированной системе генерируется энергия, необходимая для движения ИТ от исходного до конечного, желаемого многообразий. При этом в процессе движения ИТ от одного инвариантного многообразия к другому меньшей размерности расходуется соответствующее количество энергии, которое постепенно снижается и к моменту попадания ИТ на конечное многообразие становится минимальным или нулевым в зависимости от вида конечного многообразия системы. Движение вдоль каждого многообразия $\psi_{ks}=0$ реализуется за счет внутренних управлений системы, т.е. в процессе самодвижения к соответствующему аттрактору — инвариантному многообразию в фазовом пространстве. Свойства и направление этого процесса зависят не столько от внешнего принудительного управления, а в большей мере от внутренней динамики нелинейного объекта. Эта автономность движения будет проявляться тем больше, чем ближе находится объект к сильно неравновесной области своего состояния. С точки зрения синергетики движение синтезируемых систем на финишных многообразиях может быть интерпретировано как движение на желаемых диссипативных структурах, представляющих coбoй некоторые динамические состояния систем и отражающих их взаимодействие с окружающей средой [42].

1.5.4. Декомпозиция задачи синтеза и первые интегралы

В процессе описанного перехода ИТ от одного многообразия к другому происходит своего рода “игнорирование” части переменных системы. Число этих переменных равно числу многообразий $\psi_k=0$, последовательно (или параллельно) вводимых в процессе синтеза замкнутой системы управления. Эти особенности как раз и отражают процесс сжатия фазового объема в системах, синтезируемых на основе синергетического подхода. В математическом плане указанный процесс сжатия реализуется путем последовательного вложения друг в друга первых интегралов дифференциальных уравнений замкнутой системы. Так, при скалярном управлении $(m=1)$ осуществляется следующий последовательный переход от многообразия к многообразию:
$$
\begin{split}
&\psi_1(x_1,\dots,x_n)=0\to \psi_2(\psi_1,x_1,\dots,x_{n-1})=0\to\dots\\
&\to \psi_s(\psi_1,\dots,\psi_{s-1},x_1,\dots,x_{n-s})=0, \quad s\le n-1.
\end{split}
$$В случае же векторного управления ($m>1$) сначала осуществляется параллельное введение совокупности $m$ первых интегралов, т.е.
$$
\psi_1(x_1,\dots,x_n)=0,\dots,\psi_m(x_1,\dots,x_n)=0.
$$Затем на пересечении этих многообразий осуществляется аналогично скалярному управлению последовательное вложение $r$ первых интегралов друг в друга, т.е.
$$
\begin{split}
&\psi_{m+1}(x_1,\dots,x_{n-m})=0 \to \psi_{m+2}(\psi_{m+1},x_1,\dots,x_{n-m-1})=0 \to \dots\\
&\to\psi_r(\psi_{m+1},\dots,\psi_{n-m-r},x_1,\dots,x_{n-m-r})=0, \quad r\le n-m-1.
\end{split}
$$Другими словами, при последовательном $(m=1)$ введении $s$ первых интегралов образуется один общий первый интеграл $\psi_s=0$, а при параллельно-последовательном ($m>1$) введении образуется $m$ первых интегралов будущей замкнутой динамической системы. Для реализации изложенного процесса сжатия фазового объема необходимо соответствующим образом синтезировать законы управления. Именно эти управления вводят в замкнутую систему соответствующую энергию, в результате чего происходит изменение состояния системы, которое проявляется в изменении градиентов $\left(\dfrac{d\psi_s(x_1,\dots,x_n)}{dt}\neq0\right)$ в ее фазовом пространстве и, как следствие, изменяется скорость движения ИТ системы. Иначе говоря, синтезируемые управления служат причиной динамического взаимодействия соответствующих компонентов (тел, полей и др.) системы, что и приводит к деформации ее фазового пространства. Указанные управления представляют собой некоторые физические процессы, которые взаимодействуют с объектом и определяют его “внешние степени свободы”. Однако многие нелинейные объекты обладают “внутренними степенями свободы”, т.е. их динамика может во многом определяться внутренними взаимодействиями.

В любой системе управления можно выделить внешние и внутренние связи, налагаемые на координаты ее состояния. Внешние связи определяются видом и числом $(m)$ независимых каналов управления. Это позволяет сразу же осуществить динамическую декомпозицию системы до многообразия $(n-m)$-й размерности, которое является гиперповерхностью пересечений введенных $(m)$ инвариантных многообразий. Внутренние же связи определяются структурой исходной системы дифференциальных уравнений $(n-m)$-й размерности, которая отражает физические (химические, биологические, экономические и т.д.) закономерности, определяющие назначение объекта и замкнутой (“объект-регулятор”) системы. Дальнейшая декомпозиция образованных ранее $(n-m)$ уравнений — это установление соответствующих внутренних связей (синергий), т.е. навязывание желаемых соотношений $\psi_s(x_1,\dots,x_n)=0$ между координатами синтезируемой системы. Для описания движения декомпозированной системы на вводимых многообразиях $\psi_s(x_1,\dots,x_n)=0$ могут использоваться различные комбинации переменных состояния, удобные для отражения естественных свойств объектов в процедуре синтеза систем управления.

Предложенный общий подход к синтезу законов управления, основанный на идее сжатия фазового объема путем введения совокупности задаваемых первых интегралов, в определенной мере подобен методу Н.Г. Четаева [48, 49] в теории устойчивости. Согласно этому методу функции Ляпунова формируются в виде связки заранее найденных первых интегралов возмущенного движения. Известно, что это один из редких и весьма эффективных способов построения функций Ляпунова в теории асимптотической устойчивости. Отсюда, между прочим, следует, что в излагаемом подходе существенно упрощается проблема устойчивости, которая в конечном итоге сводится к исследованию устойчивости движения вдоль финишного многообразия, описываемого дифференциальными уравнениями $(n-\lambda m)$ размерности, где $\lambda$ — число вводимых многообразий. Указанная аналогия связывает принцип сжатия фазового объема с методом первых интегралов в теории устойчивости движения.

Необходимо особо подчеркнуть, что в отличие от обычного метода синергетики [43, 41, 44] и стандартного метода малого параметра нелинейной механики [18, 12], в которых параметры порядка находятся путем приближенной разнотемповой декомпозиции исходной системы (разбиения на медленные и быстрые подсистемы), предложенный здесь принцип сжатия фазового объема позволяет однозначно сформировать желаемые инвариантные многообразия $\psi_s(x_1,\dots,x_n)=0$, т.е. управляемые параметры порядка, в результате асимптотически точной динамической декомпозиции. Такая декомпозиция осуществляется путем сжатия фазового объема под действием синтезируемых внешних и внутренних управлений. Именно описанный выше эффект сжатия фазового объема и следующая из него точная динамическая декомпозиция являются теми базисными положениями, на которых построен синергетический подход к синтезу многомерных и многосвязных систем управления нелинейными объектами различной природы.

Таким образом, в основе развиваемого синергетического подхода лежат два фундаментальных принципа естествознания — это, во-первых, принцип инвариантности (сохранения) и, во-вторых, принцип расширения-сжатия фазового объема динамических систем. Принцип инвариантности, как известно, является базовым для всех наук, однако его использование в развиваемом синергетическом подходе имеет кардинальное отличие: если в естественно-научном подходе инварианты (синергии) отыскиваются “апостериори”, то в предлагаемом здесь подходе инварианты задаются “априори” с целью наделения синтезируемой динамической системы желаемыми синергетическими свойствами.