Задачи для самостоятельного решения
Для объектов, описанных в задачах 1–15, синтезировать методом АКАР закон управления, обеспечивающий выполнение поставленной цели управления. Проанализировать устойчивость замкнутой системы.
Для объектов, заданных в задачах 16–21, на основе принципиальной схемы составить математическую модель. Для полученных объектов синтезировать методом АКАР закон управления , обеспечивающий выполнение поставленной цели управления – стабилизации напряжения. Проанализировать устойчивость замкнутой системы.
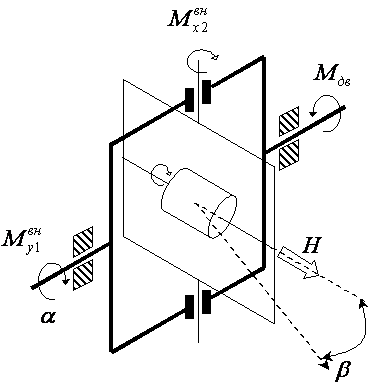
Задача 1. Одноосный силовой гироскопический стабилизатор на неподвижном основании
|
Математическая модель
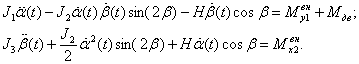
– угол поворота
наружной рамки относительно основания;
– угол отклонения оси ротора гироскопа от нормали к
плоскости наружной рамки (угол прецессии);
– кинетический момент
гироскопа;
– моменты инерции гиростабилизатора,
и
– моменты внешних сил,
приложенные к осям рамок,
– момент
стабилизирующего двигателя.
Переменные состояния:
,
,
,
.
Управляющие воздействия:
Параметры модели:
;
;
;
.
Цели управления
Стабилизация угла прецессии:
.
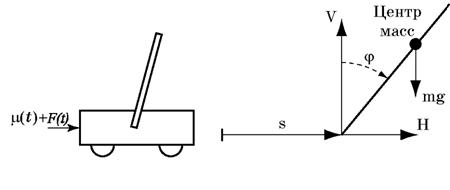
Задача 2. Механическая
система «перевернутый маятник на тележке»
|
Математическая модель
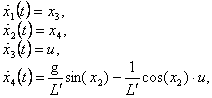
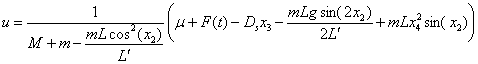
– горизонтальное
перемещение тележки;
– угловое отклонение
маятника от вертикального положения,
,
; т, L – масса маятника и расстояние между
осью и центром тяжести,
– момент инерции
относительно центра тяжести;
– масса тележки;
– эффективная длина
маятника;
– коэффициент трения;
– управляющая сила;
– возмущающая сила.
Переменные состояния:
,
,
,
.
Управляющие
воздействия:
Возмущающие
воздействия:
Параметры модели:
,
,
,
,
.
Цели управления:
Стабилизация маятника в вертикальном положении.
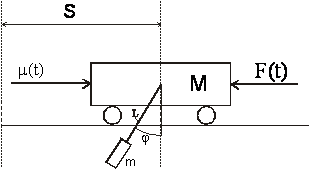
Задача
3. Двухмассовая
колебательная система
|
Математическая модель
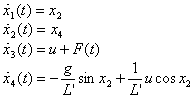
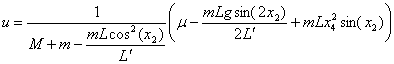
– горизонтальное
перемещение тележки;
– угловое отклонение
маятника от вертикального положения,
,
; т, L – масса маятника и расстояние между
осью и центром тяжести,
– момент инерции
относительно центра тяжести;
– масса тележки;
– эффективная длина
маятника;
– управляющая сила;
– возмущающая сила.
Переменные состояния:
,
,
,
.
Управляющие
воздействия:
.
Возмущающие
воздействия:
.
Параметры модели:
,
,
,
,
.
Цели управления:
Перемещение тележки в заданное положение.
Задача 4. Гирокомпас с гидравлическим успокоителем
Математическая модель
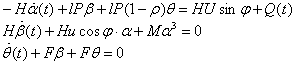
где
– угол поворота;
– угол подъема северного диаметра гиросферы над горизонтальной
плоскостью;
– угол наклона зеркала
жидкостного гидроуспокоителя над плоскостью экватора гидросферы; H – результирующий
собственный момент гироскопов в гиросфере;
– статический момент
гиросферы; U –
угловая скорость суточного вращения земного шара;
– широта места
наблюдения; F – запаздывание
в гидроуспокоителе;
– восстанавливающая сила;
– внешняя сила,
представляющая собой момент относительно восточного диаметра гиросферы,
накладываемого для ускоренного приведения гироскопа в меридиан.
где
Переменные состояния:
,
,
.
Управляющие
воздействия:
.
Возмущающие
воздействия:
и
.
Параметры модели:
;
;
;
;
;
.
Цели управления:
Приведение гирокомпаса в
меридиан:
.
Задача 5. Одноосный силовой гироскопический стабилизатор на неподвижном основании
|
Математическая модель
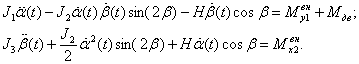
– угол поворота
наружной рамки относительно основания;
– угол отклонения оси ротора гироскопа от нормали к
плоскости наружной рамки (угол прецессии);
– кинетический момент
гироскопа;
– моменты инерции гиростабилизатора,
и
– моменты внешних сил,
приложенные к осям рамок,
– момент
стабилизирующего двигателя.
Переменные состояния:
,
,
,
.
Управляющие
воздействия:
Параметры модели:
;
;
;
.
Цели управления
Стабилизация угла прецессии:
.
Задача
6. Гидравлический рулевой привод
летательного аппарата
Математическая модель
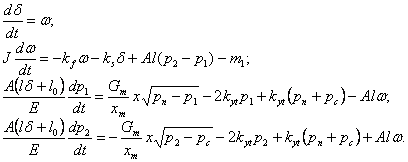
– положение руля;
– скорость изменения
положения руля;
– момент инерции руля;
– коэффициент момента
трения руля;
– коэффициент
шарнирного трения;
– рабочая площадь
поршня;
– длина рычага рулевого
привода;
– момент нагрузки, не
зависящий от положения руля,
– давления в I и II
областях силового гидроцилиндра,
– объемный модуль
упругости среды,
– нейтральное
положение золотника,
– коэффициент
пропорциональности между расходами утечек и перепадами давлений в корпусе
золотникового распределителя,
– максимальный расход
среды;
– максимальное по
модулю перемещение золотника,
– перемещение золотника;
– высокое давление
питающей магистрали;
– низкое давление
магистрали слива.
Переменные состояния:
,
,
,
.
Управляющие
воздействия:
.
Параметры модели:
,
,
,
,
,
,
,
,
,
,
,
,
.
Цели управления:
Поворот руля в заданное положение.
Задача
7. Вертолет в режиме висения
Математическая модель
– вертикальная
скорость;
– высота;
– шаг винта;
– аэродинамическая
сила сопротивления всегда направленная против вектора скорости;
– подъемная
сила винта;
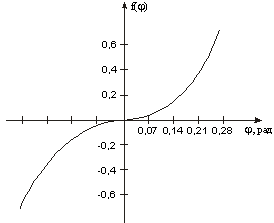
– нелинейная
зависимость (см. рисунок);
– аэродинамический
коэффициент;
– площадь винта;
– плотность воздуха на
уровне моря;
– коэффициент
запаса тяги по отношению к весу вертолета,
– вес вертолета;
– передаточное число
рулевого привода.
|
|
Переменные состояния:
,
,
.
Управляющие
воздействия:
.
Возмущающие
воздействия:
и
.
Параметры модели:
,
,
,
,
,
.
Цели управления:
Стабилизация высоты.
Задача 8. Надводное судно (стабилизация
курса при постоянной скорости хода, нулевом крене и постоянном дифференте)
|
Математическая модель
где
,
и
– проекции на оси
связанной системы координат вектора линейной скорости перемещения центра масс
судна и вектора угловой скорости вращения судна относительно центра масс;
– угол дрейфа;
,
,
– элементы матрицы
инерции твердого тела с учетом присоединенных масс жидкости;
и
– гидродинамические
коэффициенты;
– скорость хода;
– скоростной напор,
зависящий от плотности воды и скорости движения
,
– объемное
водоизмещение аппарата;
– угол перекладки вертикального
руля.
Переменные состояния:
,
,
.
Управляющие
воздействия:
.
Параметры модели:
|
11000 |
|
0,01 |
|
15000 |
|
0,03 |
|
120000 |
|
0,01 |
|
-0,01 |
|
1000 |
|
-0,02 |
|
10 |
|
-0,01 |
|
10000 |
,
,
,
,
,
,
,
,
,
Цели управления
Стабилизация угла рыскания.
Задача 9. Самолет (вывод на
заданную линию пути)
Математическая модель (боковое движение)
.
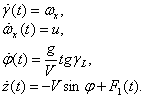
– угол крена самолета;
– угол курса самолета;
– боковое отклонение
самолета от оси взлетно-посадочной полосы;
– проекция вектора
угловой скорости на ось
связанной системы
координат;
– момент, создаваемый
элеронами;
– ограниченное значение
крена самолета;
– максимально возможное значение крена;
;
– внешнее
возмущение;
– постоянная скорость самолета;
– ускорение свободного
падения.
Переменные состояния:
,
,
,
.
Управляющие
воздействия:
.
Возмущающие
воздействия:
.
Параметры модели:
;
;
.
Цели управления:
Устранения бокового сноса
.
Задача 10. Летательный аппарат (режим снижения)
.
Математическая
модель
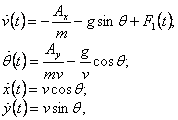
где
;
;
;
– скорость,
– угол между вектором скорости и местной горизонталью,
– дальность полета, отсчитываемая по поверхности
планеты,
– высота полета,
– ветровое возмущение;
– угол атаки.
Переменные состояния:
,
,
,
.
Управляющие
воздействия:
.
Возмущающие
воздействия:
.
Параметры модели:
;
;
;
;
;
;
.
Цели управления:
Выход на заданную высоту.
Задача
11. Летательный аппарат (движение в
горизонтальной плоскости)
Математическая модель
где:
– линейные продольная и боковая координаты центра масс
ЛА в горизонтальной плоскости;
– кривизна траектории;
– угол поворота траектории;
– скорость полета,
,
– соответственно продольная и боковая составляющие
скорости ветра.
Переменные состояния:
,
,
.
Управляющие
воздействия:
.
Возмущающие
воздействия:
,
.
Параметры модели:
.
Цели управления:
· Стабилизация курса
·
Движение по заданной траектории в горизонтальной
плоскости
.
12. Летательный аппарат (движение в
продольной плоскости)
Математическая модель
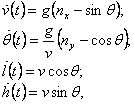
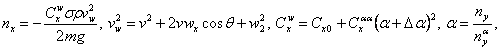
– скорость,
– угол наклона траектории,
– горизонтальная дальность,
– высота полета,
– продольная составляющая перегрузки,
– плотность воздуха,
– ускорение свободного падения,
– вертикальная составляющая перегрузки.
Переменные состояния:
,
,
.
Управляющие
воздействия:
.
Возмущающие
воздействия:
,
.
Параметры модели:
,
,
,
,
,
,
,
.
Цели управления:
Стабилизация высоты
Задача
13. Космический летательный аппарат
(вывод на заданную орбиту)
Математическая модель
где:
– радиус вращения;
;
– угол между линией, соединяющей центры КЛА и земли, и
горизонталью,
;
;
– управления в виде реактивных сил;
;
– постоянная всемирного тяготения;
.
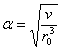Переменные состояния:
Управляющие
воздействия:
.
Возмущающие воздействия:
Параметры модели:
Цели управления:
Движение на заданной орбите с заданной угловой скоростью.
Задача 14. Орбитальный спутник
Математическая модель (в относительных единицах)
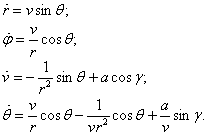
где:
– расстояние от центра Земли;
– полярный угол;
– скорость;
– угол между вектором
скорости и перпендикуляром к радиус-вектору;
– угол между вектором скорости и вектором тяги;
– реактивное ускорение.
Переменные состояния:
,
,
,
.
Управляющие
воздействия:
.
Цели управления:
Перевод на новую орбиту:
.
Задача
15. Электропривод с двигателем
постоянного тока последовательного возбуждения
|
Математическая
модель
,
,
,
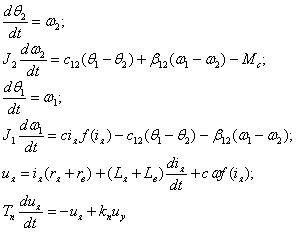
– угловые перемещения
и угловые скорости вала двигателя и исполнительного органа;
и
– моменты инерции вала
двигателя и исполнительного органа;
и
– коэффициенты
упругости и диссипации;
– напряжение на
обмотке якоря;
– ток якорной цепи;
и
– активные
сопротивления обмоток;
и
– индуктивность обмоток;
– конструктивная
постоянная двигателя;
– функция
намагничивания;
– коэффициент
намагничивания;
– момент сопротивления
нагрузки.
– коэффициент усиления преобразователя;
– постоянная времени
преобразователя.
Переменные состояния:
,
,
,
,
,
.
Управляющее
воздействие:
.
Номинальные данные и параметры модели (двигатель ДП-52):
Мощность, кВт |
33 |
Напряжение якоря, В |
220 |
Ток якоря, А |
175 |
Сопротивление обмотки якоря, Ом |
0,0545 |
Сопротивление обмотки возбуждения, Ом |
0,033 |
Индуктивность обмотки якоря, Гн |
0,0057 |
Индуктивность обмотки возбуждения, Гн |
0,0062 |
Конструктивная постоянная двигателя |
88,5 |
Поток полюса, мВб |
34 |
Статический коэффициент, кф |
0,00019 |
Частота вращения, рад/с |
66 |
Момент, Н м |
526 |
Момент инерции ротора, кг м2
|
1,87 |
Момент инерции ИО, кг м2 |
1 |
Коэффициент упругости, Н м/рад |
110 |
Коэффициент диссипации, Н м с/рад |
0,02 |
Коэффициент усиления преобразователя |
10 |
Постоянная времени преобразователя, с |
0,001 |
Цели управления
1) стабилизация угловой скорости исполнительного органа;
2) стабилизация углового положения исполнительного органа.
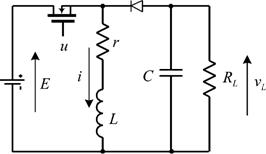
Задача 16. Повышающий преобразователь
На рисунке представлена принципиальная схема повышающего (Boost) преобразователя,
работающего на активно-реактивную
нагрузку. Статический
коэффициент передачи повышающего преобразователя равен
. На управление накладывается ограничение
.
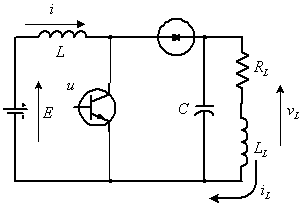
Параметры преобразователя:
Гн,
Ф,
Ом,
Гн.
В качестве источника входного напряжения используется система топливных элементов, имеющая следующую статическую характеристику:
,
где
В,
В,
м2,
Ом,
В,
,
.
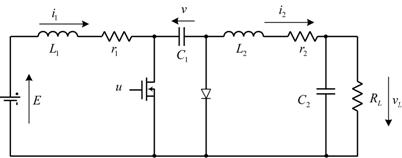
Задача 17. Повышающе–понижающий преобразователь
На рисунке приведена принципиальная схема
повышающе-понижающего преобразователя (Buck-Boost converter).
Статический коэффициент передачи повышающего преобразователя равен
. На управление накладывается ограничение
.
Параметры преобразователя:
Ом,
мкФ,
мкГн,
Ом,
В.
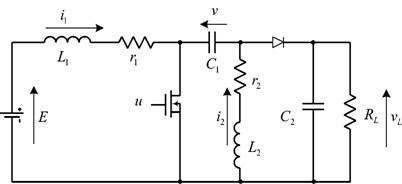
Задача 18. Повышающе–понижающий преобразователь Ćuk
Схема
Ćuk преобразователя
приведена на рисунке. Статический коэффициент передачи повышающего
преобразователя равен
. На управление накладывается ограничение
.
Параметры преобразователя:
Ом,
Гн,
Ом,
Гн,
Ф,
Ф,
Ом,
В.
Задача 19. Повышающе–понижающий преобразователь SEPIC
Схема SEPIC (Single-Ended Primary Inductance Converter) приведена на рисунке. Статический
коэффициент передачи повышающего преобразователя равен
. На управление накладывается ограничение
.
Параметры преобразователя:
Ом,
Гн,
Ом,
Гн,
Ф,
Ф,
Ом,
В.
Задача 20. Преобразователь Watkins–Johnson
Схема преобразователя приведена на рисунке. Статический
коэффициент передачи повышающего преобразователя равен
. На управление накладывается ограничение
.
Параметры преобразователя:
Ом,
Гн,
Ф,
Ом,
Гн,
В.
Задача 21. Обратный преобразователь Watkins–Johnson
Схема преобразователя приведена на рисунке. Статический
коэффициент передачи повышающего преобразователя равен
. На управление накладывается ограничение
.
Параметры преобразователя:
Ом,
Гн,
Ф,
Ом,
Гн,
В.