Модуль 4. Аналитическое конструирование динамических регуляторов с наблюдателями состояния

4.3. Адаптивное управление сборочными роботами с асинхронным электроприводом

Рассмотрим теперь решение важной прикладной задачи синергетического синтеза адаптивного регулятора для асинхронного электропривода (АЭП), который, конструктивно входит в состав сборочного робота. Для синтеза законов синергетического управления АЭП указанного назначения перепишем исходную модель АЭП с учетом изменения во времени момента инерции $J(t)$ и момента сопротивления $M_c(t)$ [111, 112]:
$$
\begin{split}
\frac{d \omega_r}{dt}&=\frac{mpk_r\psi_r i_{sy}-2M_c(t)-2\frac{dJ}{dt}\omega_r}{2J(t)};\\
\frac{d \psi_r}{dt}&=r_rk_r i_{sx}-\frac {1}{T_r} \psi_r;\\
\frac{d i_{sy}}{dt}&=-\frac{1}{{T_s}^*} i_{sy}-\omega_r i_{sx} -r_rk_r\frac{i_{sy}i_{sx}}{\psi_r}-\frac{k_r}{{L_s}^*}\omega_r\psi_r+\frac{1}{L_s^*}u_{sy};\\
\frac{d i_{sx}}{dt}&=-\frac{1}{{T_s}^*}i_{sx}+\omega_r i_{sy}+ r_r k_r\frac{i_{sy}^2}{\psi_r}+\frac{k_r}{T_r{L_s}^*}\psi_r+\frac{1}{L_s^*}u_{sx}.
\end{split}\qquad
(4.50)$$

Процедура построения синергетического регулятора зависит от характера изменения во времени момента инерции $J(t)$ и момента сопротивления $M_c(t)$. С помощью известных моделей возмущения можно построить расширенную модель синтеза и на ее основе методом АКАР найти законы управления $u_{sx}(\omega_r,\psi_r,i_{sy},i_{sx},\hat J,\hat M_c)$ и $u_{sy}(\omega_r,\psi_r,i_{sy},i_{sx},\hat J,\hat M_c)$, где $\hat J$ и $\hat M_c$ — оценки соответствующих величин.

С целью упрощения процедуры синтеза будем рассматривать декомпозированную систему, где управлениями являются токи $i_{sy}$, $i_{sx}$. Для этого введем параллельную совокупность макропеременных:
$$
\psi_1=i_{sy}-\varphi_1;\; \psi_2=i_{sx}-\varphi_2;\qquad
(4.51)$$
которые должны удовлетворять системе функциональных уравнений первого порядка типа (4.40).
При попадании ИТ системы (4.50) на пересечение многообразий $\psi_1{=}0$ и $\psi_2{=}0$, поведение объекта будет описываться редуцированной моделью:
$$
\begin{split}
\frac{d \omega_r}{dt}&=\frac{mpk_r\psi_r\varphi_1-2M_c(t)-2\dfrac{d J}{dt}\omega_r}{2J(t)};\\
\frac{d \psi_r}{dt}&=r_rk_r\varphi_2-\frac {1}{T_r}\psi_r,
\end{split}\qquad
(4.52)$$
где $\varphi_2, \varphi_2$ — внутренние управления, соответствующие токам $i_{sy}$, $i_{sx}$.

На следующем этапе синтеза необходимо найти такие законы управления $\varphi_1$, $\varphi_2$ для системы (4.52), которые обеспечивали бы выполнение заданных инвариантов и решали задачу адаптации к изменению моментов $J(t)$ и $M_c$. Как отмечалось выше, для системы управления АЭП можно ввести два инварианта: технологический $\omega_r=\omega_{r0}=const$ и электромагнитный $\psi_r=\psi_{r0}=const$. При решении задачи адаптации предполагается, что момент сопротивления $M_c=M_0=const$, а момент инерции изменяется по линейно-гармоническому закону
$$
J(t)=J_0+at+b\sin w_0t,\qquad
(4.53)$$
при этом коэффицинеты $a,b,w_0$ и $M_0$ могут принимать произвольные значения. На основе метода АКАР могут быть построены разные адаптивные регуляторы, которые подавляют внешние и внутренние возмущения в системе.

4.3.1. Синтез динамического регулятора для линейного возмущения

Сначала синтезируем динамический регулятор для ограниченной частоты $w_0$ гармонического воздействия (4.53). Если частота гармонического воздействия $w_0$ ограничена, то изменение момента инерции можно представить в виде линейной функции времени
$$
J(t)\cong J_0+at+bw_0t.\qquad
(4.54)$$
Соответствующие модели момента сопротивления $M_c=M_0=const$ и производной момента инерции $\dfrac{d J}{dt}\cong a+bw_0=const$, согласно идеологии синергетического синтеза, можно представить в виде двух интеграторов:
$$
\frac{d\nu_1}{dt}=\beta_1(\omega_r - \omega_{r0});\frac{d\nu_2}{dt}=\beta_2(\omega_r - \omega_{r0}),\qquad
(4.55)$$
где $\nu_1=\hat M_0$ — оценка момента сопротивления, $\nu_2=\hat a+\hat b\hat w_0$ — оценка приведенного момента инерции. Компенсация или подавление указанных возмущений осуществляется одновременно с регулированием выходной величины. Это означает, что после достижения заданной скорости вращения электропривода $\omega_r=\omega_{r0}$ оценки принимают значения, компенсирующие неизмеряемые возмущения. Если допустить, что оценки сходятся одновременно, т.е. при $\beta_1=\beta_2=\beta$, то тогда общую модель возмущений можно представить одним интегратором:
$$
\frac{d z}{dt}=\beta(\omega_r - \omega_{r0}),\qquad
(4.56)$$
где $z$ — оценка неизмеряемых постоянных величин $\{\hat M_0,\hat a+\hat b\hat w_0\}$.

Входное линейное воздействие (4.54) описывает линейно-гармонический закон (4.53) лишь в первом приближении, поэтому для подавления гармонического возмущения необходимо обеспечить существенно более высокую динамику переменной $z$ относительно изменения момента инерции в системе. Это условие можно записать как:
$$
2\pi\beta^2>>w_0.\qquad
(4.57)$$
При выполнении условия (4.57) расширенную модель синергетического синтеза на прересечении многообразий $\psi_1=0$ и $\psi_2=0$, в соответствии с (4.52) и (4.56), запишем в следующем виде:
$$
\begin{split}
&\frac{d \omega_r}{dt}=\frac{mpk_r\psi_r\varphi_1-2z}{2J_0};\\
&\frac{d \psi_r}{dt}=r_rk_r\varphi_2-\frac {1}{T_r}\psi_r; \\
&\frac{d z}{dt}=\beta(\omega_r - \omega_{r0}).
\end{split}\qquad
(4.58)$$
В знаменателе правой части первого уравнения системы (4.58) вместо $J(t)$ введено номинальное значение момента инерции $J_0$. Это возможно в силу того, что в (4.50) и (4.52) $J(t)$ отражает лишь инерционные свойства электропривода, и сама по себе не влияет на установившийся режим движения. Неточность в определении $J_0$ может повлиять только на время регулирования.

С использованием модели синергетического синтеза (4.58) найдем внутренние законы управления $\varphi_1(\omega_r,\psi_r,z)$ и $\varphi_2(\omega_r,\psi_r,z)$, подавляющие влияние внешних возмущений $J(t)$, $M_c$ и обеспечивающие устойчивость замкнутой системы. Для этого зададим желаемое изменение координат $\omega_r$ и $\psi_r$:
$$
\begin{split}
&\frac{d \omega_{r\textit{ж}}}{dt}=-\gamma_1\omega_{r\textit{ж}}-\gamma_2z_{\textit{ж}};\\
&\frac{d \psi_{r\textit{ж}}}{dt}=-\gamma_3(\psi_{r\textit{ж}}-\psi_{r0}),
\end{split}\qquad
(4.59)$$
где $\gamma_1,\gamma_2,\gamma_3$ — постоянные коэффициенты.

Для нахождения законов управления $\varphi_1(\omega_r,\psi_r,z)$ и $\varphi_2(\omega_r,\psi_r,z)$ приравняем выражения (4.bob-asin12} к соответствующим уравнениям из (4.59), в результате чего получим:
$$
\varphi_1=2\frac{(1-\gamma_2J_0)z-\gamma_1J_0\omega_r}{mpk_r\psi_r},\quad \varphi_2=\frac{\psi_r-T_r\gamma_3(\psi_r-\psi_{r0})}{T_rr_rk_r},\qquad
(4.60)$$
где $z=\beta\int(\omega_r-\omega_{r0})dt$.

Проведем исследование замкнутой декомпозированной модели синтеза (4.58), (4.60):
$$
\begin{split}
&\frac{d \omega_r}{dt}=-\gamma_1\omega_r-\gamma_2z;\\
&\frac{d \psi_r}{dt}=-\gamma_3(\psi_r-\psi_{r0});\\
&\frac{dz}{dt} = \beta(\omega_r - \omega_{r0}).
\end{split}\qquad
(4.61)$$

Очевидно, что при выполнении условия $\gamma_3>0$ решение второго уравнения модели (4.61) асимптотически устойчиво относительно желаемого состояния $\psi_r=\psi_{r0}$. Для анализа механической подсистемы первое и третье уравнение модели(4.61) преобразуем к виду:
$$
J_0\frac{d^2 \omega_r}{t^2}+\gamma_1\frac{d \omega_r}{dt}+\gamma_2\beta(\omega_r-\omega_{r0})=0.\qquad
(4.62)$$
Выбирая значения коэффициентов $\gamma_1>0$, $\gamma_2\beta>0$, можно обеспечить устойчивость уравнения (4.62) относительно состояния $\omega_r=\omega_{r0}$. Если в уравнении (4.62) ввести декремент затухания $\xi$, то можно найти соотношение между параметрами $\gamma_1=2\xi\sqrt{J_0\gamma_2\beta}$, которое задает требуемую колебательность механической подсистемы.

Рассмотрим поведение переменной $\omega_r$ при линейном изменении момента инерции (4.54) $J(t)\cong J_0+at+bw_0t$ и постоянном моменте сопротивления $M_c=M_0$ с учетом найденного управления $\varphi_1(\omega_r,\psi_r,z)$. Для этого подставим закон управления $\varphi_1(\omega_r,\psi_r,z)$ из (4.60) в первое уравнение (4.52):
$$
\frac{d \omega_r}{dt}=\frac{(1-\gamma_2J_0)z-\gamma_1J_0\omega_r-M_0-(a+bw_0)\omega_r}{J_0}.
$$
Дифференцируя последнее уравнение, получим:
$$
J_0\frac{d^2 \omega_r}{dt^2}+(\gamma_1J_0+a+bw_0)\frac{d \omega_r}{dt}+\beta(\omega_r-\omega_{r0})(\gamma_2J_0-1)=0.\qquad
$$
Данное уравнение, описывающее закон изменения скорости вращения, не зависит от величины момента сопротивления $M_0$, но на динамику переменной $\omega_r$ влияют параметры $a$, $b$, $w_0$ линейно-гармонического возмущения (4.54). Однако очевидно, что при $a,b,w_0>0$ поведение системы асимптотически устойчиво относительно состояния $\omega_r=\omega_{r0}$.

Процедура синтеза регулятора была выполнена для декомпозированной системы (4.52), где управлениями являются $\varphi_1$ и $\varphi_2$. Для получения физических управлений $u_{sx}$ и $u_{sy}$ необходимо подставить законы внутреннего управления $\varphi_1$ и $\varphi_2$ (4.60) в макропеременные (4.51) и решить функциональные уравнения (4.40) с учетом модели синергетического синтеза:
$$
\begin{split}
\frac{d \omega_r}{dt}&=\frac{mpk_r\psi_r i_{sy}-2z}{2J_0};\\
\frac{d \psi_r}{dt}&=r_rk_r i_{sx}-\frac {1}{T_r}\psi_r;\\
\frac{d i_{sy}}{dt}&=-\frac{1}{{T_s}^*}i_{sy}-\omega_r i_{sx}-r_rk_r\frac{i_{sy}i_{sx}}{\psi_r}-\frac{k_r}{{L_s}^*}\omega_r\psi_r+\frac{1}{L_s^*}u_{sy};\\
\frac{d i_{sx}}{dt}&=-\frac{1}{{T_s}^*}i_{sx}+\omega_r i_{sy}+r_rk_r\frac{i_{sy}^2}{\psi_r}+\frac{k_r}{T_r{L_s}^*}\psi_r+\frac{1}{L_s^*}u_{sx};\\
\frac{d z}{dt}&=(\omega_r- \omega_{r0})\beta.
\end{split}
$$
После выполнения аналитических преобразований законы управления принимают следующий вид:
$$
\begin{split}
u_{sx} &{=}\frac{L_s^*T_2\psi_r(T_r\gamma_3{-}1){-}T_r^2L_s^*\gamma_3(\psi_r{-}\psi_{r0}){+}T_r\psi_rL_s^*{-}r_rk_rT_r(\psi_rT_2{+}L_s^*i_{sx}T_r)}{T_2r_rk_rT_2^2}{+}\\
&+\frac{L_s^*i_{sx}(T_s^*+T_r)}{T_s^*T_r}+L_s^*(i_{sx}\gamma_3-i_{sy}\omega_r)+\frac{r_ri_{sy}^2L_s^*}{\psi_r};\\
u_{sy}&=\frac{2L_s^*\left(2(z-J_0(\gamma_1\omega_r+\gamma_2z))\beta T_r(\omega_r-\omega_{r0})(1-J_0\gamma_2)\right)}{mpk_r\psi_rT_r}+\\
&+L_s^*\frac{2J_0(\gamma_1\omega_r+\gamma_2z)+r_ri_{sx}(J_0(\gamma_1\omega_r+\gamma_2z)-2z)+4z(1-\gamma_3T_1)}{mpk_r\psi_rT_1}+\\
&+\omega_r(i_{sx}L_s^*+\psi_rk_r)+L_s^*\gamma_1i_{sy}+\frac{k_rr_ri_{sy}i_{sx}L_s^*}{\psi_r}+\frac{L_s^*i_{sx}(T_s^*-T_1)}{T_s^*T_1}.
\end{split}
(4.63)$$
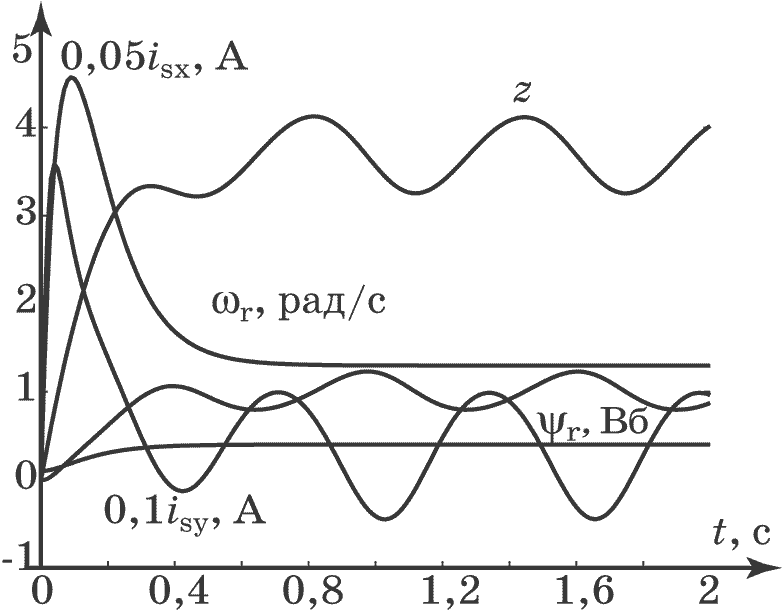
Проведем моделирование замкнутой системы (4.52), (4.56) с законами управления (4.63) при условии, что момент инерции $J(t)$ имеет гармонический характер (4.53), а момент сопротивления $M_c$ равен постоянной величине. На рис. 4.17, рис. 4.18, рис. 4.19 приведены графики моделирования замкнутой системы при следующих параметрах: $M_c=2$, $J_0=2$, $a=1$, $b=0,5$, $w_0=10$, $\omega_{r0}=1$, $\psi_{r0}=0,4$, $\xi=1$, $\beta=-10$, $\gamma_1=20,5$, $\gamma_2=-10$, $\gamma_3=10$, $T_1=T_2=0,1$. На рис. 4.20 приведены графики изменения отклонения $\varepsilon=\omega_r(t)-\omega_{r0}$ при разных соотношениях возмущения и параметров регулятора т.е. при $\beta^2=\lambda^2\dfrac{w_0}{2\pi}$ для $\lambda=\{10,50,100\}$, что позволяет проверить условие (4.57).

Рис. 4.17. Изменения координат

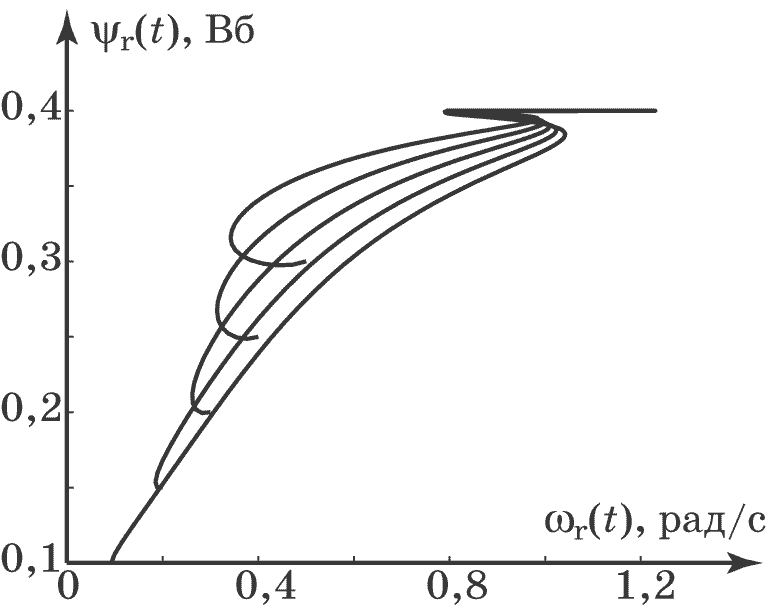
Рис. 4.18. Фазовый портрет системы

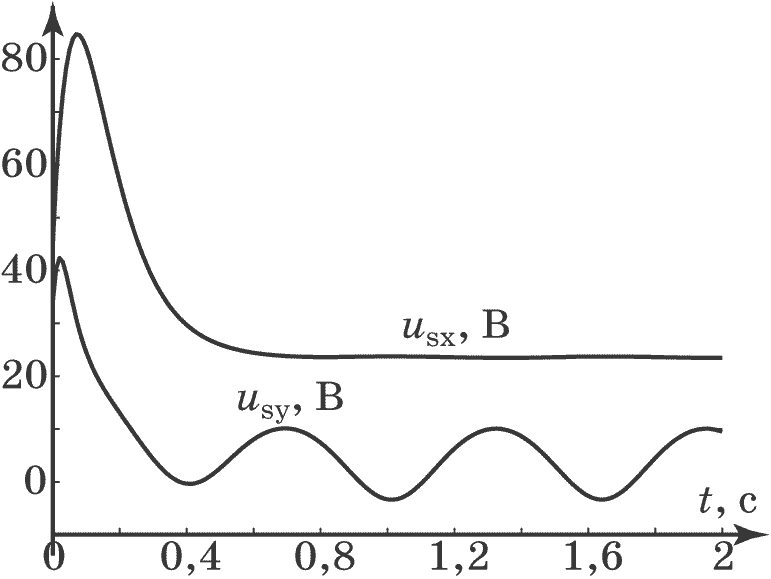
Рис. 4.19. Изменения управлений

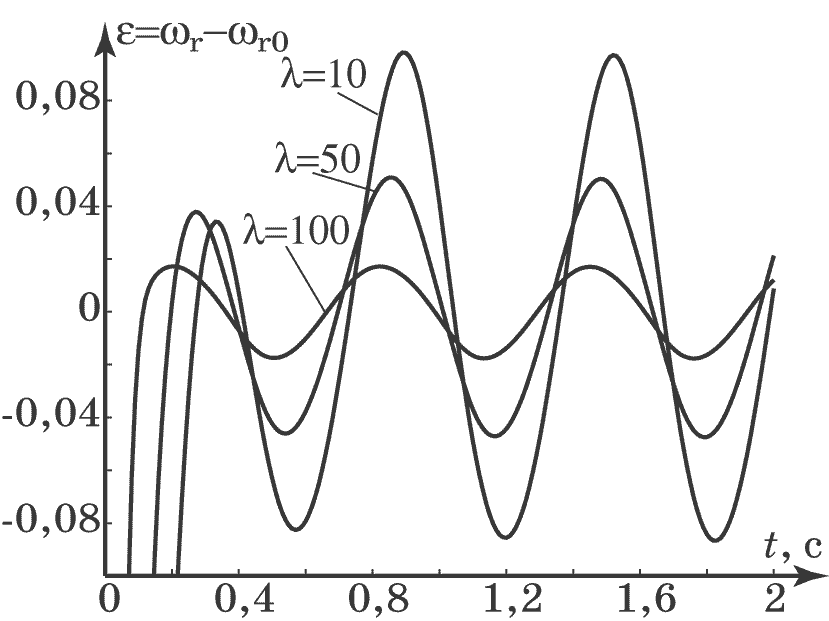
Рис. 4.20. Изменение отклонения

Приведенные результаты моделирования показывают, что синтезированный динамический регулятор отвечает поставленным требованиям по грубости системы к внешним возмущениям. В целом, как видно из графиков моделирования замкнутой системы, синтезированный динамический регулятор обеспечивает подавление как линейного возмущения, так и, допуская незначительную ошибку по выходной величине, гармонического воздействия, гарантируя асимптотическую устойчивость относительно заданного состояния $\omega_r=\omega_{r0}$, $\psi_r=\psi_{r0}$.

4.3.2. Синтез динамического регулятора для гармонического возмущения

Построим далее динамический регулятор, позволяющий полностью скомпенсировать линейно-гармоническое возмущение (4.57). Будем полагать, что момент сопротивления $M_c=M_0=const$, а производная момента инерции, согласно (4.57), равна $\dot J(t)=a+b\cos w_0t$. Для полного “подавления” гармонического возмущения необходимо иметь информацию о значении частоты гармонического воздействия $w_0$, в противном случае компенсация будет частичная. Тогда математические модели моментов сопротивления и инерции при условии одновременной компенсации постоянной составляющей будут иметь вид:
$$
\begin{split}
\frac{d z_1}{dt}&=(\omega_{r0}-\omega_r)\beta;\\
\frac{d z_2}{dt}&=z_3+z_1;\\
\frac{d z_3}{dt}&=-w_0^2z_2,
\end{split}\qquad
(4.64)$$
где $z_1$ — оценка постоянного возмущения, $z_2,z_3$ — оценки гармонического возмущения. При достижении электроприводом заданной скорости вращения $\omega_r=\omega_{r0}$, указанные выше возмущения, соответствующие модели (4.64), подавляются. Для синтеза законов синергетического синтеза составим на основе (4.50) и модели (4.64) расширенную модель синтеза:
$$
\begin{split}
\frac{d \omega_r}{dt}&=\frac{mpk_r\psi_ri_{sy}-2z_1-2z_2\omega_r}{2J_0};\\
\frac{d \psi_r}{dt}&=r_rk_ri_{sx}-\frac {1}{T_r}\psi_r;\\
\frac{d i_{sy}}{dt}&=-\frac{1}{T_s^*}i_{sy}-\omega_ri_{sx}-r_rk_r\frac{i_{sy}i_{sx}}{\psi_r}-\frac{k_r}{L_s^*}\omega_r\psi_r+\frac{1}{L_s^*}u_{sy};\\
\frac{d i_{sx}}{dt}&=-\frac{1}{T_s^*}i_{sx}+\omega_ri_{sy}+r_rk_r\frac{i_{sy}^2}{\psi_r}+\frac{k_r}{T_rL_s^*}\psi_r+\frac{1}{L_s^*}u_{sx};\\
\frac{d z_1}{dt}&=(\omega_{r0}-\omega_r)\beta;\\
\frac{d z_2}{dt}&=z_3+z_1;\\
\frac{d z_3}{dt}&=-w_0^2z_2.
\end{split}\qquad
(4.65)$$
Модель (4.65) позволяет синтезировать законы управления $u_{sx}$ и $u_{sy}$, которые совместно с моделью возмущений (4.64) обеспечивают подавление неизмеряемого возмущения (4.57) и $M_0$.

Аналогично приведенной выше процедуре синтеза на первом этапе вводим совокупность макропеременных (4.51), удовлетворяющую решению системы функциональных уравнений (4.40). Тогда при попадании ИТ системы в окурестность пересечения многообразий $\psi_1=0$ и $\psi_2=0$ ее поведение будет описываться декомпозированной моделью
$$
\begin{split}
\frac{d \omega_r}{dt}&=\frac{mpk_r\psi_r\varphi_1-2z_1-2z_2\omega_r}{2J_0};\\
\frac{d \psi_r}{dt}&=r_rk_r\varphi_2-\frac {1}{T_r}\psi_r;\\
\frac{d z_1}{dt}&=(\omega_{r0}-\omega_r)\beta;\\
\frac{d z_2}{dt}&=z_3+z_1;\\
\frac{d z_3}{dt}&=-w_0^2z_2.
\end{split}
(4.66)$$
Внутреннее управляющее воздействие $\varphi_2$, согласно вышеприведенной методике, соответствует второму выражению в (4.60). Для нахождения управления $\varphi_1$ введем макропеременную
$$
\psi_3=\beta(\omega_r - \omega_{r0}) - \varphi_3.\qquad
(4.67)$$
Тогда на втором этапе декомпозиции поведение системы будет описываться следующей моделью:
$$
\begin{split}
\frac{d z_1}{dt}&=\varphi_3;\\
\frac{d z_2}{dt}&=z_3+z_1;\\
\frac{d z_3}{dt}&=-w_0^2z_2.
\end{split}\qquad
(4.68)$$
Для определения внутреннего управления $\varphi_3$ введем макропеременную
$$
\psi_4=z_1 + \lambda z_2,\qquad
(4.69)$$
удовлетворяющую решению функционального уравнения
$$
T_4 \frac{d \psi_4}{dt}+\psi_4=0.\qquad
(4.70)$$
После совместного решения (4.69) и (4.70) с учетом декомпозированной модели (4.68) находим
$$
\varphi_3=-\lambda (z_1 + z_3) - \frac{z_1+\lambda z_2}{T_4}.\qquad
(4.71)$$
Условие устойчивости движения и колебательность на конечном многообразии $\psi_4=0$ получим из уравнения:
$$
\ddot z_{2\psi_4}(t)+\lambda\dot z_{2\psi_4}(t)+w_0^2z_{2\psi_4}=0.
$$
Если в последнем уравнении положить декремент затухания равным единице, то тогда $\lambda=2w_0$.
Подставив макропеременную (4.67) в функциональное уравнение
$$
T_3 \frac{d \psi_3}{dt}+\psi_3=0
$$
и учтя выражение (4.71) и декомпозированную модель (4.66), определим вид внутреннего управления $\varphi_1$:
$$
\begin{split}
\varphi_1=\frac{2J_0}{\beta mpk_r\psi_r}\left [\beta(\omega_{r0}-\omega_r)\left(\lambda - \frac{1}{T_3}-\frac{1}{T_4}\right) + \lambda(z_1+z_3)\left(\frac{1}{T_4}-\frac{1}{T_3}\right) + \right.\\
+\left. z_1\left(\frac{\beta}{J_0}-\frac{1}{T_3T_4}\right) - z_2\left(\frac{\lambda}{T_3T_4}+\lambda w_0^2-\frac{\beta}{J_0}\omega_r\right)\right].
\end{split}\qquad
(4.72)$$
После выполнения аналитических вычислений законы внешнего управления будут иметь вид:
$$
\begin{split}
u_{sx}&{=}\frac{L_s^*T_2\psi_r(T_r\gamma_3{-}1){-}T_r^2L_s^*\gamma_3(\psi_r{-}\psi_{r0}){+}T_r\psi_rL_s^*{-}r_rk_rT_r(\psi_rT_2{+}L_s^*i_{sx}T_r)}{T_2r_rk_rT_2^2}{+}\\
&+\frac{L_s^*i_{sx}(T_s^*+T_r)}{T_s^*T_r}+L_s^*(i_{sx}\gamma_3-i_{sy}\omega_r)+\frac{r_ri_{sy}^2L_s^*}{\psi_r};
\end{split}\qquad
(4.73)$$
$$
\begin{split}
u_{sy}&=\frac{2L_s^*r_ri_{sx}(J_0\lambda(\omega_r-\omega_{r0})-\beta(z_1-z_3\omega_r)-J_0\lambda w_0^2z_2)}{\beta mp\omega_r^2}+\\
&\frac{2J_0L_s^*r_ri_{sx}(\beta(T_3+T_4)(\omega_r-\omega_{r0})+(1+\lambda(T_3+T_4))(\lambda_7+z_1))}{T_3T_4\beta_mp\psi_r^2}-\\
&\frac{2J_0L_s^*(\lambda z_2+z_1+\lambda(z_1+z_3)(T_r+T_3+T_4))}{T_3T_4\beta mpk_rT_r\psi_r}+\frac{k_rr_ri_{sy}i_{sx}L_s^*}{\psi_r}+\\
&\frac{2L_s^*((z_1+z_3\omega_r)(T_3+T_4)-J_0(1+\lambda(T_3+T_4))(\omega_r-\omega_{r0}))}{T_3T_4mpk_r\psi_r}-\\
&\frac{2J_0L_s^*(\lambda z_2{+}z_1{+}\lambda(z_1{+}z_3)(T_3{+}T_4){+}\beta(T_3T_4\lambda{+}(T_3{+}T_4)(\omega_r{-}\omega_{r0})))}{T_1T_3T_4\beta mpk_r\psi_r}.
\end{split}\qquad
(4.74)$$

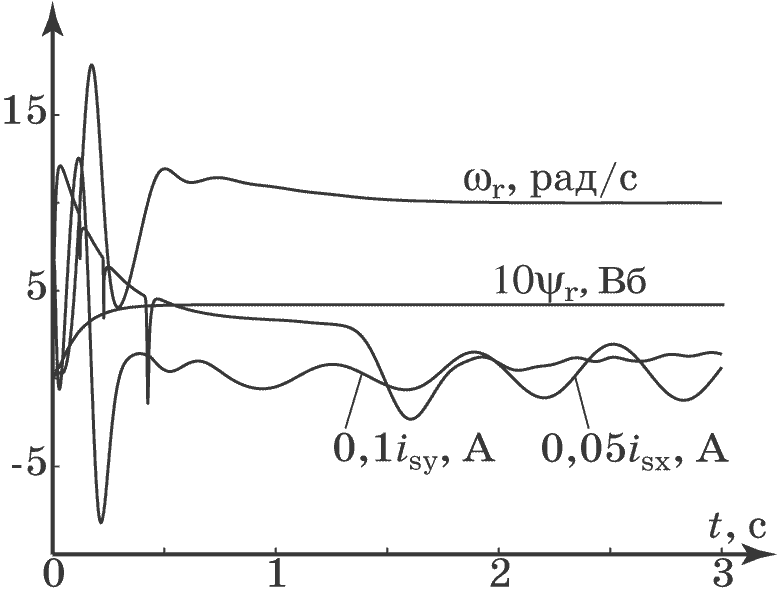
На рис. 4.21, рис. 4.22, рис. 4.23, рис. 4.24 приведены графики моделирования замкнутой системы (4.50), (4.64), (4.73), (4.74) при следующих параметрах: $M_c=2$, $J_0=2$, $a=1$, $b=0,5$, $w_0=1$, $\omega_{r0}=10$, $\psi_{r0}=0,4$, $\xi=1$, $\beta=-10$, $\gamma_3=10$, $T_1=T_2=0,01$, $T_3=T_4=0,1$.

Рис. 4.21. Изменения координат

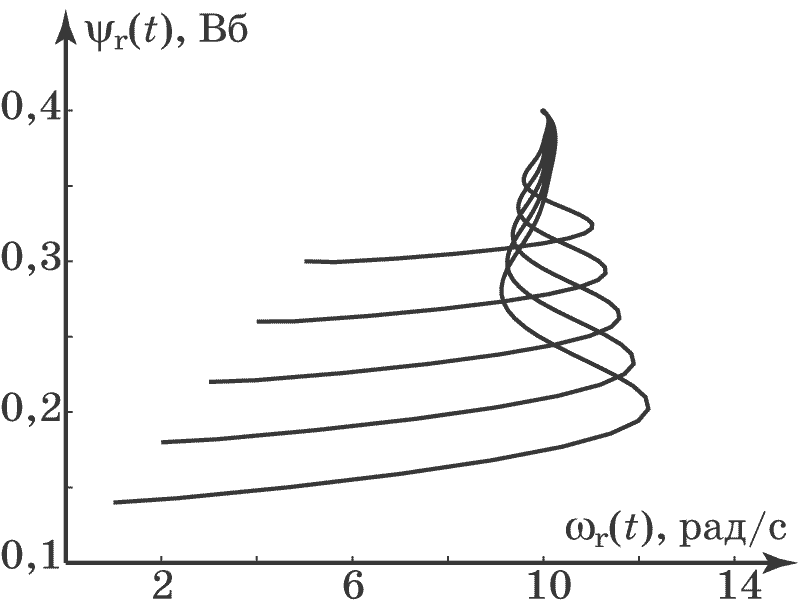
Рис. 4.22. Фазовый портрет системы

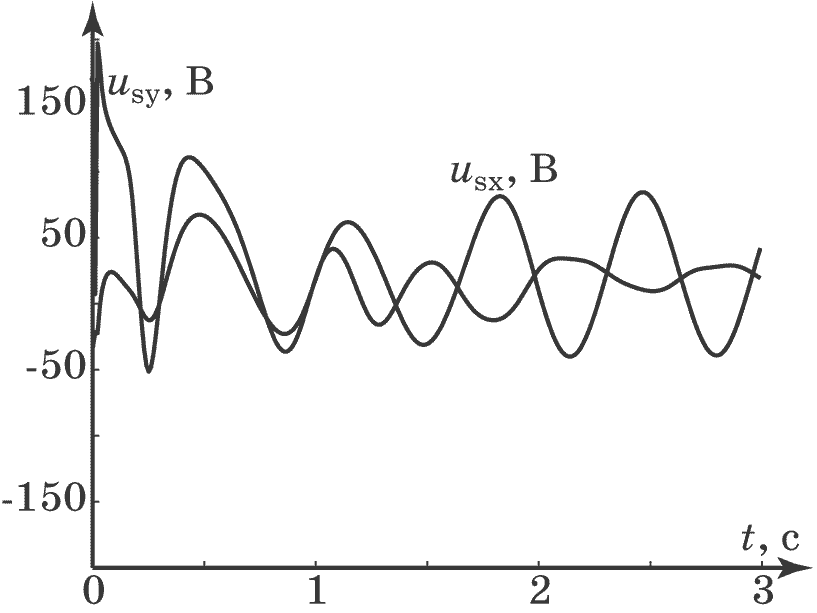
Рис. 4.23. Изменения управлений

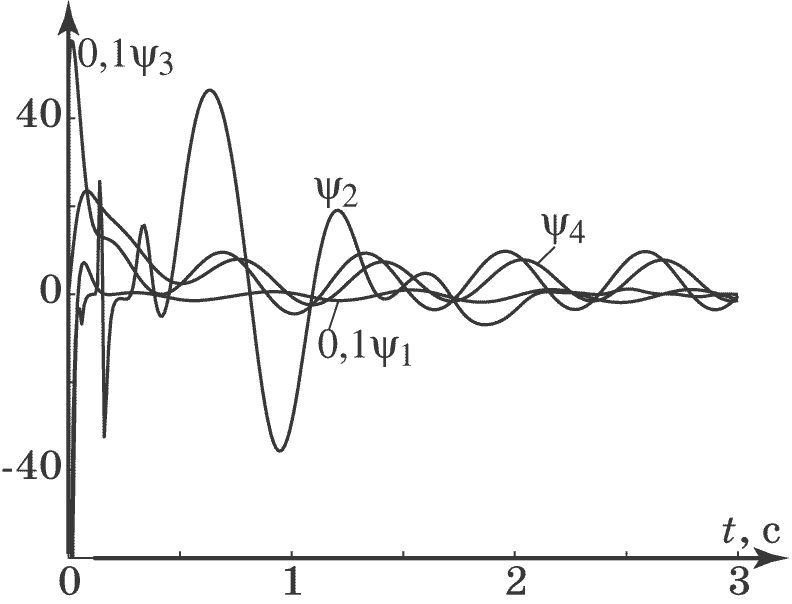
Рис. 4.24. Изменения макропеременных

Судя по результатам моделирования (рис. 4.21, рис. 4.22, рис. 4.23, рис. 4.24), регулятор (4.64), (4.73), (4.74) отвечает поставленным требованиям, обеспечивает приемлемое время регулирования и точность. Синтезированный регулятор (4.64), (4.73), (4.74) получен на основе использования модели синергетического синтеза (4.65), учитывающей гармонический характер изменения момента инерции и кусочно-постоянное воздействие момента сопротивления, по сравнению с законом управления (4.63) более успешно подавляет действующие на объект (4.50) данного типа возмущения.

4.3.3. Синтез адаптивного регулятора с наблюдателями возмущений

Построим адаптивный синергетический регулятор, обеспечивающий стабилизацию скорости вращения $\omega_r=\omega_{r0}$ и потокосцепления $\psi_r=\psi_{r0}$ с наблюдателями момента инерции, изменяющегося по гармоническому закону \mathbfox{$J(t)=J_0+at+b\sin w_0t$}, и момента сопротивления, который принимает постоянное значение $M_c=M_0$. Для построения наблюдателей введем модели указанных возмущений $J(t)$ и $M_c(t)$, т.е.
$$
\frac{d\nu_1}{dt}=\nu_2,\,
\frac{d\nu_2}{dt}=-w_0^2\nu_1,\,
\frac{d J}{dt}=\nu_2,\,
\frac{d\nu_3}{dt}=0,\,
M_c=\nu_3.
$$
На основе этих моделей возмущений можно построить расширенную модель синтеза системы:
$$
\begin{split}
\frac{d \omega_r}{dt}&=\frac{mpk_r\psi_ri_{sy}-2\nu_3-2\nu_2\omega_r}{2J_0};\\
\frac{d \psi_r}{dt}&=r_rk_ri_{sx}-\frac {1}{T_r}\psi_r;\\
\frac{d i_{sy}}{dt}&=-\frac{1}{{T_s}^*}i_{sy}-\omega_ri_{sx}-r_rk_r\frac{i_{sy}i_{sx}}{\psi_r}-\frac{k_r}{{L_s}^*}\omega_r\psi_r+\frac{1}{L_s^*}u_{sy};\\
\frac{d i_{sx}}{dt}&=-\frac{1}{{T_s}^*}i_{sx}+\omega_ri_{sy}+r_rk_r\frac{i_{sy}^2}{\psi_r}+\frac{k_r}{T_r{L_s}^*}\psi_r+\frac{1}{L_s^*}u_{sx};\\
\frac{d\nu_1}{dt}&=\nu_2;\\
\frac{d\nu_2}{dt}&=-w_0^2\nu_1;\\
\frac{d\nu_3}{dt}&=0.
\end{split}\qquad
(4.75)$$
Особенность приведенной модели синтеза (4.75) заключается в более точном, по сравнению с (4.65), описании возмущений данного класса, что, соответственно, улучшает показатели оценивания.
В соответствии с макропеременными (4.51) и функциональными уравнениями (4.40) декомпозируем модель (4.75), в результате чего получим:
$$
\begin{split}
\frac{d \omega_r}{dt}&=\frac{mpk_r\psi_r\varphi_1-2\nu_3-2\nu_2\omega_r}{2J_0};\\
\frac{d \psi_r}{dt}&=r_rk_r\varphi_2-\frac {1}{T_r}\psi_r;\\
\frac{d\nu_1}{dt}&=\nu_2;\\
\frac{d\nu_2}{dt}&=-w_0^2\nu_1;\\
\frac{d\nu_3}{dt}&=0.
\end{split}\qquad
(4.76)$$

С целью стабилизации скорости и потокосцепления введем для системы (4.76) следующую совокупность макропеременных:
$$
\psi_3=\omega_r-\omega_{r0};\; \psi_4=\psi_r-\psi_{r0},\qquad
(4.77)$$
которые должны удовлетворять уравнениям первого порядка
$$
T_3\frac{d\psi_3}{dt}+\psi_3=0;\; T_4\frac{d\psi_4}{dt}+\psi_4=0.\qquad
(4.78)$$
Согласно [61], для построения наблюдателя переменных $\nu_1$, $\nu_2$ и $\nu_3$ сформируем вектор макропеременных:
$$
\boldsymbol\Psi=
\begin{bmatrix}
&\nu_1-\hat\nu_1 \\
&\nu_2-\hat\nu_2 \\
&\nu_3-\hat\nu_3
\end{bmatrix},\qquad
(4.79)$$
изменение которого во времени должно подчиняться дифференциальным уравнениям
$$
\frac{d\boldsymbol\Psi}{dt}-\mathbf L\boldsymbol\Psi=0\qquad
(4.80)$$
где $\mathbf L=\|l_{ij}\|$ — матрица, определяющая устойчивость этих уравнений. Уравнения (4.80) в развернутом форме, после замены переменной $\nu_3=\dfrac{m}{2}pk_r\psi_r\varphi_1-\nu_2\omega_r-\dfrac{d \omega_r}{dt}J_0$, будут иметь вид:
$$
\begin{split}
&\nu_2{-}\frac{d{\hat\nu}_1}{dt}{-}l_{11}(\nu_1{-}\hat\nu_1){-}l_{12}(\nu_2{-}\hat\nu_2){-}l_{13}\left(\frac{m}{2}pk_r\psi_r\varphi_1{-}\nu_2\omega_r{-}\frac{d \omega_r}{dt}J_0{-}\hat\nu_3\right){=}0; \\
&{-}w_0^2\nu_1{-}\frac{d{\hat\nu}_2}{dt}{-}l_{21}(\nu_1{-}\hat\nu_1){-}l_{22}(\nu_2{-}\hat\nu_2){-}l_{23}\hspace{-1mm}\left(\hspace{-1mm}\frac{m}{2}pk_r\psi_r\varphi_1{-}\nu_2\omega_r{-}\frac{d \omega_r}{dt}J_0{-}\hat\nu_3\hspace{-1mm}\right)\hspace{-1mm}{=}0; \\
&{-}\frac{d{\hat\nu}_3}{dt}{-}l_{31}(\nu_1{-}\hat\nu_1){-}l_{32}(\nu_2{-}\hat\nu_2){-}l_{33}\left(\frac{m}{2}pk_r\psi_r\varphi_1{-}\nu_2\omega_r{-}\frac{d \omega_r}{dt}J_0{-}\hat\nu_3\right){=}0.
\end{split}\qquad
(4.81)$$

Для построения уравнений наблюдателя сначала необходимо исключить ненаблюдаемые координаты путем задания соответствующих значений элементов матрицы $\mathbf L$:
$$
l_{11}=0,\; l_{12}=1+l_{13}\omega_r,\; l_{21}=-w_0^2,\; l_{22}=l_{23}\omega_r,\; l_{31}=0,\; l_{32}=l_{33}\omega_r.\qquad
(4.82)$$
Далее, путем выбора оставшихся трех элементов $l_{13},l_{23}$ и $l_{33}$, необходимо задать динамику наблюдателя путем выбора характеристического полинома матрицы $\mathbf L$, который с учетом уже выбранных элементов $l_{ij}$ (4.82) запишется в виде:
$$
\begin{split}
\det(p\mathbf E-\mathbf L)=&
\begin{bmatrix}
& p & -1-l_{13}\omega_r & -l_{13} \\
& w_0^2 & p-l_{23}\omega_r & -l_{23} \\
& 0 & -l_{33}\omega_r & p-l_{33}
\end{bmatrix}=\\
&=p^3-(l_{33}+l_{23}\omega_r)p^2+(w_0^2l_{13}\omega_r+w_0^2)p+w_0l_{33}.
\end{split}
$$
Выберем желаемый полином так, чтобы в уравнениях наблюдателя не появилось деления на переменную $\omega_r$:
$$
\begin{split}
\Lambda&=(p^2+w_0^2\omega_r^2\lambda_1p+w_0^2)(p+\omega_r^2\lambda_2)=\\
&=p^3-(w_0^2\omega_r^2\lambda_1+\omega_r^2\lambda_2 )p^2+(w_0^2+w_0^2\omega_r^4\lambda_1\lambda_2)p-w_0^2\omega_r^2\lambda_2,
\end{split}
$$
где $\lambda_1,\lambda_2$— некоторые положительные числа, задающие динамику наблюдателя. Последнее уравнение обладает решениями
$$
p_{1,2}=-\frac{1}{2}\omega_r^2\lambda_1w_0^2\pm\frac{w_0}{2}\sqrt{\omega_r^4w_0^2\lambda_1^2-4},\quad p_3=-\omega_r^2\lambda_2,
$$
которые имеют отрицательную вещественную часть при любых положительных значениях $\lambda_1$ и $\lambda_2$. Сопоставляя желаемый полином с характеристическим полиномом матрицы $\mathbf L$, найдем элементы $l_{13},l_{23}$ и $l_{33}$:
$$
l_{13}=\omega_r^3\lambda_1\lambda_2,l_{23}=-\omega_rw_0^2\lambda_1,l_{33}=-\omega_r^2\lambda_2.\qquad
(4.83)$$
После выбора элементов (4.82), (4.83) произведем редуцирование уравнений наблюдателя (4.81), т.е. произведем замену переменных для исключения производной от координаты $\omega_r$:
$$
z_1=\hat\nu_1-\frac{J_0\lambda_1\lambda_2\omega_r^4}{4}, \,\, z_2=\hat\nu_2+\frac{J_0w_0^2\lambda_1\omega_r^2}{2},\,\, z_3=\hat\nu_3+\frac{J_0\lambda_2\omega_r^3}{3}.
$$
В результате уравнения наблюдателя для координат $\nu_1,\nu_2$ и $\nu_3$ будут иметь вид:
$$
\begin{split}
\frac{d z_1}{dt}&=(1{-}\omega_r^4\lambda_1\lambda_2)\left(z_2{-}\frac{J_0w_0^2\lambda_1\omega_r^2}{2}\right){-}\omega_r^3\lambda_1\lambda_2\left(k_m\psi_r{-}z_3+\frac{J_0\lambda_2\omega_r^3}{3}\right){=}0; \\
\frac{d z_2}{dt}&=-w_0^2\left(z_1+\frac{J_0\lambda_1\lambda_2\omega_r^4}{4}\right)-w_0^2\omega_r^2\lambda_1\left(z_2-\frac{J_0w_0^2\lambda_1\omega_r^2}{2}\right)+\\
&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+\omega_rw_0^2\lambda_1\left(k_m\psi_r-z_3+\frac{J_0\lambda_2\omega_r^3}{3}\right)=0; \\
\frac{d z_3}{dt}&=-\omega_r^3\lambda_2\left(z_2-\frac{J_0w_0^2\lambda_1\omega_r^2}{2}\right)+\omega_r^2\lambda_2\left(k_m\psi_r-z_3+\frac{J_0\lambda_2\omega_r^3}{3}\right)=0; \\
\hat\nu_1&=z_1+\frac{J_0\lambda_1\lambda_2\omega_r^4}{4}; \quad
\hat\nu_2=z_2-\frac{J_0w_0^2\lambda_1\omega_r^2}{2}; \quad
\hat\nu_3=z_3-\frac{J_0\lambda_2\omega_r^3}{3};
\end{split}\qquad
(4.84)$$

Синергетические законы управления и для расширенной модели (4.75) получаются путем совместного решения уравнений (4.51), (4.77), (4.78) и систем (4.75), (4.76).

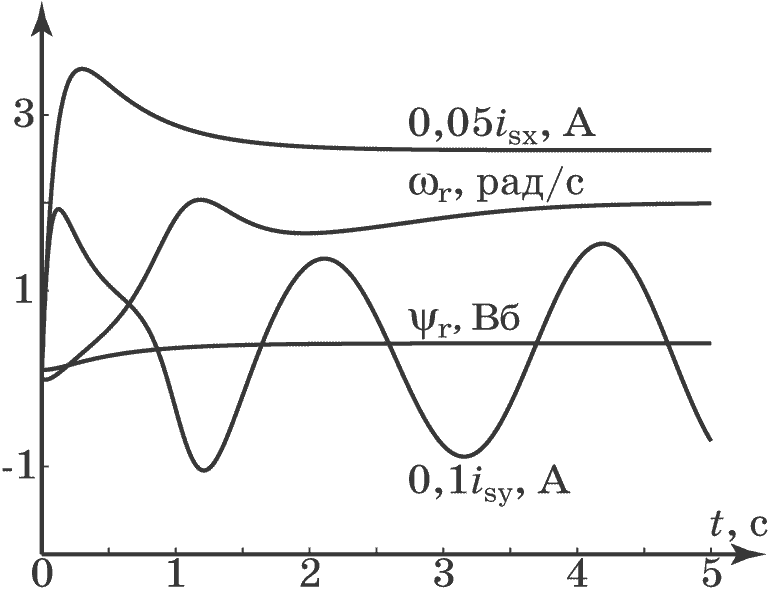
Результаты моделирование электропривода (4.50) с наблюдателями возмущений (4.84) приведены на рис. 4.25, рис. 4.26, рис. 4.27, рис. 4.28. Моделирование проводилось при следующих параметрах регулятора $\lambda_1=0,2$, $\lambda_2=1$, $T_1=T_2=0,1$, $T_3=T_4=0,5$, $\omega_{r0}=2$, $\psi_{r0}^0=0,4$ и объекта $M_c=2$, $a=0$, $b=1,5$, $w_0=3$.

Рис. 4.25. Изменения координат

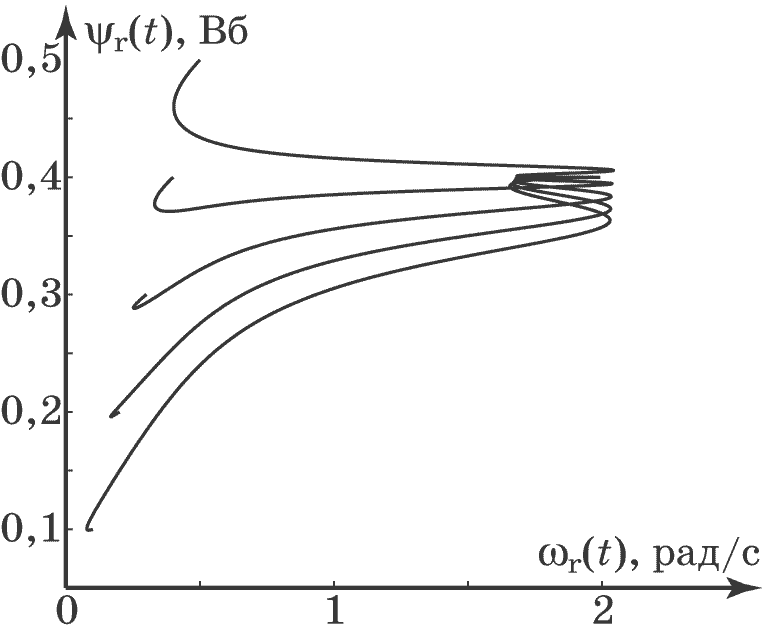
Рис. 4.26. Фазовый портрет системы

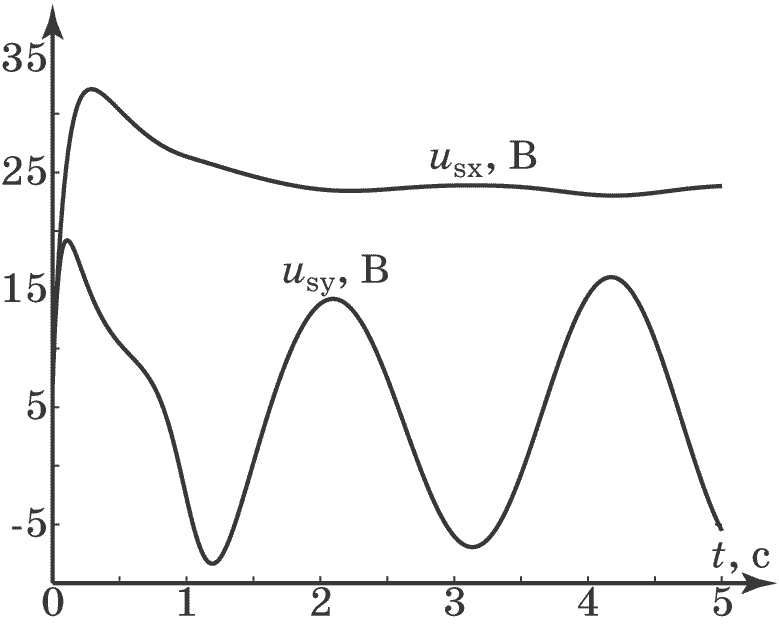
Рис. 4.27. Изменения управлений

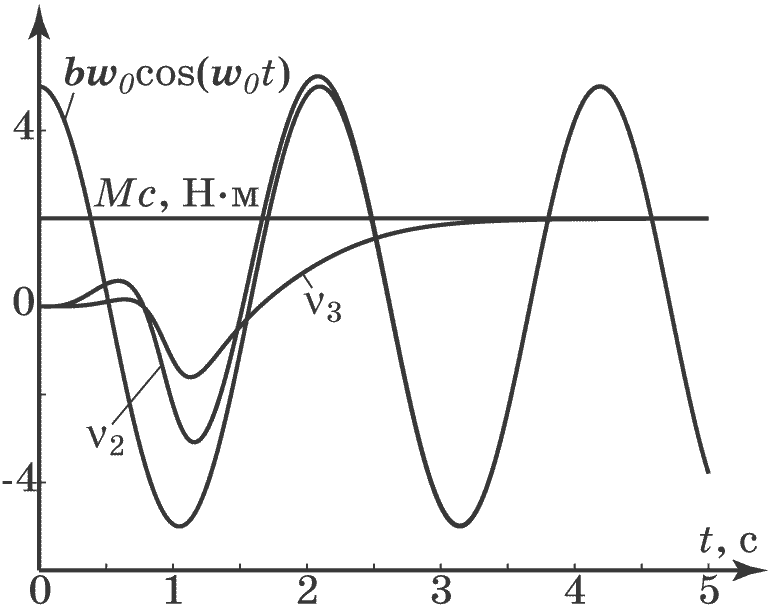
Рис. 4.28. Графики возмущений и их оценок

Результаты моделирования показывают, что синтезированный методом АКАР адаптивный регулятор отслеживает изменение неизмеряемых возмущений и обеспечивает устойчивую стабилизацию выходных координат системы.

Итак, синергетический регулятор успешно решает задачу управления сборочным роботом в условиях значительной параметрической неопределенности и действия внешних возмущений.