Модуль 4. Аналитическое конструирование динамических регуляторов с наблюдателями состояния

4.2. Адаптивное управление сборочными роботами с электроприводом постоянного тока

Рассмотрим сначала решение синергетическим методом задачи управления электроприводами сборочных роботов с ангулярными кинематическими схемами. В монографии [61, 59] подробно рассматривается задача управления такими роботами на основе технологии ассоциативной памяти, в состав которой входит классификатор состояния объекта и формирователь управлений, необходимые для идентификации текущих параметров объекта и формирования вектора настраиваемых параметров закона управления.

4.2.1. Модель электропривода

Аналитическое описание рассматриваемых механических объектов — ангулярных роботов может осуществляться путем учета структуры математических моделей механических процессов, протекающих в подсистемах и нахождение связей между этими процессами. Задача синтеза в данном случае должна включать процедуру построения адаптивного регулятора, который оценивает параметры моделей механических подсистем и компенсировать внешнее возмущение [61, 59]. Наиболее общей процедурой построения моделей ангулярных систем является методика нахождения уравнений Лагранжа второго рода. В данном случае рассматривается ангулярная система, включающая $n$ исполнительных приводов, с помощью которых достигается заданная цель управления. Считается, что моменты инерции приведены к валу каждого электропривода и, следовательно, зависят от кинематической схемы системы, т.е. $J_i=J_i(\varphi_1,\varphi_2 \dots \varphi_n), i=1..n$, где $\varphi_i$ — угол поворота вала $i$-го электропривода. Для построения математической модели данной механической системы рассмотрим уравнения Лагранжа для голономной многомассовой динамической системы:
$$
\frac{d}{dt}\frac{\partial W_k}{\partial \omega_i}-\frac{\partial W_k}{\partial \varphi_i}=-\frac{\partial Q}{\partial \omega_i}-\frac{\partial W_p}{\partial \varphi_i}+M(\omega_i,\varphi_i), i=i..n,\qquad
(4.20)$$
где $W_k$ и $W_p$ — кинетическая и потенциальная энергии системы; $\omega_i$ — угловая скорость $i$-го привода; $Q$ — диссипативная функция, характеризующая момент сопротивления $M_c$, вызванный диссипативными силами в упругих элементах (внутренним вязким трением).

Поскольку рассматривается ангулярная система, то кинетическая энергию такой системы можно записать в виде выражения:
$$
W_k=\sum\limits_{i=1}^n{\frac{J_i(\varphi_1,\varphi_2 \dots \varphi_n)\omega_i^2}{2}}.\qquad
(4.21)$$
При анализе поведения системы будет рассматриваться $i$-й привод и учитываться влияние на него других приводов. Уравнение описывающее функционирование $i$-го привода в соответствии с (4.Ur_Lagr} и (4.Kin_En} запишется в следующем виде:
$$
\begin{split}
&J_i(\varphi_1,\varphi_2 \dots \varphi_n)\frac{\omega_i}{dt}{+}\omega_i\sum\limits_{k=1,k\neq i}^n{\frac{\partial J_i(\varphi_1,\varphi_2 \dots \varphi_n)}{\partial \varphi_k}\omega_k}{+}\frac{1}{2}\frac{\partial J_i(\varphi_1,\varphi_2 \dots \varphi_n)}{\partial \varphi_i}\omega_i^2=\\
&=-M_c-M_u+M(\omega_i,\varphi_i).
\end{split}\qquad
(4.22)$$
Уравнение (4.22) показывает, что зависимость момента инерции от конфигурации кинематической схемы приводит к существенному усложнению математической модели электропривода, появлению нелинейных слагаемых и неопределенных коэффициентов. Неопределенность коэффициентов в некоторых случаях можно устранить нахождением уравнений аналитических зависимостей всех связей между подсистемами проводов, но в большинстве случаев это оказывается затруднительно и поэтому рассматривают модель автономного электропривода с переменными динамическими параметрами и возмущениями, приведенными к валу исполнительных двигателей [113]. При такой постановке задачи момент инерции рассматривается как функция времени и, следовательно, уравнение для кинетической энергии автономного привода примет вид:
$$
W_{ki}=\frac{J_i(t)\omega_i(t)^2}{2}.\qquad
(4.23)$$
Подставляя (4.23) в уравнение Лагранжа (4.20) получим:

$$
J_i(t)\frac{d\omega_i(t)}{dt}+\omega_i(t)\frac{dJ_i(t)}{dt}=M_d-M_c,
$$
где $M_d$ — момент двигателя. $M_c$ — момент сопротивления. Таким образом механическая подсистема $i$-го электропривода примет описывается следующим образом:
$$
\begin{split}
&\dot \varphi_i(t)=\omega_i;\\
&\dot \omega_i(t)=\frac{1}{J_i(t)}(M_d-M_c-\frac{dJ_i(t)}{dt}\omega_i),
\end{split}\qquad
(4.24)$$где $\varphi_i$ — угол поворота, $\omega_i$ — скорость вращения вала электропривода.

Перейдем к синтезу синергетической системы управления электроприводами ангулярных роботов на основе формирования в ней свойств искусственной самоорганизации [61, 59]. Учитывая (4.24) запишем математическую модель автономного электропривода робота при $\text{Ф}=const$ в виде:
$$
\left\{
\begin{aligned}
&\dot \omega(t)=\frac{ki_{\textit{я}}-M_c-\dot J(t)\omega}{J(t)};\\
&\dot i_{\textit{я}}(t)=\frac{u_{\textit{я}}-k\omega-r_{\textit{я}}i_{\textit{я}}}{L_{\textit{я}}}.
\end{aligned}
\right.\qquad
(5.25)$$
где $k=c\,\text{Ф}_{\textit{ном}}$.

Параметрическая неопределенность объекта (4.25) возникает из-за изменения во времени приведенного момента инерции $J(t)$ и его производной $\dot J(t)$. Действие же внешней среды определяется моментом сопротивления $M_c$. В зависимости от характера изменения во времени этих моментов и их текущих оценок $\hat J(t)$ и $\hat M_c$ можно построить разные модели синтеза системы. Затем на основе этих моделей следует методом АКАР [61, 59] построить соответствующие законы адаптивного управления $u_{\textit{я}}(\omega,i_{\textit{я}},\hat J,\hat M_c)$, которые обеспечивают инвариантность замкнутой системы к указанным изменениям моментов при решении задачи стабилизации скорости электропривода. В [113] рассмотрены два варианта изменения приведенного момента инерции $J(t)$: в виде линейной функции времени $J_1=J_0+at$ и в виде гармонической функции $J_2=b\sin w_0t$. При этом в [113] момент сопротивления не учитывался, т.е. полагалось $M_c=0$. В зависимости от выбранного варианта изменения моментов $J(t)$ и $M_c$ можно на основе метода АКАР синтезировать разные синергетические динамические и адаптивные регуляторы. Рассмотрим эти варианты синтеза регуляторов скорости вращения электроприводов роботов.

4.2.2. Синтез динамического регулятора при линейном изменении момента инерции

Будем полагать, что момент инерции описывается функцией времени
$$
J(t)=J_0+at+b\sin w_0t\qquad
(4.26)$$которая объединяет частные виды функций, рассмотренных в [113]. Предположим сначала, что частота гармонического воздействия $w_0$ ограничена, что позволяет представить $J(t)$ в линейном приближении
$$
J(t)\cong J_0+at+bw_0t.\qquad
(4.27)$$Тогда динамическая модель момента сопротивления $M_c=M_0=const$ и производной момента инерции $\dot J(t)\cong a+bw_0=const$ можно, согласно методу АКАР, представить в виде двух интеграторов:
$$
\dot\nu_1(t)=\beta_1(\omega-\omega^*);\dot\nu_2(t)=\beta_2(\omega-\omega^*),\qquad
(4.28)$$где $\nu_1=\hat M_0$ — оценка момента сопротивления, $\nu_2=\hat a+\hat b\hat w_0$ — оценка приведенного момента инерции. Из (4.28) следует, что в момент $\omega=\omega^*$, т.е. достижения заданной скорости вращения электропривода, указанные возмущения “подавляются”. Если допустить, что “одавление” возмущений происходит одновременно, т.е. при $\beta_1=\beta_2=\beta$, то модель возмущения можно представить одним интегратором:
$$
\dot z_1(t)=\beta(\omega-\omega^*).\qquad
(4.29)$$где $z_1 $ — оценка неизмеряемых постоянных величин $\{\hat M_0,\hat a+\hat b\hat w_0\}$.

Для выдерживания соотношения (4.27) следует обеспечить скорость изменения переменной $z_1$ (4.29), существенно превосходящую динамику возмущения (4.27). Для этого необходимо выполнить следующее условие:
$$
2\pi\beta^2>>w_0.\qquad
(4.30)$$Тогда, полагая, что выполняется условие (4.30), сформируем с учетом (4.29) простую модель расширенной системы синтеза
$$
\left\{
\begin{aligned}
&\dot \omega(t)=\frac{ki_{\textit{я}}-z_1}{J_0};\\
&\dot i_{\textit{я}}(t)=\frac{u_{\textit{я}}-k\omega-r_{\textit{я}}i_{\textit{я}}}{L_{\textit{я}}};\\
&\dot z_1(t)=(\omega-\omega^*)\beta.
\end{aligned}
\right.\qquad
(4.31)$$Заметим, что в отличие от (4.25) в знаменатель правой части первого уравнения системы (4.31) вместо $J(t)$ введено номинальное значение $J_0$. Дело в том, что функция $J(t)$ в (4.25) отражает лишь инерционные свойства электропривода, т.е. фактически масштабирует переходные процессы и не влияет на установившейся режим движения. Таким образом, модель (4.31) используется для синтеза закона управления $u_{1\textit{я}}(\omega,i_{\textit{я}},z_1)$ т.е. динамического регулятора, подавляющего неизмеряемые возмущения $J(t)$ (4.26) и $M_0$, действующие на объект (4.25). В соответствии с методом АКАР введем макропеременную вида
$$
\psi_1=ki_{\textit{я}}-z_1+\alpha\omega+\gamma z_1.\qquad
(4.32)$$

Подставляя $\psi_1$ (4.32) в функциональное уравнение
$$
T_1\dot\psi_1(t)+\psi_1=0,\qquad
(4.33)$$и решая его совместно с (4.31) и (4.33), находим закон управления
$$
u_{1\textit{я}}=k+r_{\textit{я}}i_{\textit{я}}+\frac{\beta L_{\textit{я}}}{k}(\omega-\omega^*)(1-\gamma)%+\\
+\frac{L_{\textit{я}}(z_1-\alpha)}{kJ_0}(ki_{\textit{я}}-z_1)-\frac{L_{\textit{я}}}{kT_1}\psi_1,\qquad
(4.34)$$где $z_1=\beta\int(\omega-\omega^*)dt$.

Закон управления $u_{1\textit{я}}$ (4.34) переводит изображающую точку на многообразие $\psi_1=0$ (4.32), движение вдоль которого описывается дифференциальными уравнениями
$$
J_0\dot \omega_{\psi_1}(t)=-\alpha \omega_{\psi_1}-\gamma z_{1\psi_1};
\dot z_{1\psi_1}(t)=\beta(\omega_{\psi_1}-\omega_{\psi_1}^*).\qquad
(4.35)$$
объединяя которые в одно, имеем
$$
J_0\ddot \omega_{\psi_1}(t)+\alpha\dot \omega_{\psi_1}(t)+\gamma\beta(\omega_{\psi_1}-\omega_{\psi_1}^*)=0.\qquad
(4.36)$$
Уравнение (4.36) описывает движение координаты $\omega_{\psi_1}$ вдоль $\psi_1=0$ (4.32). При выборе коэффициентов $\alpha>0,\gamma\beta>0$ уравнение (4.36) и, следовательно, замкнутая система (4.25), (4.34) будут асимптотически устойчивыми относительно состояния $\omega=\omega^*$. Для выбора коэффициентов $\alpha,\beta,\gamma$ можно использовать декремент затухания $\xi$ системы (4.36), т.е. $\alpha=2\xi\sqrt{\gamma\beta J_0}$.

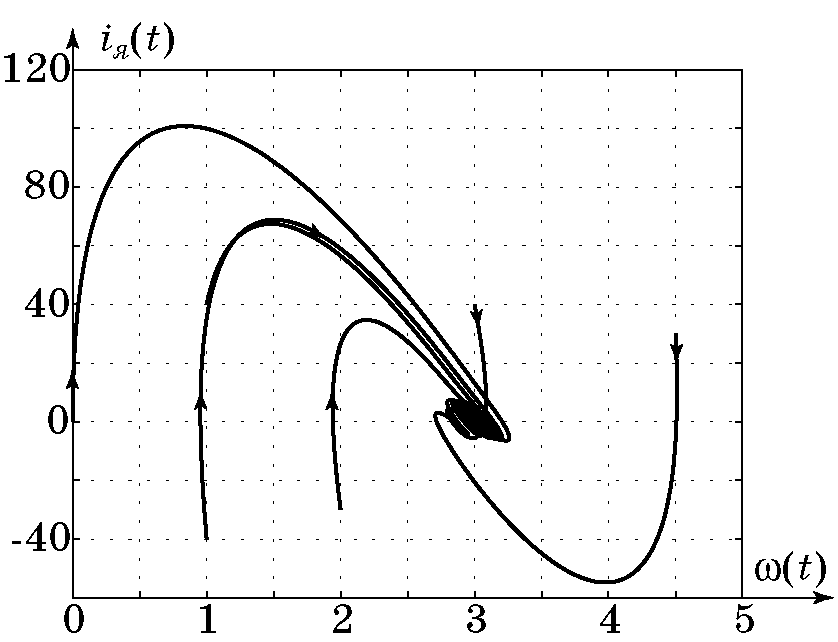
Смоделируем сначала замкнутую систему (4.25), (4.34) при условии, что момент инерции $J(t)$ изменяется по линейному закону (4.27) во времени. На рис. 4.3 и рис. 4.4 приведены соответствующие графики изменения координат, управления и макропеременной. Эти результаты моделирования показывают, что синтезированный динамический регулятор (4.34) успешно приспосабливает систему к параметрическому $\dot J(t)$ и внешнему $M_c$ возмущениям.

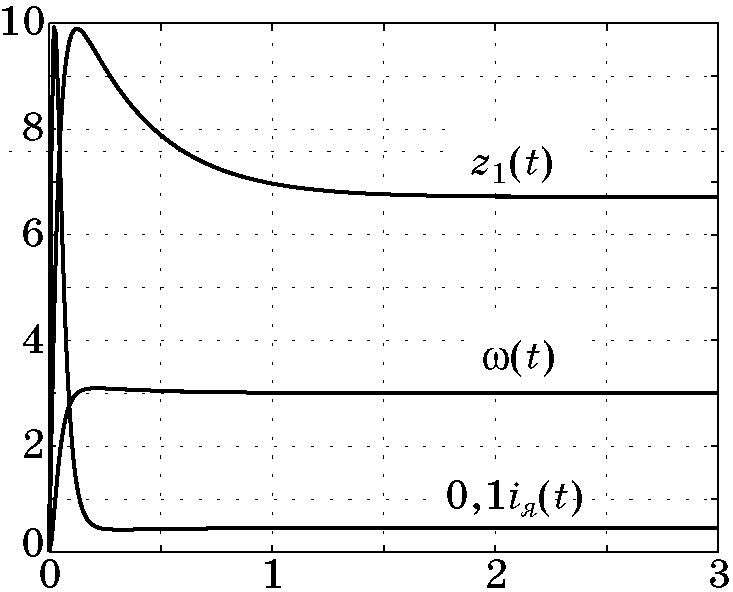
Рис. 4.3. Изменение координат

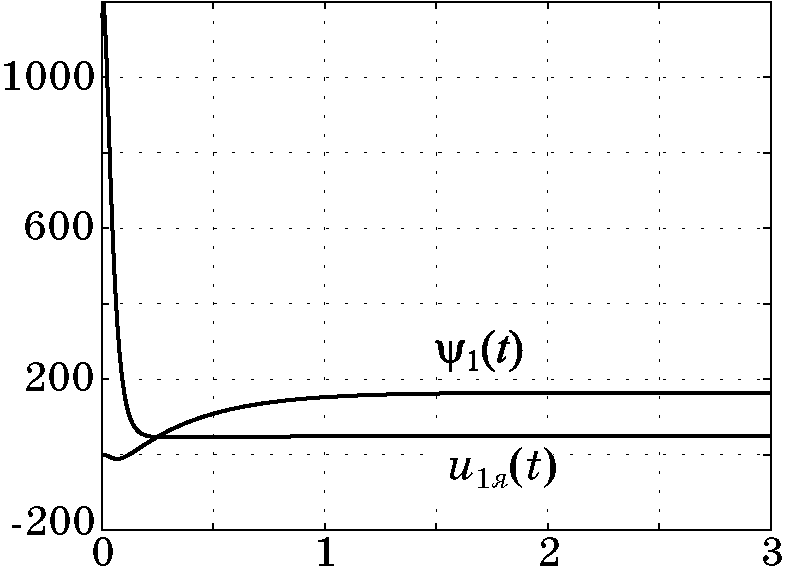
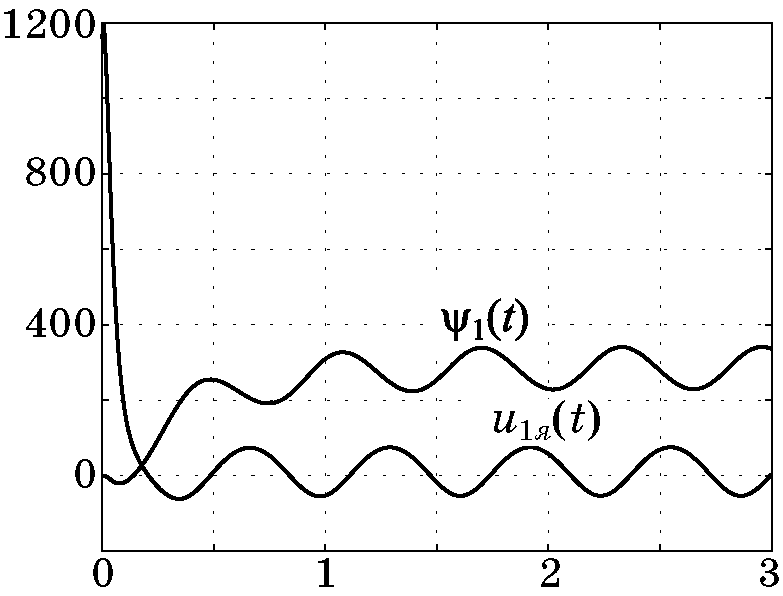
Рис. 4.4. Изменение управления и макропеременной

Предположим теперь, что параметрическое возмущение $\dot J(t)$ имеет гармонический характер. На рис. 4.5, рис. 4.6, рис. 4.7, рис. 4.8 приведены графики моделирования замкнутой системы (4.25), (4.34) при следующих параметрах: $M_c=1$, $J_0=2$, $a=0,2$, $b=0,1$, $w_0=10$, $\omega^*=3$, $\xi=1$, $\beta=-25$, $\gamma=-50$, $\alpha=2$. На рис. 4.6 приведены графики изменения отклонения $\varepsilon=\omega(t)-\omega^*$ для разных значений $\beta^2=\lambda^2\dfrac{w_0}{2\pi}$ при $\lambda=\{30,70,100\}$, т.е. для разной силы неравенства (4.30).

 

Рис. 4.5. Фaзовый портрет системы

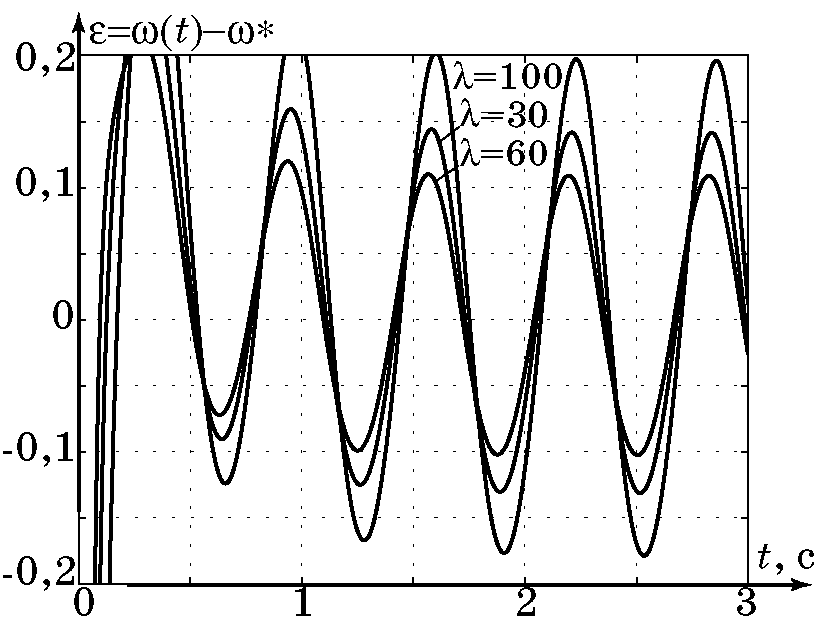
Рис. 4.6. Изменение отклонения

Рис. 4.7. Изменение координат

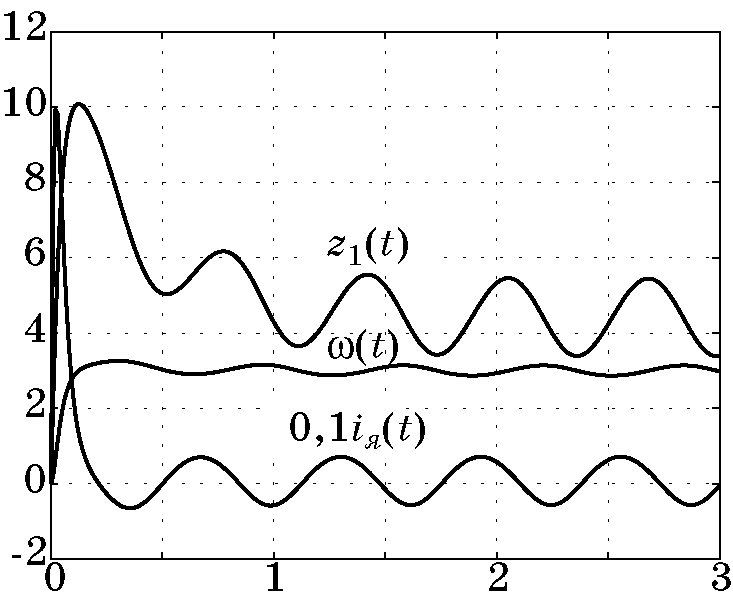
Рис. 4.8. Изменение управления и макропеременной

В целом, результаты исследования замкнутой системы (4.25), (4.34) свидетельствуют о том, согласно [113], простой синергетический регулятор (4.34) обладает своего рода “интеллектом”, позволяющим ему успешно приспосабливаться к параметрическим и внешним возмущениям, действующим на систему.

4.2.3. Синтез динамического регулятора при линейно-гармоническом изменении момента инерции

Будем теперь полагать, что изменение момента инерции во времени описывается исходной функцией (4.26). Тогда динамическая модель момента сопротивления $M_c=M_0=const$ и производной момента инерции $\dot J(t)=a+bw_0\cos w_0t$ можно, согласно методу АКАР, представить в виде интегратора и колебательного звена:
$$
\left\{
\begin{aligned}
&\dot z_1(t)=(\omega-\omega^*)\beta;\\
&\dot z_2(t)=z_3+z_1;\\
&\dot z_3(t)=-w_0^2z_2.
\end{aligned}
\right.\qquad
(4.37)$$где $z_1$ — оценка постоянного возмущения, $z_2,z_3$ — оценка гармонического возмущения. Из (4.37) следует, что в момент $\omega=\omega^*$, т.е. достижения заданной скорости вращения электропривода, указанные возмущения подавляются. Тогда, учитывая структуру возмущения (4.26) и модель обекта (4.25), расширенная модель синтеза запишется в виде:
$$
\left\{
\begin{aligned}
&\dot \omega(t)=\frac{ki_{\textit{я}}-z_1-\omega z_3}{J_0};\\
&\dot i_{\textit{я}}(t)=\frac{u_{\textit{я}}-k\omega-r_{\textit{я}}i_{\textit{я}}}{L_{\textit{я}}};\\
&\dot z_1(t)=(\omega-\omega^*)\beta;\\
&\dot z_2(t)=z_3+z_1;\\
&\dot z_3(t)=-w_0^2z_2.
\end{aligned}
\right.\qquad
(4.38)$$Модель (4.38) используется для синтеза закона управления $u_{2\textit{я}}(\omega,i_{\textit{я}},z_1,z_2,z_3)$ т.е. динамического регулятора, подавляющего неизмеряемые возмущения $J(t)$ (4.26) и $M_0$, действующие на объект (4.25).

Для синтеза закона управления $u_{2\textit{я}}$, согласно методу АКАР, последовательно введем макропеременные
$$
\psi_1=ki_{\textit{я}}-z_1-\omega z_3-\varphi_1;\,\psi_2=(\omega-\omega^*)\beta-\varphi_2;\,\psi_3=z_1+\lambda z_2. \qquad
(4.39)$$

Тогда на основе функциональных уравнений
$$
T_i\psi_i(t)+\psi_i=0,\,i=1,2,3\qquad
(4.40)$$

и уравнений системы находится закон внешнего управления $u_{2\textit{я}}(\omega,i_{\textit{я}},z_1,z_2,z_3)$, который переводит изображающую точку системы вдоль многообразий $\psi_i=0$.

Для задания внутренних свойств объекта рассмотрим поведение расширенной системы на многобразии $\psi_3=0$:
$$
\ddot z_{2\psi_3}(t)+\lambda\dot z_{2\psi_3}(t)+w_0^2z_{2\psi_3}=0
$$
Декремент затухания последнего уравнеия равен $\xi=\frac{\lambda}{2w_0}$. При $\xi=1$, получаем:
$$
\lambda=2w_0.\qquad
(4.41)$$

Выполнив процедуру синергетического синтеза на основе уравнений (4.39),(4.40) и объекта (4.38), с учетом равенства (4.41) получим закон управления
$$
\begin{split}
&u_{2\textit{я}}=\frac{J_0L_{\textit{я}}(\omega-\omega^*)(1+2w_0(T_2+T_3))+L_{\textit{я}}(\omega z_3+z_1)(T_2+T_3)}{T_2T_3k}+\frac{\psi_1}{T_1k}+\\
&+\frac{2L_{\textit{я}}(\omega z_3+z_1)(J_0w_0+2z_1)+L_{\textit{я}}i_{\textit{я}}k(z_1+z_3)}{J_0k}-2Lw_0i_{\textit{я}}+k\omega+r_{\textit{я}}i_{\textit{я}}+\\
&+\frac{w_0L_{\textit{я}}\omega(2(z_1+z_3)-w_0z_2)}{k}-\frac{2J_0w_0^3L_{\textit{я}}T_2T_3((z_1+z_3)+z_2(T_2T_3)}{T_2T_3\beta k},
\end{split}\qquad
(4.42)$$

где $\psi_1=\dfrac{(T_2+T_3)(2w_0(z_1+z_3)+\beta(\omega-\omega^*))+z_1+2w_0z_2-2w_0^3z_2T_2T_3}{T_2T_3J_0}+\dfrac{2w_0(\omega-\omega^*)}{J_0}$.

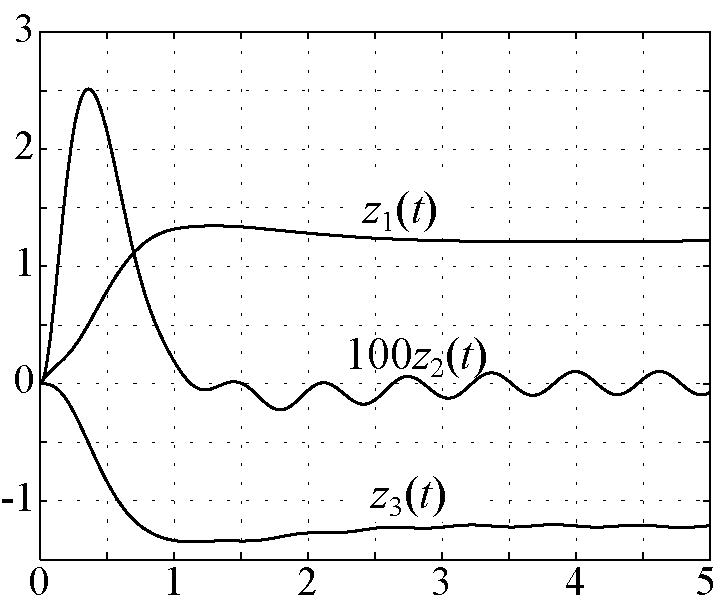
Рис. 4.9. Изменение переменных состояния расширенной подсистемы

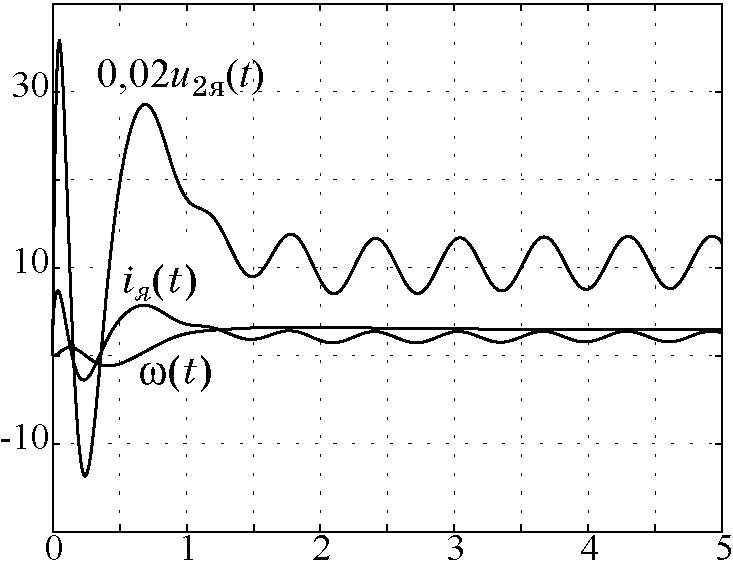
Рис. 4.10. Изменение координат и управления

На рис. 4.11 — рис. 4.12 приведены графики моделирования замкнутой системы (4.25),(4.37) с законом управления (4.42), при следующих параметрах модели
$$J_0=2,\;M_c=5,\;J_0=2,\;a=0.2,\;b=0.1,\;w_0=10,\;L_{\textit{я}}=0.1,\;k=1,r_{\textit{я}}=10$$

и регулятора
$$\omega^*=3,\;\beta=0.5,\;T_1=0.4,\;T_2=0.2,\;T_3=0.5.$$

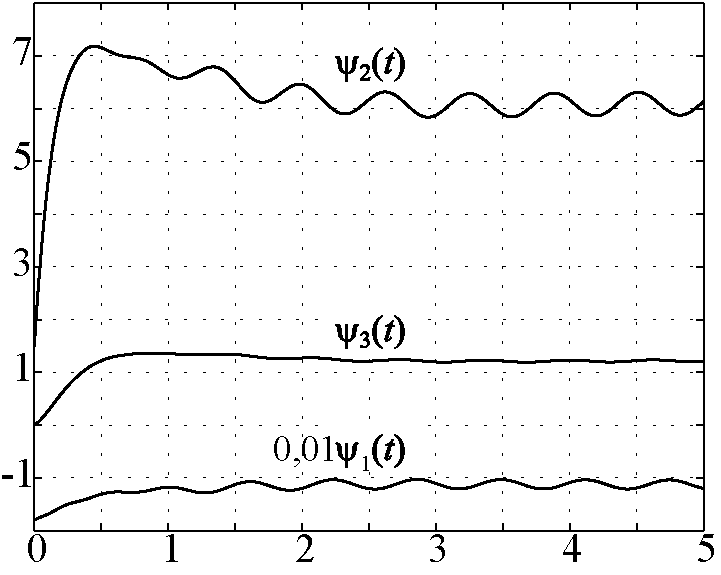
Рис. 4.11. Изменение макропеременных

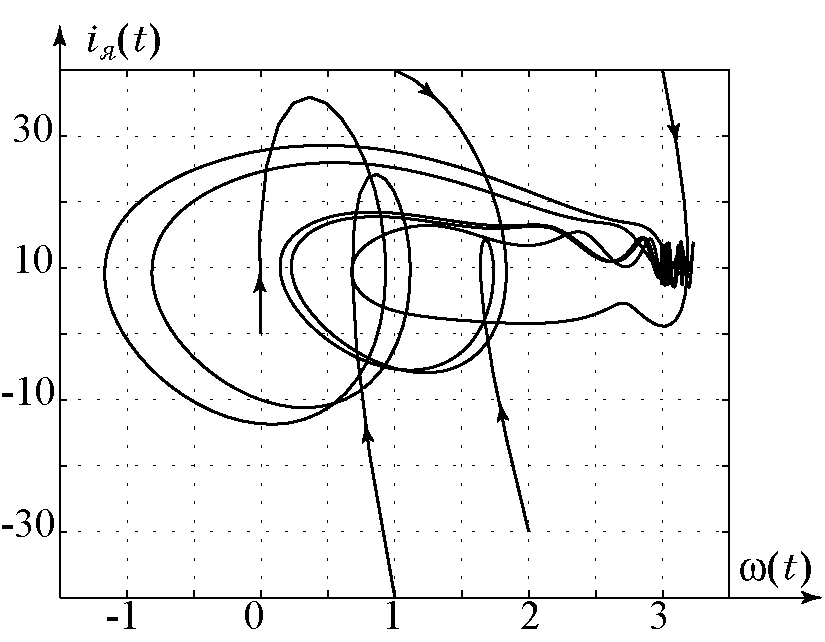
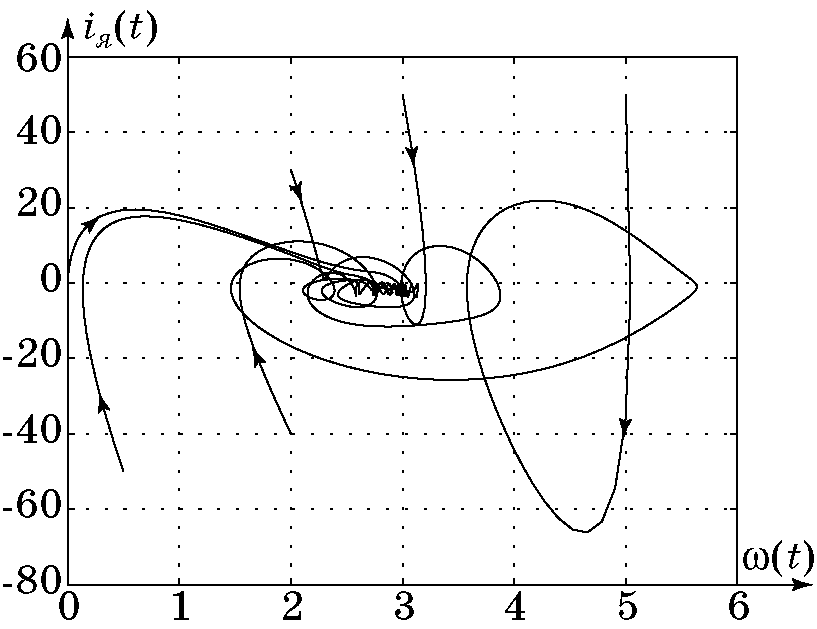
Рис. 4.12. Фазовый портрет системы

Синтезированный динамический регулятор (4.42) наглядно показывают эффективность применения синергетического подхода для решения задач подавления неизмеряемых параметрических и внешних возмущений.

4.2.4. Построение наблюдателя при гармоническом изменении момента инерции

Синтезируем теперь адаптивный синергетический регулятор с наблюдателями момента инерции $J(t)$, изменяющегося по гармоническому закону, и момента сопротивления, который предполагается постоянным.

Для построения этих наблюдателей сначала строятся модели указанных возмущений $J(t)$ и $M_c$, т.е.
$$
\dot\nu_1(t)=\nu_2,\,
\dot\nu_2(t)=-w_0^2\nu_1,\,
\dot J(t)=\nu_2,\,
\dot\nu_3(t)=0,\,
M_c=\nu_3.
$$

Далее записывается расширенная модель синтеза системы, в которой реальные возмущения заменяют их моделями
$$
\left\{
\begin{aligned}
&\dot \omega(t)=\frac{ki_{\textit{я}}-\nu_3-\nu_2\omega}{J_0};\\
&\dot i_{\textit{я}}(t)=\frac{u_{\textit{я}}-k\omega-r_{\textit{я}}i_{\textit{я}}}{L_{\textit{я}}};\\
&\dot\nu_1(t)=\nu_2;\\
&\dot\nu_2(t)=-w_0^2\nu_1;\\
&\dot\nu_3(t)=0.
\end{aligned}
\right.\qquad
(4.43)$$

Разумеется модель синтеза (4.43) по сравнению с моделью (4.37) более точно отражает возмущения $\dot J(t)$ и $M_c$, однако это очевидно приведет к более сложному регулятору, приспосабливающемуся к возмущениям.

Поскольку наблюдаемые в объекте (4.43) переменные входят только в уравнение для скорости, то достаточно рассмотреть построение наблюдателя для упрощенной системы:
$$
\left\{
\begin{aligned}
&\dot \omega(t)=\frac{ki_{\textit{я}}-\nu_3-\nu_2\omega}{J_0};\\
&\dot\nu_1(t)=\nu_2;\\
&\dot\nu_2(t)=-w_0^2\nu_1;\\
&\dot\nu_3(t)=0.
\end{aligned}
\right.\qquad
(4.44)
Согласно [61, 59] для построения наблюдателя переменных $\nu_1,\nu_2$ и $\nu_3$ сформируем вектор макропеременных:
$$
\Psi=
\begin{bmatrix}
&\nu_1-\hat\nu_1 \\
&\nu_2-\hat\nu_2 \\
&\nu_3-\hat\nu_3
\end{bmatrix},
$$

изменение которого во времени должно подчиняться дифференциальным уравнениям
$$
\dot\Psi(t)-\BS{L}\Psi=0\qquad
(4.45)$$где $\BS{L}$ — матрица, определяющая устойчивость дифференциальных уравнений.
Запишем дифференциальные уравнения (4.45) в развернутом виде:
$$
\begin{split}
&\nu_2-\dot{\hat\nu}_1(t)-l_{11}(\nu_1-\hat\nu_1)-l_{12}(\nu_2-\hat\nu_2)-l_{13}(\nu_3-\hat\nu_3)=0; \\
&-w_0^2\nu_1-\dot{\hat\nu}_2(t)-l_{21}(\nu_1-\hat\nu_1)-l_{22}(\nu_2-\hat\nu_2)-l_{23}(\nu_3-\hat\nu_3)=0; \\
&-\dot{\hat\nu}_3(t)-l_{31}(\nu_1-\hat\nu_1)-l_{32}(\nu_2-\hat\nu_2)-l_{33}(\nu_3-\hat\nu_3)=0.
\end{split}
$$

где $l_{ij}$ — элементы матрицы $\BS{L}$.
Выполнив замену переменной $\nu_3=ki_{\textit{я}}-\nu_2\omega-\dot \omega(t) J_0$, в соответствии с моделью (4.44), уравнения наблюдателя запишутся в виде:
$$
\begin{split}
&\nu_2-\dot{\hat\nu}_1(t)-l_{11}(\nu_1-\hat\nu_1)-l_{12}(\nu_2-\hat\nu_2)-l_{13}(ki_{\textit{я}}-\nu_2\omega-\dot \omega(t)J_0-\hat\nu_3)=0; \\
&{-}w_0^2\nu_1{-}\dot{\hat\nu}_2(t){-}l_{21}(\nu_1{-}\hat\nu_1){-}l_{22}(\nu_2{-}\hat\nu_2){-}l_{23}(ki_{\textit{я}}{-}\nu_2\omega{-}\dot \omega(t)J_0{-}\hat\nu_3){=}0; \\
&-\dot{\hat\nu}_3(t)-l_{31}(\nu_1-\hat\nu_1)-l_{32}(\nu_2-\hat\nu_2)-l_{33}(ki_{\textit{я}}-\nu_2\omega-\dot \omega(t)J_0-\hat\nu_3)=0.
\end{split}\qquad
(4.46)$$

Поскольку ненаблюдаемые координаты должны отсутствовать в уравнениях наблюдателя, то выберем значения элементов матрицы $\BS{L}$ следующим образом:
$$
l_{11}=0,\, l_{12}=1+l_{13}\omega,\, l_{21}=-w_0^2,\, l_{22}=l_{23}\omega,\, l_{31}=0,\, l_{32}=l_{33}\omega.
$$

Оставшиеся три элемента $l_{13},l_{23}$ и $l_{33}$ найдем задав собственные значения матрицы $\BS{L}$. Характеристический полином матрицы $\BS{L}$ равен:
$$
\begin{split}
\det(p\BS{E}-\BS{L})=&
\begin{bmatrix}
& p & -1-l_{13}\omega & -l_{13} \\
& w_0^2 & p-l_{23}\omega & -l_{23} \\
& 0 & -l_{33}\omega & p-l_{33}
\end{bmatrix}=\\
=&p^3-(l_{33}+l_{23}\omega)p^2+(w_0^2l_{13}\omega+w_0^2)p+w_0l_{33}.
\end{split}
$$

Выберем желаемый характеристический полином так, чтобы в уравнениях наблюдателя не появилось деления на переменную $\omega$. Данный полином можно сформировать в виде:
$$
\begin{split}
\Lambda=&(p^2+w_0^2\omega^2\lambda_1p+w_0^2)(p+\omega^2\lambda_2)=\\
=&p^3-(w_0^2\omega^2\lambda_1+\omega^2\lambda_2 )p^2+(w_0^2+w_0^2\omega^4\lambda_1\lambda_2)p-w_0^2\omega^2\lambda_2,
\end{split}
$$

где $\lambda_1,\lambda_2$ — некоторые положительные числа, задающие динамику наблюдателя.

Последнее уравнение имеет следующие решения:
$$
p_{1,2}=-\frac{1}{2}\omega^2\lambda_1w_0^2\pm\frac{w_0}{2}\sqrt{\omega^4w_0^2\lambda_1^2-4},\quad p_3=-\omega^2\lambda_2,
$$

которые имеют отрицательную вещественную часть при любых положительных значениях $\lambda_1$ и $\lambda_2$.

Сопоставляя желаемый полином с характеристическим полиномом матрицы $\BS{L}$ найдем элементы $l_{13},l_{23}$ и $l_{33}$:
$$
l_{13}=\omega^3\lambda_1\lambda_2,l_{23}=-\omega w_0^2\lambda_1,l_{33}=-\omega^2\lambda_2.
$$
В соответствии с найденными элементами матрицы $\BS{L}$ перепишем уравнения наблюдателя (4.46):

\begin{split}
&-\dot{\hat\nu}_1(t)+(1-\omega^4\lambda_1\lambda_2)\hat\nu_2-\omega^3\lambda_1\lambda_2(ki_{\textit{я}}-\dot \omega(t)J_0-\hat\nu_3)=0; \\
&-\dot{\hat\nu}_2(t)-w_0^2\hat\nu_1-w_0^2\omega^2\lambda_1\hat\nu_2+\omega w_0^2\lambda_1(ki_{\textit{я}}-\dot \omega(t)J_0-\hat\nu_3)=0; \\
&-\dot{\hat\nu}_3(t)-\omega^3\lambda_2\hat\nu_2+\omega^2\lambda_2(ki_{\textit{я}}-\dot \omega(t)J_0-\hat\nu_3)=0.
\end{split}\qquad
(4.47)$$

Тогда в соответствии с синергетическим методом [61, 59]} после замены переменных $z_1=\hat\nu_1-\dfrac{J_0\lambda_1\lambda_2\omega^4}{4}$, $z_2=\hat\nu_2+\dfrac{J_0w_0^2\lambda_1\omega^2}{2}$, $z_3=\hat\nu_3+\dfrac{J_0\lambda_2\omega^3}{3}$ получим уравнения наблюдателя для координат $\nu_1,\nu_2$ и $\nu_3$:
$$
\left\{
\begin{aligned}
&\dot z_1(t)=(1{-}\omega^4\lambda_1\lambda_2)\left(z_2{-}\frac{J_0w_0^2\lambda_1\omega^2}{2}\right){-}\omega^3\lambda_1\lambda_2\left(ki_{\textit{я}}{-}z_3{+}\frac{J_0\lambda_2\omega^3}{3}\right){=}0; \\
&\dot z_2(t)=-w_0^2\left(z_1+\frac{J_0\lambda_1\lambda_2\omega^4}{4}\right)-w_0^2\omega^2\lambda_1\left(z_2-\frac{J_0w_0^2\lambda_1\omega^2}{2}\right)+\\
&+\omega w_0^2\lambda_1\left(ki_{\textit{я}}-z_3+\frac{J_0\lambda_2\omega^3}{3}\right)=0; \\
&\dot z_3(t)=-\omega^3\lambda_2\left(z_2-\frac{J_0w_0^2\lambda_1\omega^2}{2}\right)+\omega^2\lambda_2\left(ki_{\textit{я}}-z_3+\frac{J_0\lambda_2\omega^3}{3}\right)=0; \\
&\hat\nu_1=z_1+\frac{J_0\lambda_1\lambda_2\omega^4}{4}; \\
&\hat\nu_2=z_2-\frac{J_0w_0^2\lambda_1\omega^2}{2}; \\
&\hat\nu_3=z_3-\frac{J_0\lambda_2\omega^3}{3};
\end{aligned}
\right.\qquad
(4.48)$$

Синергетический закон управления для расширенной математической модели (4.43) был получен в виде:
$$
\begin{split}
&u_{\textit{я}}(x)=-\frac{L_{\textit{я}}\nu_2(i_{\textit{я}}-\nu_3-\nu_2\omega)}{kJ_0}+\frac{L_{\textit{я}}(\nu_3-ki_{\textit{я}}+\nu_2\omega)}{T_2k}+\\
&+\frac{\hat{\dot\nu}_2(t)\omega L_{\textit{я}}T_1T_2-i_{\textit{я}}L_{\textit{я}}kT_2+\nu_3L_{\textit{я}}T_2+L_{\textit{я}}\nu_2\omega T_2-J_0L_{\textit{я}}(\omega-\omega^*)}{kT_1T_2},
\end{split}
(4.49)$$
где
$$
\begin{split}
&\hat{\dot\nu}_2(t)=\dot z_2(t)-J_0w_0^2\lambda_1\omega\dot \omega(t)=-w_0^2\lambda_1\omega\left(ki_{\textit{я}}-M_c-\left(z_2-\frac{J_0w_0^2\lambda_1\omega^2}{2}\right)\omega\right)-\\
&{-}\left(w_0^2\left(z_1{+}\frac{J_0\lambda_1\lambda_2\omega^4}{4}\right){+}w_0^2\omega^2\lambda_1\left(z_2{-}\frac{J_0w_0^2\lambda_1\omega^2}{2}\right){-}\omega w_0^2\lambda_1\left(ki_{\textit{я}}{-}z_3{+}\frac{J_0\lambda_2\omega^3}{3}\right)\right).
\end{split}
$$

Моделирование электропривода с математической моделью
$$
\left\{
\begin{aligned}
&\dot \omega(t)=\frac{ki_{\textit{я}}-M_c-\omega aw_0\cos w_0t}{J_0+a\sin w_0t};\\
&\dot i_{\textit{я}}(t)=\frac{u_{\textit{я}}-k\omega-r_{\textit{я}}i_{\textit{я}}}{L_{\textit{я}}},
\end{aligned}
\right.
$$

законом управления (4.49) и наблюдателем возмущения (4.48) приведены на рис. 4.13, рис. 4.14, рис. 4.15, рис. 4.16.
Моделирование проводилось при следующих параметрах

$\lambda_1=1$, $\lambda_2=0,5$, $\lambda_3=1,5$, $T=0,1$, $J_0=1$, $a=0,1$, $M_c=0,8$, $\omega^*=3$, $w_0=3$.

Рис. 4.13. Фазовый портрет системы

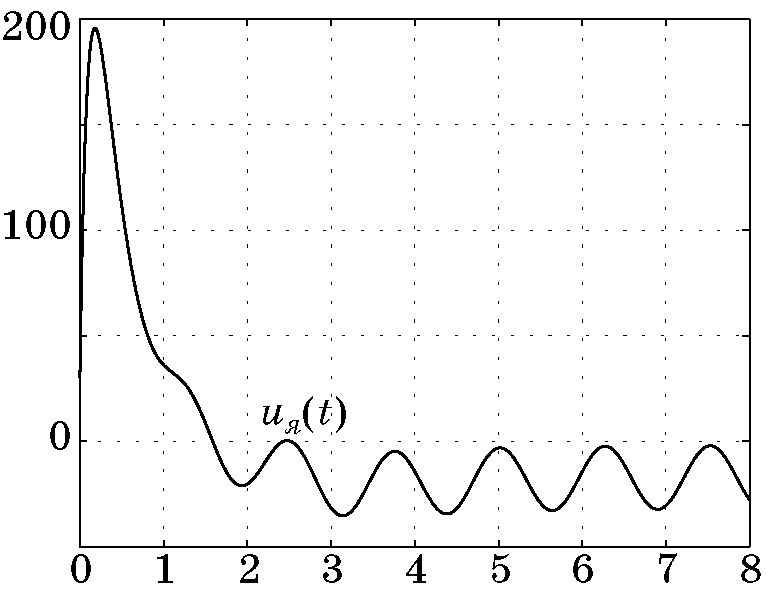
Рис. 4.14. Управляющее воздействие

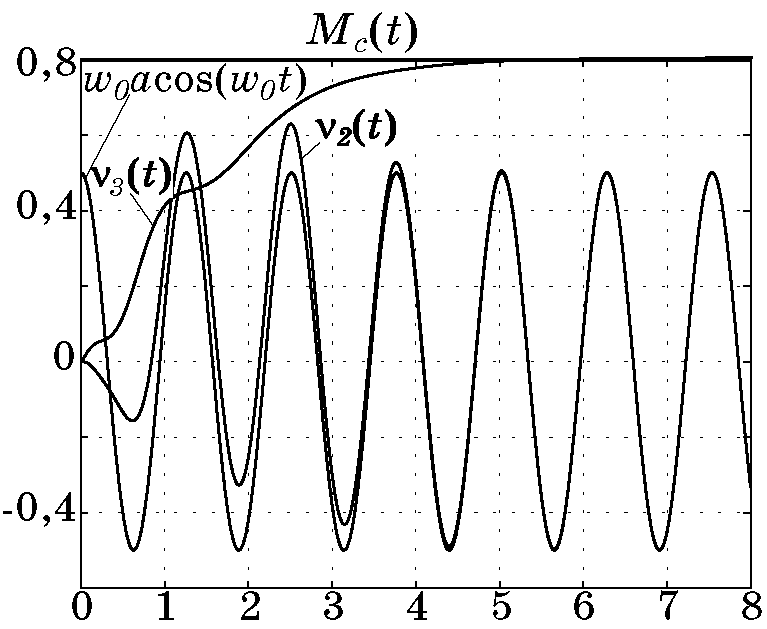
Рис. 4.15. Изменения возмущений и их оценок


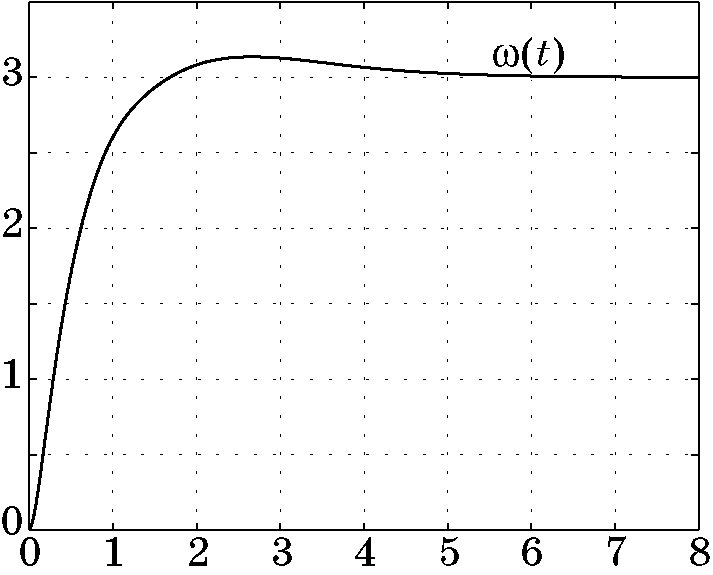
Рис. 4.16. Изменение выходной координаты

Результаты моделирования показывают, что синтезированный методом АКАР адаптивный регулятор отслеживает изменение неизмеряемых возмущений и обеспечивает стабилизацию выходной переменной системы. Этот регулятор можно, согласно терминологии [113], также отнести к так называемым “интеллектуальным регуляторам”, которые успешно приспосабливаются к параметрическим и внешним возмущениям.