Модуль 4. Аналитическое конструирование динамических регуляторов с наблюдателями состояния

4.1. Метод синтеза наблюдателей

4.1.1. Постановка задачи

$$
\begin{split}
\dot{\mathbf y} &=\mathbf{g(y,v,u)};\\
\dot{\mathbf v} &=\mathbf{h(y,v,u)},\\
\end{split}\qquad
(5.1)$$

где n-вектор $\mathbf y$ и m-вектор $\mathbf v$ — компоненты вектора состояния; $\mathbf u$ — вектор управления; $\mathbf g(\cdot)$ и $\mathbf h(\cdot)$ — непрерывные нелинейные функции. Вектор $\mathbf y$ предполагается наблюдаемым, а вектор $\mathbf v$ — ненаблюдаемым.

Задача заключается в построении асимптотической оценки вектора $\mathbf v$ по наблюдаемым значениям вектора $\mathbf y$ и известному, как функции времени, вектору $\mathbf u$. К такой постановке приводят рассматриваемые ниже задачи синтеза нелинейных систем при неполной информации о векторе состояния объекта, задачи построения нелинейных систем, инвариантных к воздействиям заданной формы, задачи адаптивного управления нелинейными объектами и другие.

4.1.2. Уравнения наблюдателя

Введем в рассмотрение m-вектор $\boldsymbol\psi(t)$, определяемый формулой
$$
\boldsymbol\psi(t)=\boldsymbol\phi(\mathbf{y,v}) -\hat{\boldsymbol\phi}(t),\qquad
(4.2)$$где функции $\boldsymbol\phi$ и $\hat{\boldsymbol\phi}(t)$ удовлетворяют следующим условиям:

1. $\boldsymbol\phi(\mathbf{y,v})$ и $\hat{\boldsymbol\phi}(t)$ непрерывны и дифференцируемы по своим аргументам;
2. Решение уравнения
   
   $$
   \boldsymbol\phi(\mathbf{y,v})-\hat{\boldsymbol\phi}=0\qquad
   (4.3)$$

относительно $\mathbf v$ существует и является единственным для всех $\mathbf y\in \mathcal{R}^n$.

Рассматривая вектор $\boldsymbol\psi$ как функцию времени, потребуем, чтобы он удовлетворял однородному дифференциальному уравнению
$$
\dot{\boldsymbol\psi}(t)=\mathbf{L(y)}\boldsymbol\psi,\qquad
(4.4)$$где $m\times m$ матрица $\mathbf{L(y)}$ такова, что тривиальное решение $\boldsymbol\psi=0$ асимптотически устойчиво в целом. В простейшем случае $\mathbf{L(y)}$ — числовая устойчивая матрица.

С учетом (4.2) и (4.1), уравнение (4.4) принимает вид
$$
\frac{\partial\boldsymbol\phi}{\partial \mathbf y}\mathbf{g(y,v,u)} +\frac{\partial\boldsymbol\phi}{\partial \mathbf v}\mathbf{h(y,v,u)} -\dot{\hat{\boldsymbol\phi}}=\mathbf{L(y)}\boldsymbol\phi(\mathbf{y,v})-\mathbf{L(y)}\hat{\boldsymbol\phi}.\qquad
(4.5)$$Предположим, что для заданных функций $\mathbf{g(y,v,u)}$ и $\mathbf{h(y,v,u)}$ найдутся такой вектор $\boldsymbol \gamma(\mathbf{y,u})$ и матрица $\boldsymbol\Gamma(\mathbf y)$, не зависящие от $\mathbf v$, что оказывается выполненным равенство
$$
\frac{\partial\boldsymbol\phi}{\partial \mathbf y}\mathbf{g(y,v,u)} +\frac{\partial\boldsymbol\phi}{\partial \mathbf v}\mathbf{h(y,v,u)} -\mathbf{L(y)\boldsymbol\phi(y,v)}=\boldsymbol\Gamma(\mathbf y)\mathbf{g(y,v,u)} +\boldsymbol \gamma(\mathbf{y,u}).\qquad
(4.6)$$Тогда уравнение (4.5) с учетом первого уравнения системы (4.1) примет вид
$$
\boldsymbol\Gamma(\mathbf y)\dot{\mathbf y} -\dot{\hat{\boldsymbol\phi}} +\boldsymbol \gamma(\mathbf{y,u}) +\mathbf{L(y)}\hat{\boldsymbol\phi}=0
$$

или
$$
\dot{\mathbf z}=\mathbf{L(y)z}-\mathbf{L(y)}\int\limits_0^{\mathbf y}\boldsymbol\Gamma(\mathbf y)d\mathbf y -\boldsymbol \gamma(\mathbf{y,u}),\qquad
(4.7)$$где
$$
\mathbf z=\int\limits_0^{\mathbf y}\boldsymbol\Gamma(\mathbf y)d\mathbf y -\hat{\boldsymbol\phi}.\qquad
(4.8)$$

При этом, согласно (4.2), (4.8), вектор
$$
\boldsymbol\psi=\boldsymbol\phi(\mathbf{y,v}) -\int\limits_0^{\mathbf y}\boldsymbol\Gamma(\mathbf y)d\mathbf y +\mathbf z.\qquad
(4.9)$$

Поскольку решение $\boldsymbol\psi=0$ уравнения (4.4) асимптотически устойчиво в целом, асимптотическая оценка $\hat{\mathbf v}$ ненаблюдаемого вектора $\mathbf v$ может быть найдена из уравнения
$$
\boldsymbol\phi(\mathbf{y,\hat v})=\int\limits_0^{\mathbf y}\boldsymbol\Gamma(\mathbf y)d\mathbf y -\mathbf z,\qquad
(4.10)$$

которое, согласно условию (4.3), имеет единственное решение относительно $\hat{\mathbf v}$ для всех $\mathbf{ y}\in\mathcal{R}^n$.

Уравнения (4.7) и (4.10) представляют собой уравнения асимптотического наблюдателя для ненаблюдаемого вектора $\mathbf v$ системы (4.1). При этом из (4.4) следует, что компоненты вектора $\boldsymbol\psi$, определяемого (4.9), представляют собой инвариантные многообразия в пространстве состояний системы (4.1), (4.7).

Задача синтеза наблюдателя сводится, таким образом, к нахождению функций $\boldsymbol\phi(\mathbf{y,v})$, $\mathbf{L(y)}$, $\boldsymbol\Gamma(\mathbf y)$ и $\boldsymbol\gamma(\mathbf y)$, удовлетворяющих уравнению (4.6). При этом функция $\boldsymbol\phi(\mathbf{y,v})$ должна отвечать указанным выше требованиям 1) и 2), а матрица $\mathbf{L(y)}$ — обеспечивать асимптотическую устойчивость системы (4.4).

4.1.3. Критерий наблюдаемости

Рассмотрим частный случай системы (4.1), когда векторы $\mathbf g$ и $\mathbf h$ являются линейными функциями вектора $\mathbf v$:
$$
\begin{split}
\mathbf{g(y,v,u)} &=\mathbf{g_0(y,u) +G_1(y)v};\\
\mathbf{h(y,v,u)} &=\mathbf{h_0(y,u) +H_1(y)v}.
\end{split}\qquad
(4.11)$$

Тогда можно положить
$$
\boldsymbol\phi(\mathbf{y,v})=\mathbf{Fv},\qquad
(4.12)$$

где $\mathbf F$ — числовая, устойчивая матрица. Подстановка (4.11), (4.12) в (4.6) приводит к следующей системе уравнений для $\boldsymbol\Gamma(\mathbf y)$, $\mathbf{L(y)}$, $\mathbf F$ и $\boldsymbol\gamma(\mathbf{y,u})$:
$$
\mathbf H_1^{\mathrm T}(\mathbf y) -\mathbf G_1^{\mathrm T}(\mathbf y)\big(\mathbf F^{-1}\boldsymbol\Gamma(\mathbf y)\big)^{\mathrm T}=\big(\mathbf F^{-1}\mathbf{LF}\big)^{\mathrm T}.\qquad
(4.13)$$

Положим $\mathbf{L(y)=L}$ — числовой матрице и запишем первое уравнение системы (4.13) в виде:
$$
\mathbf H_1^{\mathrm T}(\mathbf y) -\mathbf G_1^{\mathrm T}(\mathbf y)\big(\mathbf F^{-1}\boldsymbol\Gamma(\mathbf y)\big)^{\mathrm T}=\big(\mathbf F^{-1}\mathbf{LF}\big)^{\mathrm T}.\qquad
(4.14)$$

Отсюда видно, что собственные значения матрицы $\mathbf L$, определяющие динамику наблюдателя, могут быть назначены произвольно, если
$$
\mathrm{rang}\big|\mathbf G_1^{\mathrm T}(\mathbf y)\vdots \mathbf H_1^{\mathrm T}(\mathbf y)\mathbf G_1^{\mathrm T}(\mathbf y)\vdots\, \dots\,\vdots\big(\mathbf H_1^{\mathrm T}(\mathbf y)\big)^{m-1}\mathbf G_1^{\mathrm T}(\mathbf y)\big|=m; \quad \forall\mathbf y\in\mathcal{R}^n.\qquad
(4.15)$$

При этом в качестве $\mathbf F$ может быть выбрана любая неособая матрица. Положим $\mathbf F$ равной единичной матрице $\mathbf I$. Тогда (4.14) запишется в виде
$$
\mathbf H_1^{\mathrm T}(\mathbf y) -\mathbf G_1^{\mathrm T}(\mathbf y)\boldsymbol\Gamma^{\mathrm T}(\mathbf y)=\mathbf L^{\mathrm T}.\qquad
(4.16)$$

Матрица $\boldsymbol\Gamma(\mathbf y)$ может быть найдена отсюда известными методами модального управления [153]. После ее определения из (4.13), с учетом равенства $\mathbf{F=I}$, находим
$$
\boldsymbol\gamma(\mathbf{y,u})=\mathbf h_0(\mathbf{y,u}) -\boldsymbol\Gamma(\mathbf y)\mathbf g_0(\mathbf{y,u}).
$$

Таким образом, при выполнении условий (4.11), (4.15) уравнение наблюдателя для системы (4.1) имеет вид
$$
\begin{split}
\dot{\mathbf z} &=\mathbf{Lz -L}\int\limits_0^{\mathbf y}\boldsymbol\Gamma(\mathbf y)d\mathbf y -\mathbf h_0(\mathbf{y,u}) +\boldsymbol\Gamma(\mathbf y)\mathbf g_0(\mathbf{y,u});\\
\hat{\mathbf v} &=\int\limits_0^{\mathbf y}\boldsymbol\Gamma(\mathbf y)d\mathbf y -\mathbf z,
\end{split}\qquad
(4.17)$$где матрица $\boldsymbol\Gamma(\mathbf y)$ однозначно определяется уравнением (4.16) для заданного спектра матрицы $\mathbf L$. Условие (4.15) может быть использовано в качестве критерия наблюдаемости систем вида (4.1), (4.11).

4.1.4. Управление при неполной информации о векторе состояния

Предположим, что уравнения объекта имеют вид
$$
\begin{split}
\dot{\mathbf x} &=\mathbf{f(x,u)};\\
\mathbf y &=\mathbf{c(x)},
\end{split}\qquad
(4.18)$$

где $\mathbf x$ — вектор состояния; $\mathbf u$ — вектор управления; $\mathbf y$ — вектор наблюдаемых переменных. Векторы $\mathbf{f(x,u)}$ и $\mathbf{c(x)}$ предполагаются непрерывными и дифференцируемыми.

Задача заключается в синтезе динамического регулятора вида
$$
\begin{split}
\dot{\mathbf z} &=\mathbf{R(y,z)};\\
\mathbf u &=\mathbf{u(y,z)},
\end{split}\qquad
(4.19)$$

где $\mathbf z$ — вектор состояния, обеспечивающего асимптотическую устойчивость системы (4.18)—(4.19) в целом с заданным временем переходных процессов в ней.

Для решения данной задачи предположим сначала, что $\mathbf{y=x}$, и система (4.18) вполне управляема. Требуемое при этом управление $\mathbf{u(x)}$ найдем методом инвариантных многообразий, подробно рассмотренном в предыдущих главах.

Выберем далее вектор $\mathbf v$, такой, что
$$
\big|\mathbf y^{\mathrm T}\vdots \mathbf v^{\mathrm T}\big|^{\mathrm T}=\boldsymbol\alpha(\mathbf x)
$$и отображение
$$
\boldsymbol\alpha:\mathbf x \mapsto \boldsymbol\alpha(\mathbf x)
$$

взаимно однозначно для всех $\mathbf x\in\mathcal{R}^{n+m}$. Полагая в (4.18)
$$
\mathbf x=\boldsymbol\alpha^{-1}(\mathbf {y,v}),
$$

получим систему вида (4.1).

Затем методом, изложенным в п.п. 4.1.2, построим наблюдатель, формирующий оценку вектора $\mathbf v$, которую определим из уравнения (4.10). И, наконец, полагая в найденном управлении по состоянию
$$
\mathbf x=\boldsymbol\alpha^{-1}(\mathbf {y,\hat v}),
$$

получим искомые уравнения динамического регулятора вида (4.19).

По построению наблюдатель обеспечивает асимптотическое отслеживание вектора $\mathbf v$. Исключением может быть случай, когда решения системы (4.1) “уходят” в бесконечность за конечное время. Такие патологические ситуации мы здесь не рассматриваем. В остальных случаях асимптотическая устойчивость в целом замкнутой системы с динамическим регулятором, построенным предлагаемым методом, очевидно, гарантируется.

Для иллюстрации метода рассмотрим два конкретных примера.

Пример 1

Стабилизация математического маятника в верхнем неустойчивом положении.

Модель объекта имеет следующий вид:
$$
\begin{split}
\dot x_1(t) &=x_2;\\
\dot x_2(t) &=\sin x_1 +x_3;\\
\dot x_3(t) &=u;\\
y &=x_1.
\end{split}
$$

Объект удовлетворяет условию (4.1), при этом
$$
\mathbf g_0=0; \quad \mathbf G_1=\begin{vmatrix}1 & 0\end{vmatrix}; \quad \mathbf h_0=\begin{vmatrix} \sin\mathbf y\\ u\end{vmatrix}; \quad \mathbf H_1=\begin{vmatrix} 0 & 1\\0 & 0\end{vmatrix}; \quad m=2.
$$

Проверяем выполнение условия (4.15):
$$
\mathrm{rang}\big|\mathbf G_1^{\mathrm T} \vdots \mathbf H_1^{\mathrm T}\mathbf G_1^{\mathrm T}\big|=\mathrm{rang}\begin{vmatrix} 1 & 0\\ 0 & 1\end{vmatrix} =2=m.
$$

Следовательно, задача имеет решение. Уравнение (4.16) в данном случае примет вид
$$
\begin{bmatrix}0 &0\\1 &0\end{bmatrix} -\begin{bmatrix}1 \\0\end{bmatrix}\boldsymbol\Gamma^{\mathrm T}=\mathbf L^{\mathrm T}.
$$

Выбирая собственные значения матрицы $\mathbf L$ $\lambda_1=\lambda_2=-1$, находим \mathbfox{$\boldsymbol \Gamma=\begin{bmatrix}2 & 1\end{bmatrix}^{\mathrm T}$}. При этом
$$
\mathbf L=\begin{bmatrix}-2 & 1\\ -1 & 0\end{bmatrix}.
$$

Полагая в управлении по состоянию $x_1=y$, $x_2=\hat v_1$, $x_3=\hat v_2$ и используя (4.17), получаем искомые уравнения динамического регулятора:
$$
\begin{split}
\dot z_1(t) = &-2z_1 +z_2 +3y -\sin y;\\
\dot z_2(t) = &-(4 +12y^2 +\cos y)z_1 -3(1+y^2)z_2 +12 y +30y^3 +2y\cos y+\\
&+6(2y -z_1)^2y +3(1+y^2)\sin y;\\
u = &(3+12y^2 +\cos y)z_1 +3(1+y^2)z_2 -10y -30y^3 -2y\cos y-\\
&-6(2y -z_1)^2y -3(1+y^2)\sin y.
\end{split}
$$

Результаты моделирования замкнутой системы на ЭВМ при начальных условиях $x_1(0)=1$; $x_2(0)=-1$; $x_3(0)=0,5$; $z_1(0)=z_2(0)=0$ представлены на рис. 4.1.

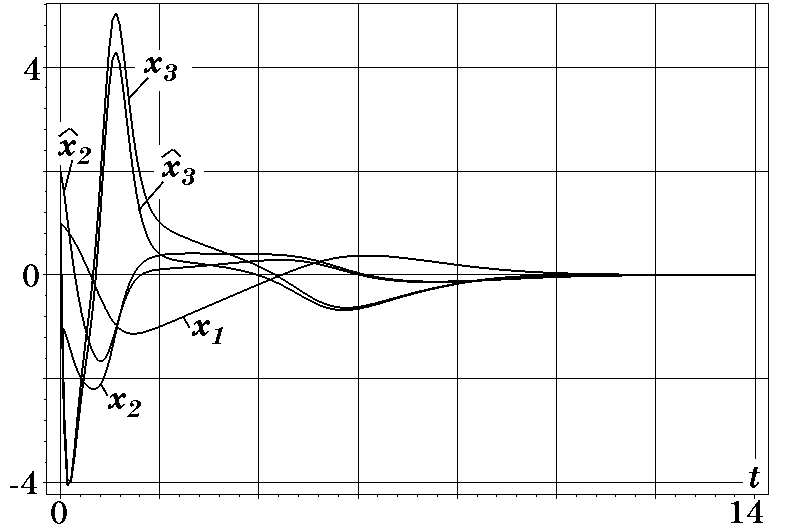
Рис. 4.1. Графики изменения координат и их оценок

Пример 2

Представим математическую модель объекта:
$$
\begin{split}
\dot x_1(t) &=x_1 +x_2;\\
\dot x_2(t) &=x_2^2 +u;\\
y &=x_1.
\end{split}
$$

Построим наблюдатель. В данном случае $\mathrm g(y,v,u)=y+v$, $\mathrm h(y,v,u)=y^2+u$. Объект не удовлетворяет условию (4.11), поэтому для построения наблюдателя используем уравнение (4.6), которое в рассматриваемом случае имеет вид
$$
\frac{\partial\varphi}{\partial y}(y+v) +\frac{\partial\varphi}{\partial v}(v^2+u)-\mathrm L(y)\varphi=\Gamma(y)(y+v) +\gamma(y,u).
$$

Положим
$$
\varphi=\varphi_1(y)v.
$$

Тогда уравнение примет вид
$$
\frac{\partial\varphi_1}{\partial y}v(y+v) +\varphi_1(v^2+u)-\mathrm L(y)\varphi_1 v=\Gamma(y)(y+v) +\gamma(y,u).
$$

Приравнивая коэффициенты при одинаковых степенях слева и справа данного равенства, приходим к системе уравнений:
$$
\begin{split}
\frac{\partial\varphi_1}{\partial y} &+\varphi_1=0;\\
\frac{\partial\varphi_1}{\partial y}y &-\mathrm L(y)\varphi_1 =\Gamma(y);\\
\Gamma(y)y &+\gamma(y,u)=\varphi_1 u.
\end{split}
$$
Из первого уравнения находим $\varphi_1=e^{-y}$. Полагая $\mathrm L(y)=-1$ из второго и третьего уравнений получаем
$$
\begin{split}
\Gamma(y) &=e^{-y}(1-y);\\
\gamma(y,u) &=-e^{-y}(1-y)y +e^{-y}u.
\end{split}
$$
При этом

$$
\int\limits_0^y\Gamma(y)dy=e^{-y}y.
$$

Полагая в найденном уравнении по состоянию $x_1=y$, $x_2=\hat v$ и используя (4.7), (4.10), получаем искомые уравнения динамического регулятора:
$$
\begin{split}
\dot z(t) &=-4z +e^{-y}(9-y)y +e^{y}(y-e^yz)^2;\\
u &=-7y +3e^yz-(y-e^yz)^2.
\end{split}
$$

Результаты моделирования замкнутой системы на ЭВМ при начальных условиях $x_1(0)=1$; $x_2(0)=2$; $z(0)=0$ представлены на рис. 4.2.

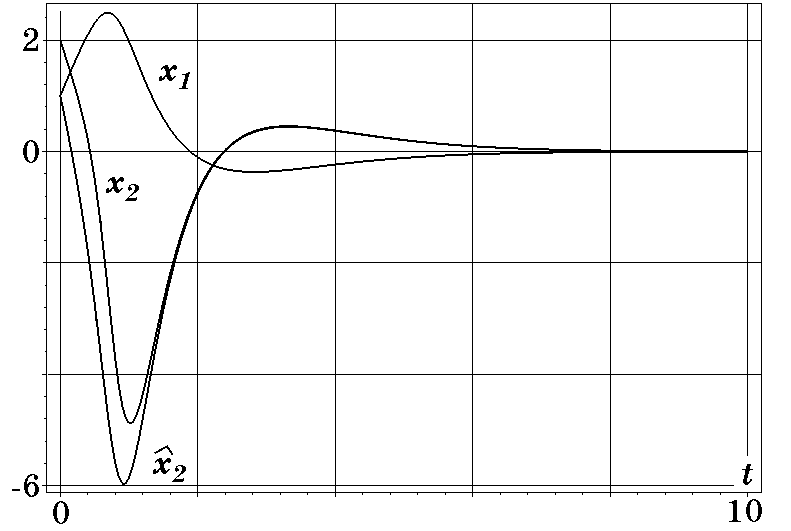
Рис. 4.2. Графики изменения координат и оценки

Перейдем к применению развитого выше синергетического метода синтеза наблюдателей к решению важных прикладных задач управления [111, 112].