Модуль 3. Синергетический синтез векторных регуляторов

3.2. Примеры аналитического конструирования векторных регуляторов для нелинейных многосвязных объектов

Покажем простоту, наглядность и эффективность метода АКАР на примерах решения сложных задач векторного управления технологическими объектами и космическими летательными аппаратами.

Пример 1

Аналитическое конструирование системы управления технологическим объектом.

Этот объект (рис. 3.1) состоит из трех конических резервуаров со свободным истечением жидкости из общего трубопровода, соединяющего выходы резервуаров. В резервуары жидкости поступают по двум каналам питания, при этом одна жидкость подается в первый и второй, а другая — в первый и третий резервуары. Управление уровнями жидкостей во втором и третьем резервуарах производится изменением потока жидкостей по первому $u_1$ и второму $u_2$ питающим трубопроводам. Расход жидкостной смеси на выходе определяется уровнем жидкости во втором резервуаре.

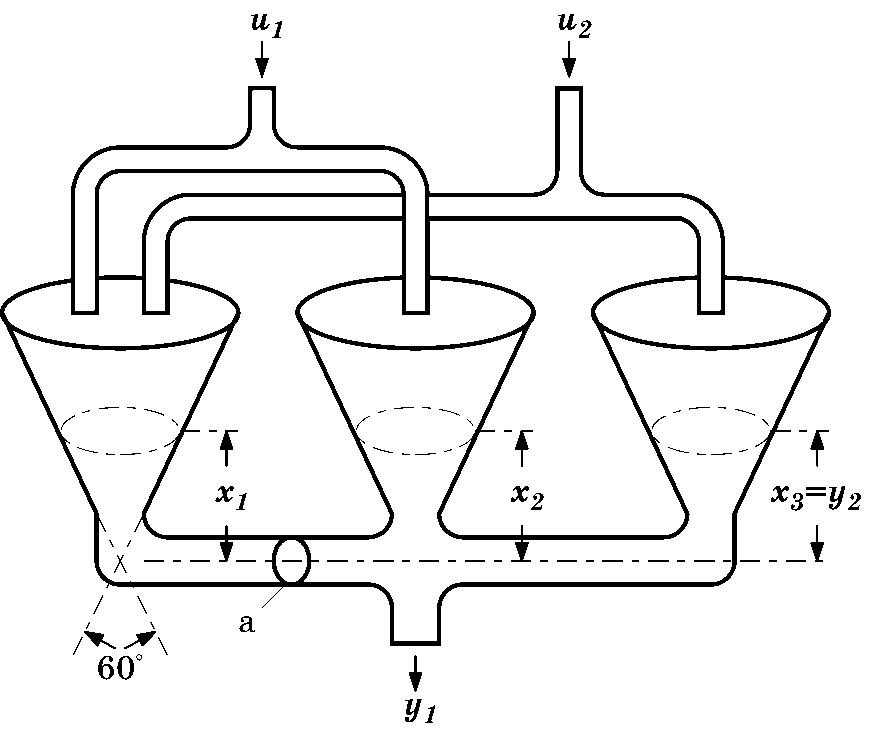
Рис. 3.1. Технологическая схема объекта управления

Система дифференциальных уравнений объекта имеет следующий вид [89]:
$$
\begin{split}
\dot x_1(t) &= -\frac{3a}{\pi x_1^2}\mathrm f(x_1-x_2) +\frac{3}{2\pi x_1^2}(u_1 +u_2);\\
\dot x_2(t) &= \frac{3a}{\pi x_2^2}\big[\mathrm f(x_1-x_2)-\mathrm f(x_2-x_3)-\mathrm f(x_2)\big]+\frac{3}{2\pi x_2^2}u_1;\\
\dot x_3(t) &= \frac{3a}{\pi x_3^2}\mathrm f(x_2-x_3) +\frac{3}{2\pi x_3^2}u_2,
\end{split}\qquad
(3.13)$$где $\mathrm f(x_i-x_j)=\sqrt{2g|x_i-x_{i+1}|}\mathrm{sign}(x_i-x_{i+1})$; $x_1,x_2,x_3$ — соответственно уровни жидкостей в первом, втором и третьем резервуарах; $y_1=a\sqrt{2gx_2}$ — расход жидкости на выходе объекта.

Сформулируем задачу синтеза двухканального регулятора: требуется методом АКАР определить законы управления $u_1$, $u_2$, обеспечивающие заданные уровни жидкостей во втором и третьем резервуарах и, следовательно, заданный расход жидкости на выходе, т.е.
$$
x_2=x_{2r}=\frac{y_{1r}^2}{2ga^2}; \quad x_3=x_{3r}=y_{2r}; \quad x_{1r}=1,25 x_{2r}.\qquad
(3.14)$$В установившемся режиме согласно (3.14) выполняются следующие соотношения:
$$\begin{split}
\mathrm f(x_{1r} -x_{2r}) &=0,5\mathrm f(x_{2r});\\
a\mathrm f(x_{2r}) &= u_{1r} +u_{2r}=y_{1r};\\
a\mathrm f(x_{2r} -x_{3r}) &=-0,5u_{2r}.
\end{split}\qquad
(3.15)$$По заданному $x_{2r}$ (3.14) из (3.15) можно найти $x_{1r}$ — уровень жидкости в первом резервуаре в установившемся режиме работы объекта. Отличительной особенностью объекта (3.13) с точки зрения АКАР является присутствие управлений $u_1$ и $u_2$ во всех строках правых частей дифференциальных уравнений. Согласно методу АКАР, управления $u_1$ и $u_2$ всегда можно синтезировать так, чтобы обязательно обеспечить требуемые соотношения (3.14). Что же касается координаты $x_1$, то ее поведение будет определяться свойствами первого дифференциального уравнения системы (3.13) после подстановки в него синтезированных управлений.

Перейдем к изложению процедуры синтеза двухканального агрегированного регулятора для нелинейного технологического объекта (3.13). Согласно методу АКАР, введем, например, следующие линейные макропеременные:
$$
\begin{split}
\psi_1 &=\alpha_2(x_2 -x_{2r}) +\alpha_3(x_3 -x_{3r});\\
\psi_2 &=\beta_2(x_2 -x_{2r}) +\beta_3(x_3 -x_{3r}).
\end{split}\qquad
(3.16)$$Синтезируемые управления $u_1$ и $u_2$ должны переводить изображающую точку объекта из произвольного начального состояния на пересечение $\psi_{12}=0$ многообразий $\psi_1=0$ и $\psi_2=0$ (3.16). Указанное пересечение можно записать в виде следующих двух уравнений:
$$B(x_2 -x_{2r})=0; \quad B(x_3 -x_{3r})=0,\qquad
(3.17)$$где $B=\alpha_2\beta_3 -\beta_2\alpha_3$, $B\neq 0$. Полученные соотношения (3.17) совпадают с выражениями (3.14), т.е. выбранные макропеременные $\psi_1$ и $\psi_2$ (3.16) обеспечивают заданные требования к системе управления объектом в установившемся режиме работы. Для синтеза управлений $u_1(x_1,x_2,x_3)$ и $u_2(x_1,x_2,x_3)$ подставим макропеременные $\psi_1$ и $\psi_2$ (3.16) в функциональные уравнения
$$
T_1\dot\psi_1(t) +\psi_1=0; \quad T_2\dot\psi_2(t) +\psi_2=0; \quad T_1>0; \quad T_2>0,\qquad
(3.18)$$тогда в силу уравнений объекта (3.13) получим
$$
u_1 =-2a\big[\mathrm f(x_1-x_2) {-}\mathrm f(x_2-x_3) {-}\mathrm f(x_2)\big] {-}\frac{2\pi \beta_3 x_2^2}{3T_1B}\psi_1 {+}\frac{3\pi \alpha_3 x_2^2}{3T_2 B}\psi_2;\qquad
(3.19)$$
$$
u_2=-2a\mathrm f(x_2-x_3) +\frac{2\pi \beta_2 x_3^2}{2T_1B}\psi_1 -\frac{2\pi \alpha_2 x_3^2}{3T_2 B}\psi_2\qquad
(3.20)$$Подставив макропеременные $\psi_1$ и $\psi_2$ (3.16) в выражения (3.19) и (3.20), после преобразований получим следующие законы двухканального взаимосвязанного управления:
$$
\begin{split}
u_1 &= -2a\big[\mathrm f(x_1-x_2) {-}\mathrm f(x_2-x_3) {-}\mathrm f(x_2)\big] {-}\frac{2\pi x_2^2}{3B}\left(\frac{\alpha_2\beta_3}{T_1}{-}\frac{\alpha_3\beta_2}{T_2}\right)\times\\
&\times
(x_2-x_{2r}) -\frac{2\pi x_2^2\alpha_3\beta_3}{3B}\left(\frac{1}{T_1} -\frac{1}{T_2}\right)(x_3 -x_{3r});
\end{split}\qquad
(3.21)$$
$$
\begin{split}
u_2=&-2a\mathrm f(x_2-x_3)-\frac{2\pi x_3^2}{3B}\left(\frac{\alpha_2\beta_3}{T_2}-\frac{\alpha_3\beta_2}{T_1}\right)(x_3 -x_{3r})-\\
& -\frac{2\pi x_3^2\alpha_2\beta_2}{3B}\left(\frac{1}{T_2} -\frac{1}{T_1}\right)(x_2-x_{2r}).
\end{split}\qquad
(3.22)$$Управления $u_1$ (3.19) и $u_2$ (3.20) или $u_1$ (3.21) и $u_2$ (3.22) обеспечивают асимптотически устойчивое движение изображающей точки сначала к пересечению многообразий $\psi_{12}=0$ (3.17), а затем вдоль $\psi_{12}=0$, когда $\psi_1=\psi_2=0$, т.е. $x_2=x_{2r}$, $x_3=x_{3r}$. Поведение координаты $x_1$ при движении вдоль $\psi_{12}=0$ будет определяться первым дифференциальным уравнением системы (3.13), которое после подстановки $u_1$ и $u_2$ принимает вид
$$
\dot x_1(t)=-\frac{6a}{\pi x_1^2}\big[\mathrm f(x_{2r}-x_1)-0,5\mathrm f(x_{2r})\big].\qquad
(3.23)$$Исследуем устойчивость уравнения (3.23) относительно установившегося значения координаты $x_1=x_{1r}$. Для этого введем определенно положительную функцию Ляпунова
$$
v(t)=0,5(x_1-x_{1r})^2.\qquad
(3.24)$$Тогда полная производная $\dot v(t)$ (3.24) по времени в силу уравнения (3.23) будет иметь вид
$$
\dot v(t)=-\frac{6a(x_1-x_{1r})}{\pi x_1^2}\big[\mathrm f(x_1-x_{2r})-0,5\mathrm f(x_{2r})\big].\qquad
(3.25)$$По физическим требованиям к функционированию объекта условие $x_1>0$ всегда соблюдается. Рассмотрим теперь условия обеспечения знакоотрицательности функции $\dot v(t)$ (3.25), что определяется знаком произведения выражений $(x_1-x_{1r})$ и $\big[\mathrm f(x_1-x_{2r})-0,5\mathrm f(x_{2r})\big]$ в правой части уравнения (3.25). Тогда с учетом первого соотношения (3.15) имеем следующие два возможных варианта:
$$
\sqrt{2g(x_1 -x_{2r})} -0,5\sqrt{2g|x_{2r}|}>0 \; \text{при}\; x_1>x_{1r}\;\text{т.е. при}\;(x_1 -x_{1r})>0\qquad
(3.26)$$и
$$
\sqrt{2g(x_1 -x_{2r})} -0,5\sqrt{2g|x_{2r}|}<0 \; \text{при}\; x_1<x_{1r}\;\text{т.е. при}\;(x_1 -x_{1r})<0.\qquad
(4.27)$$В обоих вариантах (3.26) и (3.27) обеспечиваются условия знакоотрицательности функции $\dot v(t)<0$ (3.25), что означает асимптотическую устойчивость в целом уравнения (3.23) относительно положения равновесия $x_1=x_{1r}$. Следовательно, синтезированные законы управления $u_1$ (3.21) и $u_2$ (3.22) обеспечивают асимптотическую устойчивость движения в целом замкнутой системы относительно заданного состояния (3.14), определяемого требованиями технологического процесса.

Рассмотрим теперь некоторые свойства замкнутой системы (3.13), (3.21), (3.22). Из выражений для законов управлений $u_1$ (3.21) и $u_2$ (3.22) следует, что взаимное влияние между каналами управления определяется функцией $\mathrm f(x_2-x_3)$ и последними членами:
$$
\frac{2\pi x_2^2\alpha_3\beta_3}{3B}\left(\frac{1}{T_1} -\frac{1}{T_2}\right)(x_3 -x_{3r}) \;\;\text{и}\;\;\frac{2\pi x_3^2\alpha_2\beta_2}{3B}\left(\frac{1}{T_2} -\frac{1}{T_1}\right)(x_2-x_{2r}).\qquad
(3.28)$$Если положить в (3.28) постоянные времени $T_1=T_2=T$, то тогда управления $u_1$ и $u_2$ принимают вид
$$
\begin{split}
u_1 &=-2a\big[\mathrm f(x_1-x_2) -\mathrm f(x_2-x_3) -\mathrm f(x_2)\big] -\frac{2\pi x_2^2}{3T}(x_2-x_{2r});\\
u_2 &=-2a\mathrm f(x_2-x_3)-\frac{2\pi x_3^2}{3T}(x_3 -x_{3r}).
\end{split}\qquad
(3.29)$$Отличие управлений (3.29) от (3.21) и (3.22) состоит в том, что в них исчезли дополнительные каналы взаимного влияния (3.28), полученные в результате применения метода АКАР, и, кроме того, в (3.29) теперь отсутствуют параметры $\alpha_2$, $\alpha_3$, $\beta_2$ и $\beta_3$, соответствующим выбором которых можно придать дополнительные свойства взаимосвязанной системе управления объектом (3.13). Подставив (3.29) в (3.13), получим для координат следующие уравнения:
$$
\begin{split}
\dot x_2(t) &=-\frac{1}{T}(x_2 -x_{2r});\\
\dot x_3(t) &=-\frac{1}{T}(x_3 -x_{3r}).
\end{split}
(3.30)$$Дифференциальные уравнения (3.30) являются автономными, однако их решения согласованы друг с другом по времени переходных процессов. Итак, при выполнении равенства $T_1=T_2=T$ управления $u_1$ (3.21) и $u_2$ (3.22) обеспечивают, помимо асимптотической устойчивости движения в целом замкнутой системы, также автономность координат $x_2$ и $x_3$ и, согласно (3.31), апериодический характер затухания переходных процессов. Интересно, что при этом для нелинейной замкнутой системы (3.13), (3.21), (3.22) можно указать время регулирования $t_p\approx 3T$ для произвольного начального состояния.

Результаты моделирования замкнутой системы (3.13), (3.21), (3.22) при $T_1=T_2=1$, $x_{1r}=12,5$, $x_{2r}=10$, $x_{3r}=5$, $a=2$ приведены на рис. 3.2.

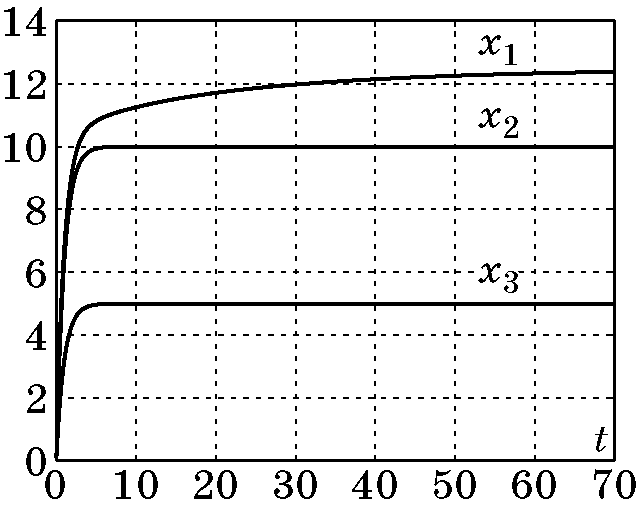
Рис. 3.2. Результаты моделирования замкнутой системы

Отметим, что в работе [89] на основе функций Ляпунова получены законы управления $u_1$ и $u_2$, которые точно совпадают с $u_1$ и $u_2$ (3.29) для рассмотренного частного случая, когда выполняется условие $T_1=T_2=T$. Разумеется, что синтезированные методом АКАР управления (3.21) и (3.22) в большей мере учитывают взаимное влияние каналов управления, что может оказаться важным, в частности, при действии неучтенных возмущений на объект. Кроме того, в случае необходимости путем соответствующего выбора нелинейных макропеременных $\psi_1$ и $\psi_2$ можно придать системе дополнительные желаемые свойства переходных процессов.

pr32_2pr32_2Пример 2

Аналитическое конструирование нелинейной системы управления вращением спутника, движение которого описывается следующей системой нелинейных дифференциальных уравнений [152]:
$$
\begin{split}
\dot x_1(t) &=-2x_2 +u_1;\\
\dot x_2(t) &=2x_1 +u_2;\\
\dot x_3(t) &=-x_2\omega(x_3,x_4) +x_4;\\
\dot x_4(t) &=x_1\omega(x_3,x_4) -x_3,
\end{split}\qquad
(3.31)$$где $\omega(x_3,x_4)=\big(1-x_3^2 -x_4^2\big)^{1/2}$; координаты $x_1$, $x_2$ — компоненты спин-вектора; координаты $x_3$, $x_4$ — компоненты вспомогательного вектора единичной длины, возникающие при переходе к инерциальной системе координат из системы, жестко связанной со спутником; управления , $u_1$, $u_2$ — моменты, создаваемые двумя реактивными двигателями.

Необходимо синтезировать законы управления $u_1(x_1,\dots,x_4)$ и $u_2(x_1,\dots,x_4)$, т.е. осуществить аналитическое конструирование автопилота, обеспечивающего стабилизацию вращения спутника вокруг неподвижной оси. Заметим, что по определению область изменения координат $x_3$ и $x_4$ спутника удовлетворяет неравенству $x_3^2 +x_4^2<1$, поэтому поведение этих координат следует рассматривать в указанной области.

Первый вариант синтеза

Покажем, что, применяя разработанный метод АКАР, можно путем весьма простых аналитических процедур синтезировать автопилот, который не только гарантирует асимптотическую устойчивость движения спутника (3.31) в заданной области $\big(x_3^2 +x_4^2<1\big)$, но и обеспечивает желаемые характер и время переходных процессов. Для этого введем следующие агрегированные макропеременные:
$$
\begin{split}
\psi_1 &=x_1 +\beta_{12}x_2 +\beta_{13}x_3\omega^{-1};\\
\psi_2 &=x_1 +\beta_{2}2x_2 +\beta_{2}4x_4\omega^{-1}
\end{split}\qquad
(3.32)$$Применяя функциональные уравнения

$$
T_1\dot\psi_1(t) +\psi_1=0; \quad T_2\dot\psi_2(t) +\psi_2=0; \quad T_1>0; \quad T_2>0,
$$

найдем законы управления:
$$
\begin{split}
Bu_1 {=} &{-}\Bigg(\frac{\beta_{22}}{T_1} {-}\frac{\beta_{12}}{T_2}{-}\beta_{24}\beta_{12}\Bigg)x_1
{+}\Bigg(\frac{\beta_{22}\beta_{12}}{T_2} {+} 2B {+}\beta_{13}\beta_{22}{-}\frac{\beta_{12}\beta_{22}}{T_1}\Bigg)x_2{+}\\
&+\big(\beta_{12}\beta_{22}x_3 -\beta_{24}\beta_{12}x_4\big)
\times\big(x_2x_3-x_1x_4\big)\omega^{-2}-\\
&-\Bigg(\beta_{24}\beta_{22} +\frac{\beta_{22}\beta_{13}}{T_1}\Bigg)x_3\omega^{-1}
-\Bigg(\beta_{13}\beta_{22} -\frac{\beta_{12}\beta_{24}}{T_2}\Bigg)x_4\omega^{-1};
\end{split}\qquad
(3.33)$$

$$
\begin{split}
Bu_2 {=} &{-}\Bigg(2B {+}\beta_{24} {-}\frac {1}{T_1} {+}\frac {1}{T_2}\Bigg)x_1 {-}\Bigg(\beta_{13} {+}\frac{\beta_{22}}{T_2} {-}\frac{\beta_{12}}{T_1}\Bigg)x_2 %+\\
{+} \Bigg(\beta_{24} {+}\frac{\beta_{13}}{T_1}\Bigg)x_3\omega^{-1}{+} \\
&+\Bigg(\beta_{13} +\frac{\beta_{24}}{T_2}\Bigg)x_4\omega^{-1}%+\\
+\big(\beta_{13}x_3 -\beta_{24}x_4\big)\big(x_1x_4 -x_2x_3\big)\omega^{-2},
\end{split}\qquad
(3.34)$$где $B=\beta_{22} -\beta_{12}$, $\omega=\big(1-x_3^2-x_4^2\big)^{1/2}$.
Управления $u_1$ (3.33) и $u_2$ (3.34) обеспечивают перевод ИТ замкнутой системы (3.13), (3.15), (3.16) на пересечение многообразий:
$$
\begin{split}
\psi_1 &=x_1 +\beta_{12}x_2 +\beta_{13}x_3\omega^{-1}=0;\\
\psi_2 &=x_1 +\beta_{22}x_2 +\beta_{24}x_4\omega^{-1}=0.
\end{split}\qquad
(3.35)$$

Находя из совместного решения уравнений (3.35) координаты $x_1$ и $x_2$ и подставляя их соответственно в первое и второе уравнения системы (3.31), получаем дифференциальные уравнения
$$
\begin{split}
\dot x_{3\psi 12}(t)= &-\frac{\beta_{13}}B x_{3\psi 12} +\Bigg(1+\frac{\beta_{24}} B\Bigg)x_{3\psi 12};\\
\dot x_{4\psi 12}(t)= &-\Bigg(1+\frac{\beta_{13}\beta_{22}} B\Bigg) x_{3\psi 12}+\frac{\beta_{24}\beta_{12}} B x_{4\psi 12},
\end{split}\qquad
(3.36)$$которые описывают движение ИТ вдоль пересечения многообразий $\psi_{12}=0$. Система уравнений (3.36) является линейной, а условия ее устойчивости имеют вид
$$
\beta_{22}>0; \quad \beta_{24}>0; \quad \beta_{12}<0;\quad \beta_{13}>0.\qquad
(3.37)$$Таким образом, законы управления (3.33) и (3.34) при выполнении простейших неравенств (3.37) гарантируют синтезированной системе асимптотическую устойчивость в целом по координатам $x_1$, $x_2$ и асимптотическую устойчивость в области $x_3^2+x_4^2<1$ по координатам $x_3$ и $x_4$. Выбор параметров $\beta_{1i}$ и $\beta_{2i}$ может производиться из условий оптимизации системы в режиме малых отклонений по некоторому квадратичному критерию качества или исходя из задания прямых показателей качества, например времени и характера затухания переходных процессов системы (3.36), описывающей движение ИТ вдоль пересечения многообразий $\psi_{1-2}=0$ к началу координат фазового пространства.

На ЭВМ было выполнено моделирование синтезированной системы стабилизации вращения спутника с законами управления (3.33) и (3.34). При этом были выбраны следующие параметры: $\beta_{22}=1$; $\beta_{24}=1$; $\beta_{12}=-1$; $\beta_{13}=10$; $B=2$; $T_1=T_2=0,5$. На рис. 3.3 приведены графики изменения координат $x_1(t),\dots,x_4(t)$, а на рис. 3.4 — управлений $u_1$, $u_2$ и макропеременных $\psi_1(t)$, $\psi_2(t)$ для начальных условий $x_{10}=\dot x_{20}=1,0$; $x_{30}=0,6$; $x_{40}=0,5$.

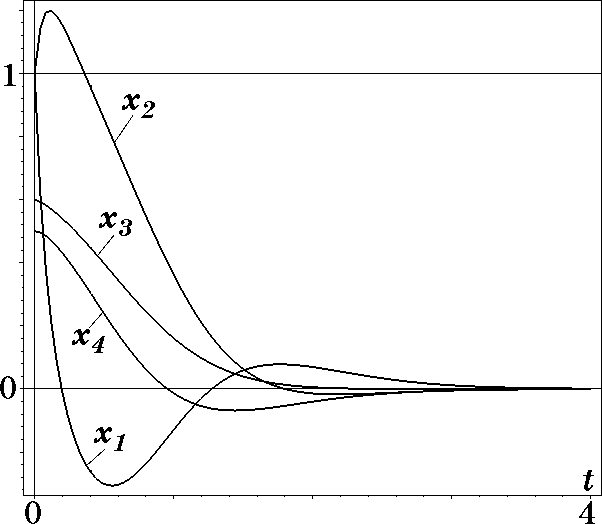
Рис. 3.3. Графики изменения координат

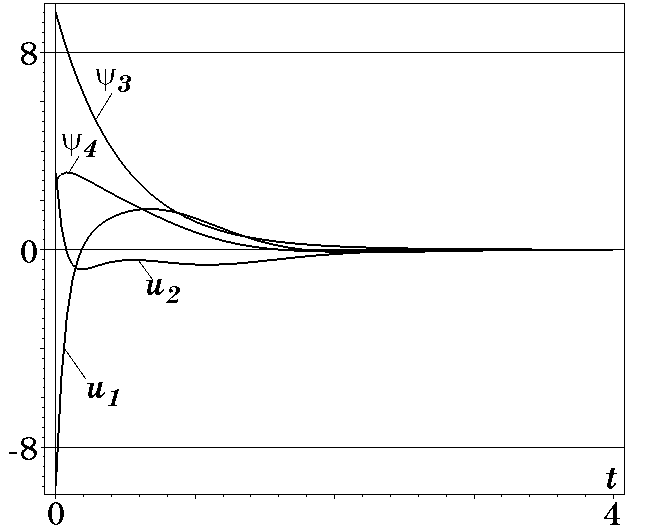
Рис. 3.4. Графики изменения управлений и макропеременных

Из рис. 4.3 и рис. 4.4 видно, что синтезируемая нелинейная система стабилизации спутника является асимптотически устойчивой, переходные процессы близки к апериодическим, т.е. результаты моделирования в полной мере согласуются с теоретическими положениями разработанного метода АКАР с несколькими управлениями.

Второй вариант синтеза

Полученные на основе макропеременных $\psi_1$ и $\psi_2$ (3.32) законы $u_1$ (3.33), $u_2$ (3.44) управления вращением спутника обеспечивают при выполнении условий (3.37) асимптотическую устойчивость движения и апериодический характер переходных процессов. Однако эти законы при $x_1^2+x_3^2\approx 1$ и, следовательно, $\omega\approx 0$ имеют особенность, приводящую к резкому возрастанию управлений. Для того, чтобы избежать указанную особенность и упростить реализацию законов управления, введем в рассмотрение макропеременные следующего вида:
$$
\begin{split}
\psi_3 &=\gamma_1 x_1 +\gamma_2 x_2 +\gamma_3 x_3 +x_4 +\gamma_4 x_3^3 +\gamma_5 x_4^3;\\
\psi_4 &=\rho_1 x_1 +\rho_2 x_2 +\rho_3 x_3 +x_4 +\rho_4 x_3^3 +\rho_5 x_4^3.
\end{split}
$$Тогда, подставляя эти макропеременные в функциональные уравнения
$$
T_3\dot\psi_3(t) +\psi_3=0; \quad T_4\dot\psi_4(t) +\psi_4=0; \quad T_3>0; \quad T_4>0,
$$найдем в силу исходных уравнений объекта (3.31) законы управления
$$
u_3=2x_1 -\frac 1{\gamma_1}\big(1+3\gamma_5x_4^2\big)(x_1\omega -x_3) -\frac{\rho_2}{B_1\gamma_1T_3}\psi_3 +\frac{\gamma_2}{B_1\gamma_1T_4}\psi_4;\qquad
(3.38)$$
$$
u_4=-2x_1 -\big[\gamma_3 -\rho_3 +3(\gamma_4 -\rho_4)x_3^2\big](x_2\omega -x_3) +\frac 1{T_3}\psi_3 -\frac 1{T_4}\psi_4.\qquad
(3.39)$$Полученные законы управлений $u_3$, $u_4$ (3.38), (3.39) в отличие от законов $u_1$ (3.33), $u_2$ (3.34) уже не имеют описанной ранее особенности и обеспечивают перевод ИТ в окрестность пересечений многообразий $\psi_3=0$ и $\psi_4=0$. Движение ИТ вдоль пересечения $\psi_{34}=0$ описывается нелинейными дифференциальными уравнениями:
$$
\begin{split}
\dot x_{3\psi 34}(t) &=-\big(\beta_1 x_{3\psi 34}+\beta_2x_{3\psi 34}^3\big)\omega +x_{4\psi 34};\\
\dot x_{4\psi 34}(t) &=-\big(\alpha_1x_{4\psi 34} +\alpha_2x_{4\psi 34}^3\big)\omega -x_{3\psi 34}.
\end{split}\qquad
(3.40)$$

Уравнения (3.40) асимптотически устойчивы относительно положения $x_{3\psi 34}=x_{4\psi 34}=0$ в области $x_3^2+x_4^2\le 1$, что можно показать на основе функции Ляпунова:
$$
\mathrm V_{\psi 34}=0,5x_{3\psi 34}^2 +0,5x_{4\psi 34}^2.
$$Полная производная этой функции по времени

$$
\dot{\mathrm V}(t)=-\big(\beta_1 x_{3\psi 34}^2+\beta_2x_{3\psi 34}^4\big)\omega -\big(\alpha_1x_{4\psi 34}^2 +\alpha_2x_{4\psi 34}^4\big)\omega <0
$$определенно отрицательна при выполнении неравенств

$$
\beta_1>0; \quad \beta_2>0; \quad \alpha_1>0; \quad \alpha_2>0,
$$что и доказывает асимптотическую устойчивость движения ИТ вдоль пересечения многообразий $\psi_{34}=0$ к началу координат. Следовательно, замкнутая управлениями $u_3$ (3.38) и $u_4$ (3.39) система будет также асимптотически устойчивой. Между коэффициентами в приведенных выше выражениях установлены следующие соотношения:
$$
\alpha_1=\frac 1{\gamma_1}; \quad \alpha_2=\frac {\gamma_5}{\gamma_1}; \quad \beta_1=\frac{\rho_3}{\rho_2}; \quad \beta_2=\frac{\rho_4}{\rho_2},
$$при этом $\gamma_1=\rho_1$; $\gamma_5=\rho_5$; $\gamma_3\rho_2=\rho_3\gamma_2$; $\gamma_4\rho_2=\rho_4\gamma_2$; $\gamma_2\neq\rho_2$.

Введенные выше макропеременные $\psi_3$ и $\psi_4$ включают в себя кубические члены $x_3^3$ и $x_4^3$ с соответствующими коэффициентами, что позволяет повысить быстродействие движения ИТ вдоль пересечения многообразий $\psi_{34}=0$. Очевидно, что эти члены можно исключить $(\gamma_4=\gamma_5=\rho_4=\rho_5=0)$ без потери асимптотической устойчивости синтезированной системы управления вращением спутника.

Покажем, что системе (3.40), описывающей движение ИТ вдоль $\psi_{34}=0$, можно дать очевидную геометрическую интерпретацию. Для этого, в частности, положив $\alpha_1=\beta_1=\alpha$; $\alpha_2=\beta_2=0$ и умножив первое уравнение системы (3..117} на $x_{3\psi}$, второе — на $x_{4\psi}$ и сложив почленно, получим
$$
\dot x_{3\psi}(t)x_{3\psi} +\dot x_{4\psi}(t)x_{4\psi}=-\alpha\big(x_{3\psi}^2 +x_{4\psi}^2\big)\big(1-x_{3\psi}^2 -x_{4\psi}^2\big)^{1/2}.
(3.41)$$Тогда, введя полярные координаты $x_3(t)=r(t)\sin\varphi(t)$; $x_4(t)=r(t)\cos\varphi(t)$ и обозначив $r^2=x_{3\psi}^2 +x_{4\psi}^2$ как расстояние от ИТ до начала координат, из (3.40), (3.41) найдем
$$\begin{split}
\dot r(t) &=-\alpha r\sqrt{1-r^2};\\
\dot\varphi(t) &=1.
\end{split}\qquad
(3.42)$$Уравнения (3.42), описывающие кинематические соотношения на $\psi_{34}=0$, имеют решения
$$
r(t)=\pm\frac 1{\sqrt{1 +ce^{\alpha t}}}; \quad \varphi(t)=\varphi_0 +t.\qquad
(3.41)$$

Из (3.43) следует, что при $\alpha>0$ и $t\to\infty$ радиус $r(t)$ на пересечении многообразий $\psi_{34}=0$ гиперболически убывает, стремясь к нулю, а при $\alpha<0$ радиус стремится к значению $r_s=1$, при этом частота вращения $\omega_0=1$. Это указывает на асимптотическую устойчивость движения ИТ вдоль $\psi_{34}=0$ и, следовательно, означает, что при $T_1>0$, $T_2>0$, $\alpha>0$ синтезированная нелинейная система управления KЛA обладает свойством асимптотической устойчивости по координатам $x_1$, $x_2$ в целом, а по координатам $x_3$, $x_4$ — в области $x_3^4 +x_4^2<1$. Результаты моделирования синтезированной системы стабилизации вращения спутника с управлениями (3.38), (3.39) представлены на рис. 3.5 и рис. 3.6.

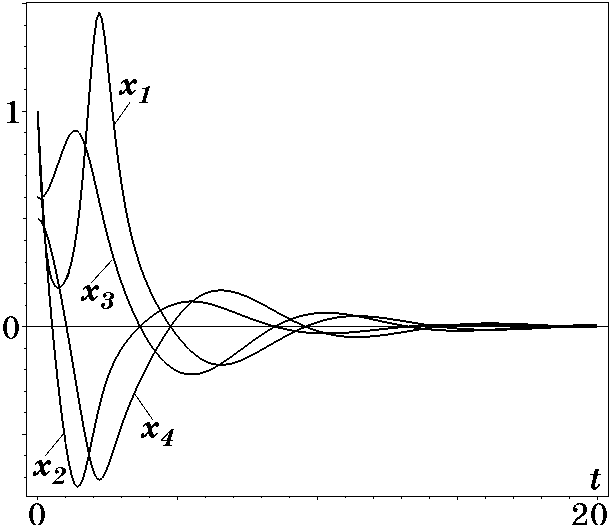
Рис. 3.5. Графики изменения координат

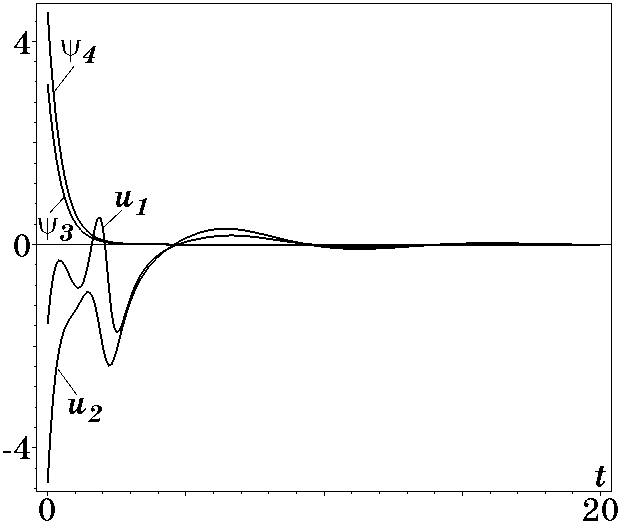
Рис. 3.6. Графики изменения управлений и макропеременных

Выявим теперь отличия между двумя вариантами синтеза автопилота. Указанные отличия в первую очередь определяются уравнениями движения ИТ вдоль пересечения выбранных многообразий. В первом варианте это были линейные дифференциальные уравнения (3.36), а во втором — нелинейные (3.40). Если в первом варианте условия устойчивости движения вдоль пересечения многообразий элементарны, то во втором для исследования асимптотической устойчивости потребовалось уже применение функций Ляпунова. Разумеется, что во втором варианте возникают более широкие возможности в отношении обеспечения желаемых динамических свойств движения спутника.
В общем же случае уравнения движения ИТ вдоль пересечения многообразий целесообразно выбирать, исходя из условий согласованности с естественными (механическими, энергетическими и т.д.) свойствами движения спутника. Это отдельный вопрос, подлежащий самостоятельному рассмотрению. Таким образом, на основе метода АКАР можно аналитически синтезировать различные двухканальные системы управления спутником.