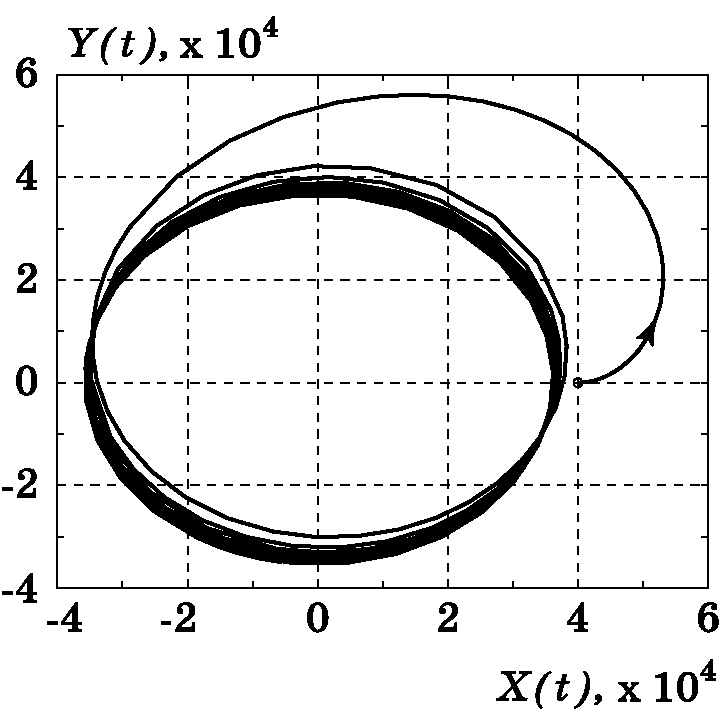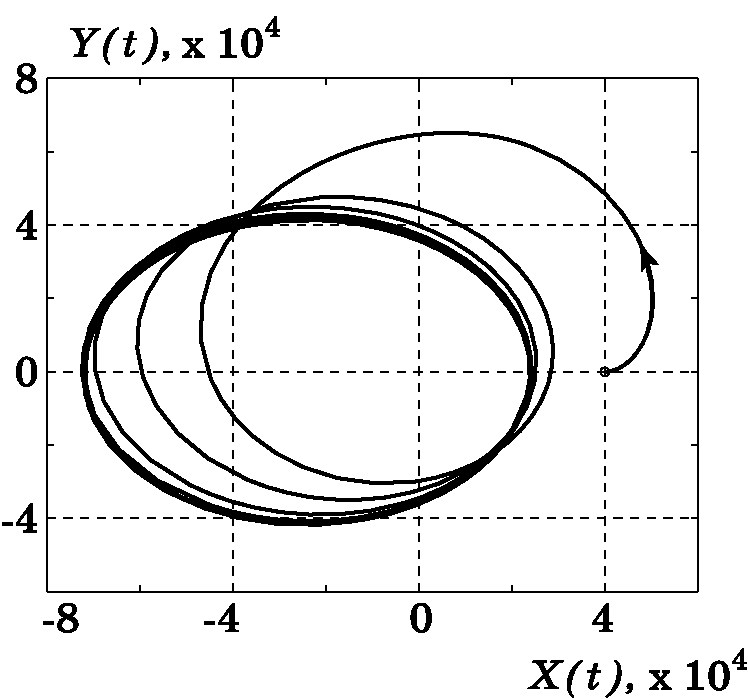Модуль 3. Синергетический синтез векторных регуляторов
3.3. Проблема синтеза естественных закономерностей: системные законы тяготения
Известно, что сущность классической механики и вообще физики определяется, в первую очередь, содержанием тех законов природы, которые описывают соответствующую предметную область. История науки показывает, что эти законы практически всегда являлись результатом догадки, прозрения и везения великих ученых. Возникает идея о своего рода синергетической генерации такого рода законов, т.е. поиска объективных закономерностей единства процессов самоорганизации и управления (взаимодействия). Разумеется, что такая постановка научной задачи в определенной мере претенциозна, однако даже первые успешные шаги в этом направлении позволили бы указать перспективный путь выявления общесистемных естественных закономерностей различной природы.
Рассмотрим следующую проблему системного синтеза: на основе известных естественных закономерностей — инвариантов, отражающих соответствующие природные взаимодействия, синтезировать новые, системные законы, позволяющие существенно расширить знание о соответствующей предметной области, например, о космонавтике, навигации, управлении пространственным движением и т.д. Системные законы имеют динамическую природу, что принципиально отличает их от известных законов физики, являющихся, как правило, статическими, т.е. описывающими лишь стационарные движения. Это означает, что системные законы включают в себя дополнительные, динамические компоненты, которые “исчезают” на стационарном движении, т.е. не наблюдаются. В этом свойстве и проявляется латентный (скрытый) характер системных законов, что ведет к возникновению неожиданных физических явлений. Отсюда вытекает возможность предсказания новых явлений и свойств соответствующих систем и, следовательно, выявления перспектив переноса естественных закономерностей на искусственные управляемые системы, обладающие принципиально новыми динамическими свойствами.
Конкретно здесь предпринята попытка на основе гравитационных инвариантов синтезировать системные законы тяготения, структурно включающие в себя известный закон Ньютона как ключевое ядро. При решении этой неординарной задачи будем опираться на синергетическую концепцию единства процессов самоорганизации и самоуправления — нелинейного взаимодействия, согласно которой формируется последовательная совокупность динамически вкладываемых друг в друга законов тяготения [61, 90].
Отметим, что в последнее время в Институте проблем управления РАН развивается системный подход к поиску новых законов и закономерностей в электродинамике, природе и обществе [91]. Это означает, что проблема синтеза системных законов тяготения, впервые рассматриваемая в наших работах [92, 93], лежит в русле указанного весьма перспективного научного направления, которое можно назвать системной физикой. Подчеркнем, что проблема построения системных закономерностей издавна была и остается одной из самых актуальнейших проблем науки. Поэтому любое продвижение в направлении ее решения имеет важное общенаучное значение.
В прикладном плане основная цель рассматриваемой здесь постановки задачи синтеза системных закономерностей тяготения состоит в выявлении возможных новых классов законов управления движением, например, космических летательных аппаратов (КЛА) с “малой тягой”, в том числе связанных с задачей об оптимальной эволюции плоской орбиты [94, 96] и др. Дело в том, что закон тяготения Ньютона описывает стационарное движение тел в слабом гравитационном поле, поэтому он используется в космонавтике в основном для расчета программных траекторий полета КЛА, в то время как на практике необходимо еще также решать задачи навигации и оптимальной стабилизации движения КЛА по соответствующей траектории или орбите в условиях действия внешних возмущений. Если удастся синтезировать такого рода естественные системные законы тяготения, то это, на наш взгляд, может открыть новые возможности как в задачах управления полетом КЛА, так и в других областях космонавтики, навигации и, вообще, управления пространственным движением. Разумеется, что для продвижения в решении этой важной прикладной проблемы потребуется даже затронуть некоторые каноны ньютоновской теории тяготения, в частности, предполагать, что гравитационное поле является активным, а начальные условия системы — произвольными, и др.
В качестве примера рассмотрим задачу управления орбитальными движениями КЛА с “малой тяги”. К настоящему времени механика полета КЛА с малой тягой превратилась в развитый самостоятельный раздел механики космического полета [94—96]. Уравнения движения КЛА в плоскости орбиты имеют следующий вид [96]:
$$
\dot r(t)=V_r, \quad \dot V_r(t)=V_\theta^2 r^{-1} - \frac{h^2}{p} r^{-2} + U_r,\qquad
(3.44)$$
$$
\dot\theta(t)=V_\theta r^{-1}, \quad \dot V_\theta(t)=-V_rV_\theta r^{-1}+ U_\theta.\qquad
(3.45)$$
Здесь обозначено: $r$, $\theta$ — полярные координаты; $V_r$, $V_\theta$ — радиальная и трансверсальная составляющие скорости; $U_r$, $U_\theta$ — составляющие вектора тяги; $\theta=\chi+\gamma$, $\chi$ — истинная аномалия, $\gamma$ — угловая постоянная, которая определяет угол между линией апсид и осью $OX$ (рис. 3.7).
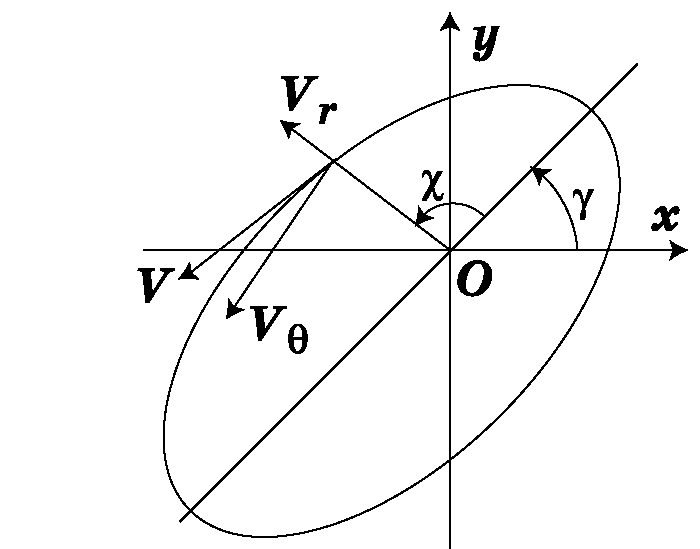
Рис. 3.7. Система координат искусственного спутника Земли
Управляющие воздействия считаются малыми по сравнению с минимальным значением силы тяготения, т.е. $\big(U_r^2 +U_\theta^2\big)^{1/2}\ll \dfrac{h^2}{pr_{\max}^{2}}$ [96]. Очевидно, что при $U_r=U_\theta= 0$ и отрицательной полной энергии $E<0$ уравнения (3.44) и (3.45) описывают движение КЛА по эллиптической орбите под действием закона тяготения Ньютона
$$
U_{rN}=U_{r\omega}-\frac{h^2}{pr^2}=-\frac{GM}{r^2}\qquad
(3.46)$$
где: $M$ — масса притягивающего центра; $m$ — масса прицельного тела; $r$ — радиус-вектор, определяющий расстояние до центра; $G$ — постоянная гравитации; \mbox{$M\gg m$}.
Иначе говоря, здесь рассматривается проблема системного синтеза новых объективных законов управления движением КЛА на основе уже известных естественных закономерностей — законов Кеплера, которые можно записать в виде следующих инвариантов — интегралов движения:
- первый закон — инвариант
$$
\omega_1=r(1+e\cos\theta)-p=0,\qquad
(3.47)$$ - второй закон — инвариант
$$
\omega_2=r^2\dot\theta(t)-h=0.\qquad
(3.48)$$
Перейдем к синтезу законов управления $U_r$ и $U_\theta$, опираясь на метод АКАР [61, 90].
Выберем в качестве инвариантных многообразий $\dot \omega_1(t)=0$ и $\omega_2=0$. При этом $\dot \omega_1(t)=0$ — это динамический инвариант, дополняющий инвариант Кеплера. В полярных координатах функции $\dot \omega_1(t)$ и $\omega_2$
с учетом инварианта $\omega_1$ (3.47) имеют вид
$$
\dot \omega_1(t)=p r^{-1}\dot r (t) - er\dot\theta(t)\sin\theta = p V_r r^{-1}-e V_\theta\sin\theta\qquad
(3.49)$$и
$$
\omega_2=r^2\dot\theta(t) -h =r V_\theta - h.\qquad
(3.50)$$
Сформируем теперь следующие инвариантные соотношения:
$$
\ddot\omega_1(t) + \Phi\dot \omega_1(t)=0\qquad
(3.51)$$
и
$$
\dot\omega_2(t) + \Phi \omega_2(t)=0.\qquad
(3.52)$$
Тогда, подставляя $\dot \omega_1(t)$ (3.49) и $\omega_2$ (3.50) в (3.51) и (3.52), в результате совместного решения находим следующие законы управления:
$$
U_r=\frac{h^2}{pr^2} -\frac{(\omega_2 +h)^2}{pr^2} - \frac{\Phi}{p}\big[r\dot\omega_1(t) + e\omega_2\sin\theta\big]\qquad
(3.53)$$
и
$$
U_\theta=-\frac{\omega_2}{r}\Phi.\qquad
(3.54)$$На пересечении инвариантных многообразий $\dot \omega_1(t)=\omega_2=0$ законы (3.53) и (3.54) “обнуляются” и, следовательно, КЛА будет устойчиво двигаться вдоль заданной орбиты — предельного цикла. Эти законы на пересечении инвариантных многообразий $\dot \omega_1(t)=0$ и $\omega_2=0$ редуцируются в известный закон всемирного тяготения Ньютона (3.46), если из выражения (3.53) исключить составляющую $\dfrac{h^2}{pr^2}$.
Выберем в (3.53) и (3.54) функцию $\Phi$ в форме
$$
\Phi=\frac{k \dot r(t)}{p}=\frac{k V_r}{p},\qquad
(3.55)$$
где $k$ — коэффициент интенсивности гравитационного поля, $k\LQ 1$.
В сильных гравитационных полях коэффициент $k$, по-видимому, зависит от величины гравитационного радиуса $\alpha$ “притягивающего” тела $M$ и его геометрического радиуса $r$, т.е.
$$
k=\frac{\alpha}{r}.\qquad
(3.56)$$
Разумеется, что соотношение (3.56) — это некоторое предположение.
Подставив теперь $\dot \omega_1(t)$ (3.49) и $\omega_2$ (3.50) в (3.53) и (3.54), выразим законы управления через скорости $V_r$ и $V_\theta$:
$$
U_r=\frac{h^2}{pr^2} -\frac{V_\theta^2}{p}-(V_rp -eh\sin\theta)\frac{kV_r}{p^2}\qquad
(3.57)$$
и
$$
U_\theta=-\left(V_\theta -\frac{h}{r}\right)\frac{kV_r}{p}.\qquad
(3.58)$$
Из (3.57) и (3.58) следует, что синергетическое упраление КЛА является тангенциальной (касательной) тягой, которая “исчезает” в момент выхода КЛА на заданную орбиту движения. Подчеркнем, что (3.57) и (3.58) — это естественные законы управления движением КЛА, выводящие систему (3.44), (3.45) на пересечение инвариантных многообразий $\omega_1=\dot \omega_1(t)=\omega_2=0$, на которых $U_r$ и $U_\theta$ “обнуляются”, и далее движение системы определяется законом тяготения Ньютона (3.46).
Отметим одну прикладную особенность функции $\Phi$ (3.55), входящей в законы (3.53), (3.54), (3.57) и (3.58). В теории тяготения естественно предполагается, что радиальная скорость имеет положительное направление, т.е. $\dot r(t)=V_r>0$. Однако при управлении КЛА, функционирующих, например, в атмосфере Земли, следует учитывать возможность, что в результате действия внешних возмущений скорость $V_r$ может изменить свое направление. Отсюда следует, что при решении практических задач управления КЛА целесообразно выбирать функцию $\Phi$ (3.55) как определенно-положительную, т.е.
$$
\Phi=\frac{k |V_r|}{p}.
$$
На практике в (3.57) и (3.58), по-видимому, целесообразно положить коэффициент интенсивности \mbox{$k=1$}, что также согласуется с энергетическими соображениями. Энергия системы изменяется во времени согласно следующим уравнениям [96]:
$$
\begin{split}
E(t) &=0,5\big(V_r^2 + V_\theta^2\big)-\frac{h^2}{pr};\\
\dot E(t) &= V_rU_r +V_\theta U_\theta.
\end{split}
$$
На основе законов управления $U_r$ (3.57) и $U_\theta$ (3.58) путем задания желаемых параметров $e=e_0<1$ и $p=p_0$ может быть осуществлено полное или частичное изменение элементов орбиты движения КЛА. При этом будет обеспечено достижение желаемых величин энергии $E_0=\dfrac{(e^2-1)h_0^2}{2p_0^2}<0$ и параметра $h_0=\sqrt{Gp_0}$. Полагая, в частности, $e_0=1$ и следовательно, $E_0=0$, мы получим решение задачи разгона КЛА до параболической скорости, а при $e_0>1$ и $E_0>0$ будет реализовано движение КЛА по желаемой гиперболической траектории и т.д.
Таким образом, на основе естественных закономерностей — инвариантов Кеплера (3.47) и (3.48), дополненных динамическим инвариантом $\dot \omega_1(t)=0$ (3.49), синтезированы системные законы управления (3.57) и (3.58), обеспечивающие устойчивое орбитальное движение КЛА. Эти законы “обнуляются” на инвариантных многообразиях $\dot \omega_1(t)=0$ (3.49) и $\omega_2=0$ (3.50), в результате чего КЛА будет двигаться по заданной орбите, определяемой его гравитационным взаимодействием с центральным телом, например, Землей.
Системные законы (3.57) и (3.58) структурно включают в себя закон тяготения Ньютона (3.46), который имеет наивысший приоритет в этой “асимптотической” цепи законов тяготения.
Итак, на основе метода АКАР [61, 90] аналитически построены объективные системные законы тяготения, основанные на естественных закономерностях гравитационного взаимодействия двух тел.
Подчеркнем, что с точки зрения принципа “расширения — сжатия” фазового пространства, лежащего в основе метода АКАР, законы управления (3.57) и (3.58) являются своего рода очередным этапом “асимптотической эстафеты”. В самом деле, эти законы можно толковать как внешнюю “матрешку”, “надетую” на закон тяготения Ньютона (3.46). На наш взгляд, выявленная здесь замечательная “эстафета” законов тяготения как раз и отражает идеологию единства процессов самоорганизации и самоуправления в теории гравитационного взаимодействия тел. Удивительно, что учет особенностей прикладной задачи (3.44), (3.45) привел к определенному обобщению исходной задачи тяготения. Подобное нередко случалось в истории науки.
Таким образом, начав рассмотрение прикладной задачи, мы фактически пришли к обобщенной в форме системных законов тяготения (3.57) и (3.58). В самом деле, исключив из (3.57) составляющую $\dfrac{h^2}{pr^2}$, мы получим обобщенные системные законы тяготения, структурно включающие в себя закон тяготения Ньютона (3.46). Дальнейшее обобщение лежит на пути учета процессов эволюции параметров $e$ и $p$ орбиты движения тел.
На практике законы (3.57) и (3.58) могут использоваться в качестве базовых при решении важных задач управления КЛА, навигации Земли с помощью спутниковых систем и др.
Для примера на рис. 3.8, рис. 3.9, рис. 3.10, рис. 3.11, рис. 3.12, рис. 3.13, рис. 3.14 приведены результаты моделирования системы управления КЛА с параметрами орбиты: $e=0$, $p=36000$ км, $T=24$ часа, $h=\dfrac{2\pi p^2}{T}$, $k=1$. В этом случае орбитой является окружность с радиусом $r=p$. Аналогично на рис. 3.15, рис. 3.16, рис. 3.17, рис. 3.18, рис. 3.19, рис. 3.20, рис. 3.21 приведены результаты моделирования системы управления КЛА с параметрами эллиптической орбиты: $e=0,5$, $p=36000$ км, $T=24$ часа, $a=\dfrac{p}{1-e^2}$, $b=\dfrac{p}{\sqrt{1-e^2}}$, $h=\dfrac{2\pi ab}{T}$, $k=1$. В отличие от предыдущего случая $r(t)$ и $\dot r(t)=V_r$ являются периодическими функциями времени.
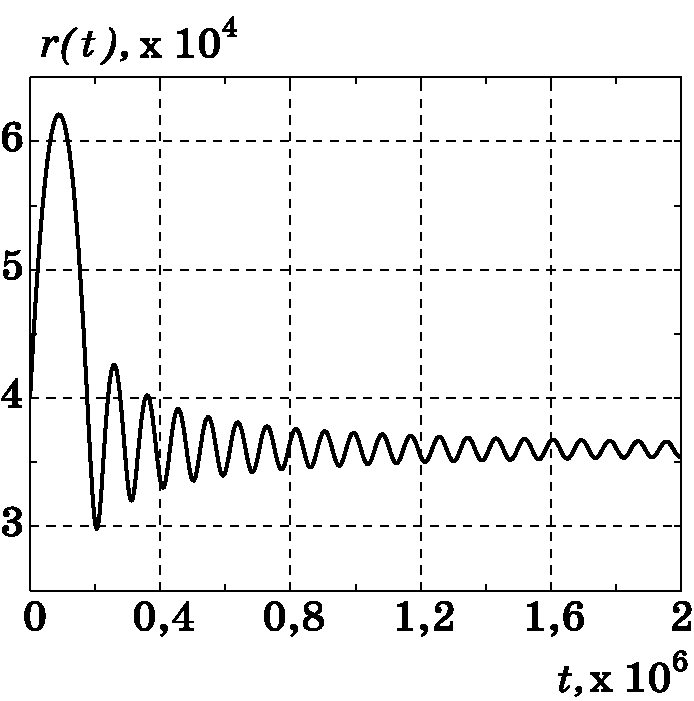
Рис. 3.8. График изменения $r(t)$
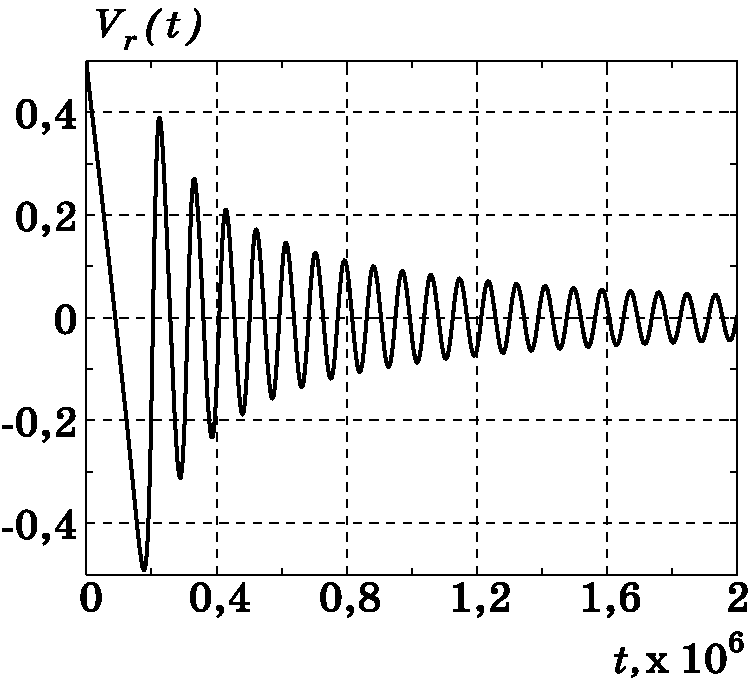
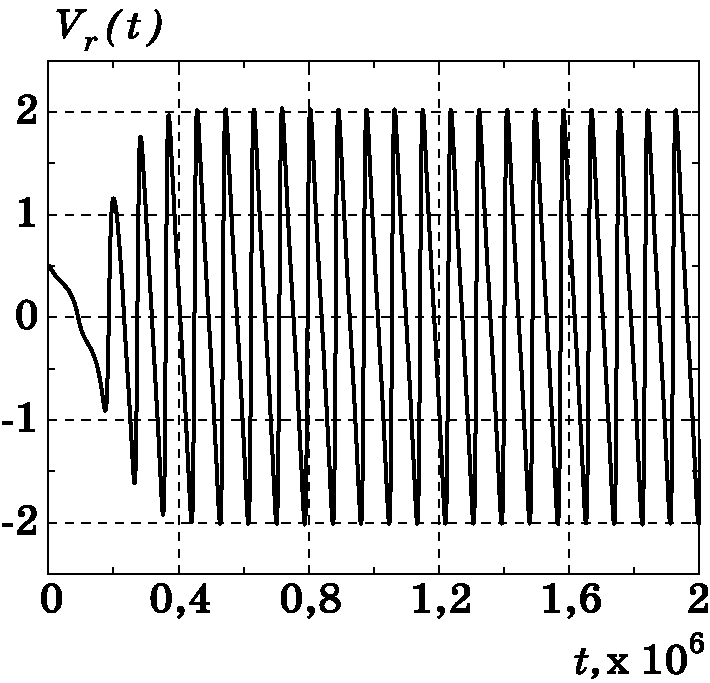
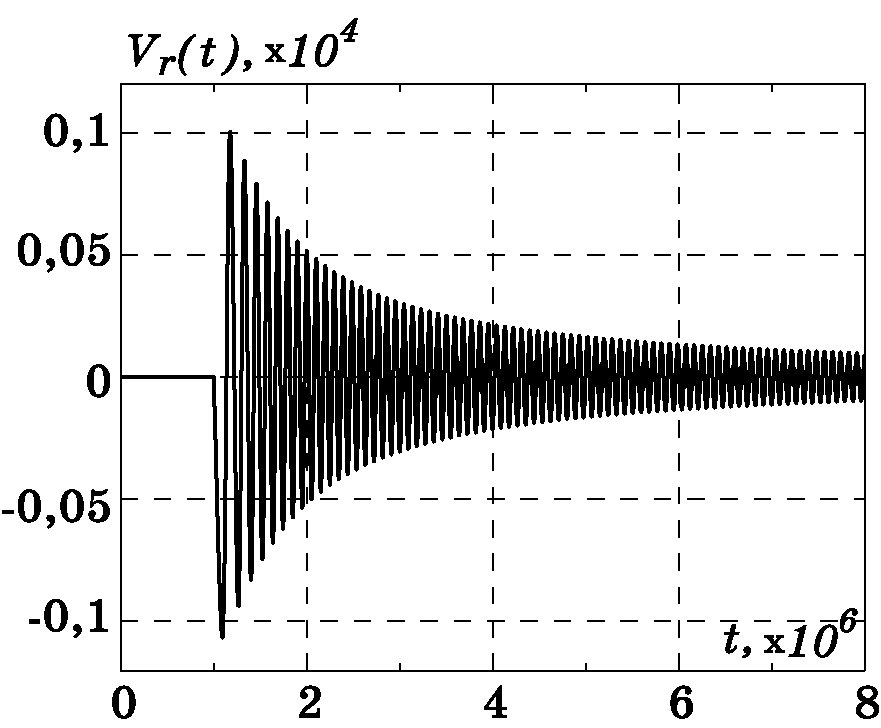
Рис. 3.9. График изменения $\dot {r}(t)=V_{r}(t)$
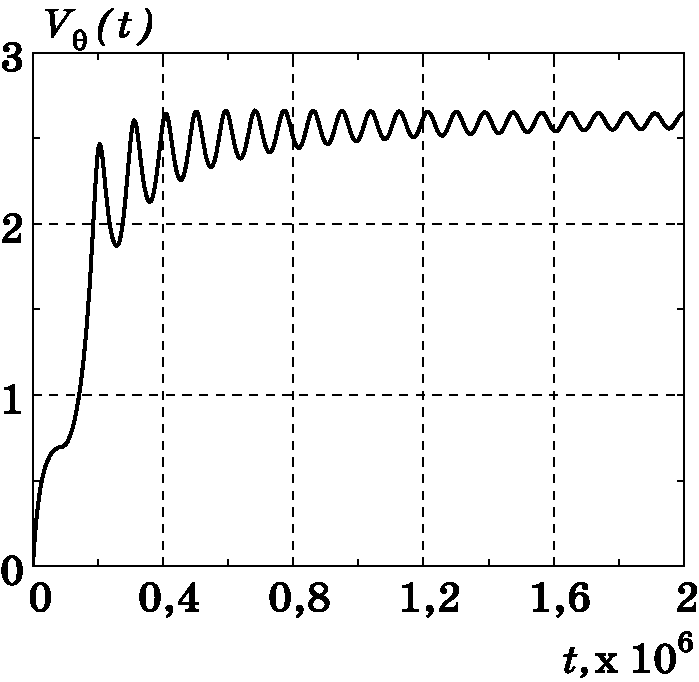
Рис. 3.10. График изменения $V_\theta(t)$
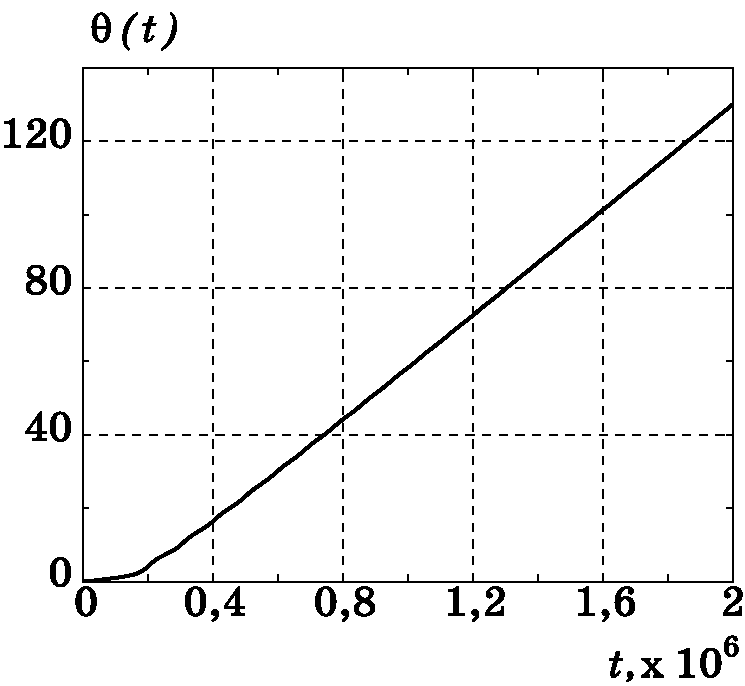
Рис. 3.11. График изменения $\theta(t)$
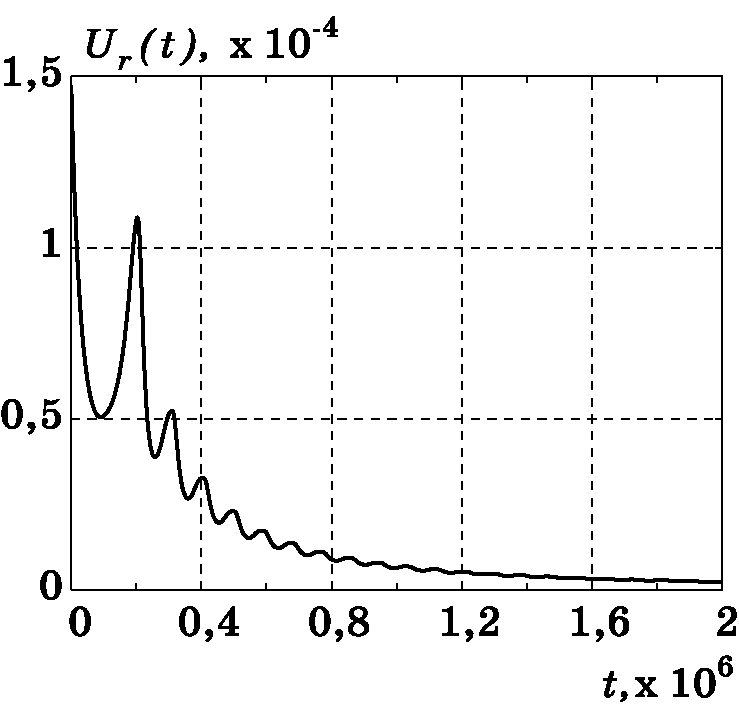
Рис. 3.13. График изменения $U_{r}(t)$
 %
%
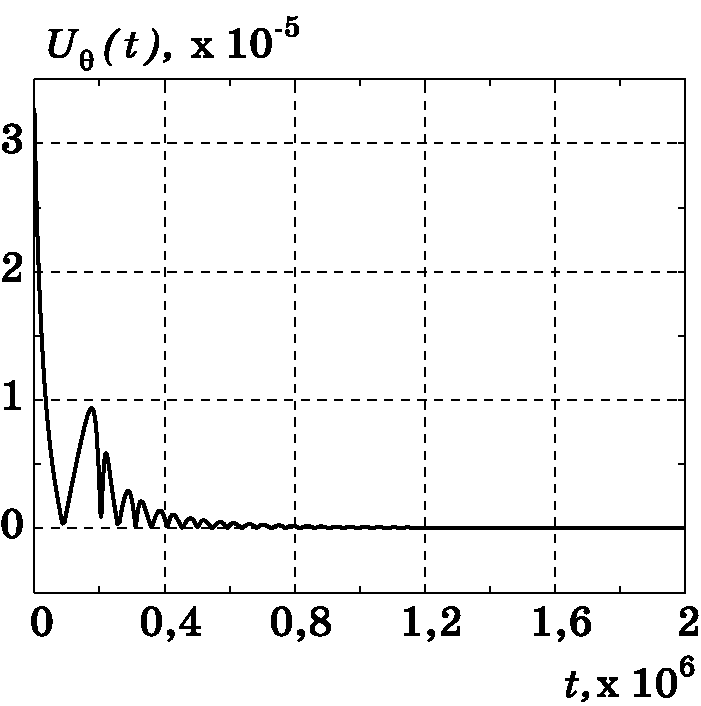
Рис. 3.14. График изменения $U_\theta(t)$
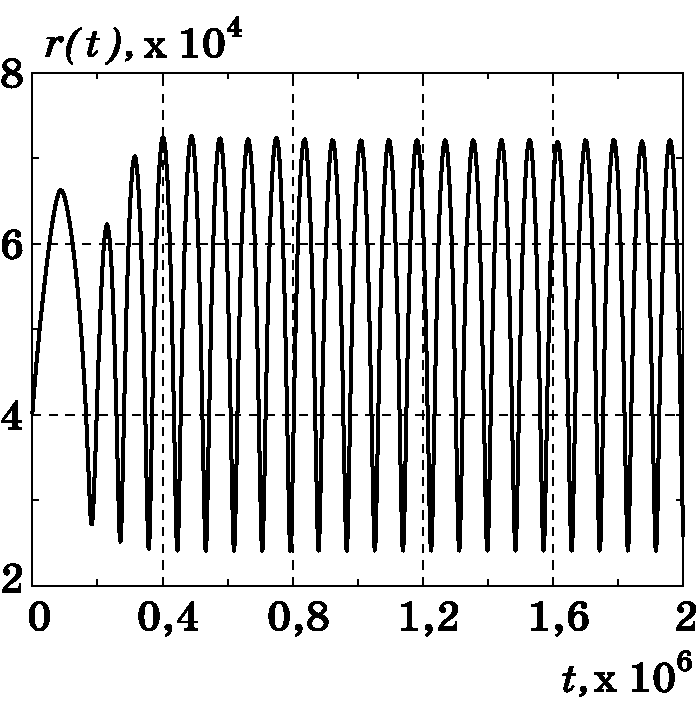
Рис. 3.15. График изменения $r(t)$
Рис. 3.16. График изменения $\dot {r}(t)=V_{r}(t)$
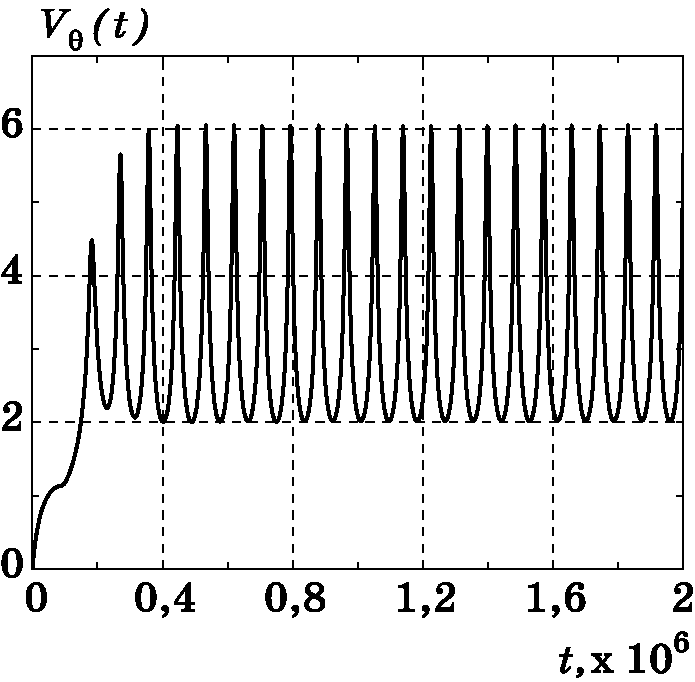
Рис. 3.17. График изменения $V_\theta(t)$
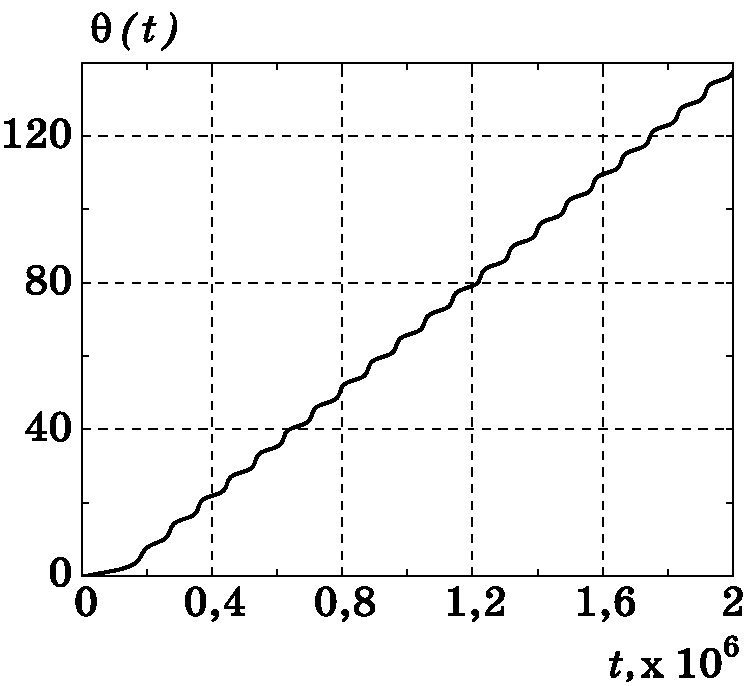
Рис. 3.18. График изменения $\theta(t)$
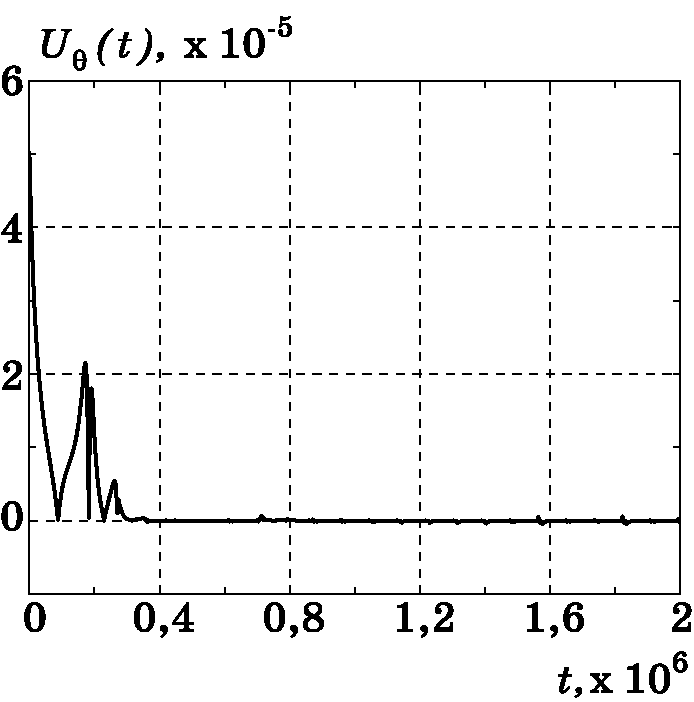
Рис. 3.20. График изменения $U_{r}(t)$
Рис. 3.21. График изменения $U_\theta(t)$
На рис. 3.22, рис. 3.23, рис. 3.24, рис. 3.25 представлены результаты моделирования системы управления КЛА при переходе его на новую орбиту: $p=36000$ км, $T=24$ часа из произвольных начальных условий. Для реализации такого перехода следует лишь задать желаемые параметры: $p$, $e$, $T$ и $h$ в законах управления (3.57) и (3.58) КЛА. Отметим, что в работе [97] предпринята попытка решения указанной задачи перевода КЛА на новую орбиту. При этом управление ищется в виде функции времени при строго заданных начальных условиях. Удивительно, что такой подход, мало приемлемый на практике, почему-то в [97] отнесен к “новому классу задач управления”. Синергетические же законы управления (3.57), (3.58) элегантно решают эту “сложную задачу” [97] для произвольных начальных условий движения КЛА.
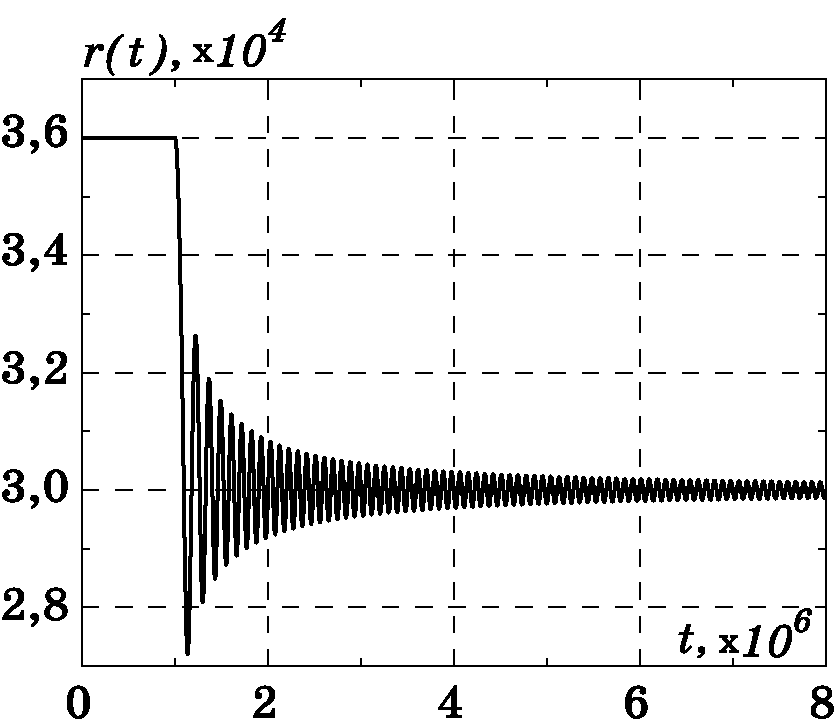
Рис. 3.22. График изменения $\theta(t)$
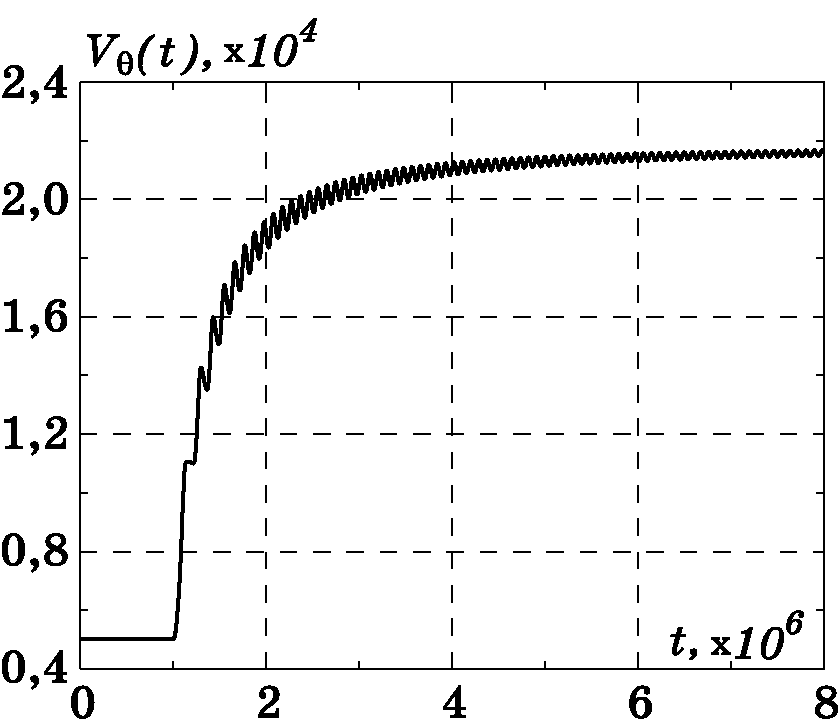
Рис. 3.24. График изменения $U_r(t)$
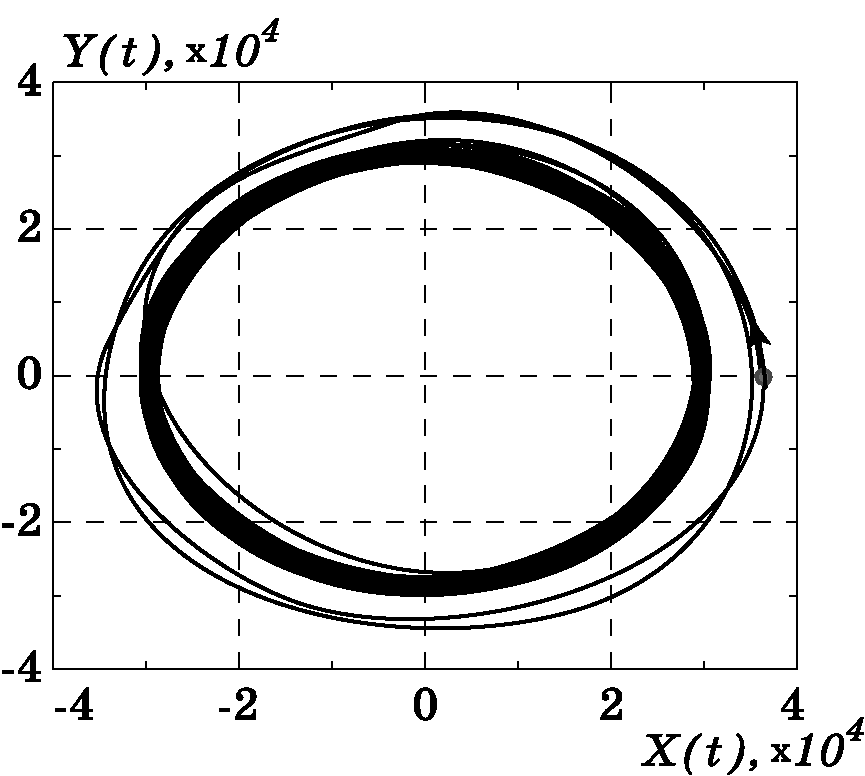
Рис. 3.25. График изменения $U_\theta(t)$
Приведенные результаты моделирования системы управления КЛА полностью подтверждают изложенные в разделе научные положения.
Учитывая универсальный характер системных законов тяготения (3.57), (3.58) выделим их основные отличительные особенности:
- первая особенность этих законов состоит в том, что он неизбежно переводят систему двух гравитационно взаимодействующих тел из произвольного начального состояния (в определенной физической области) на пересечение инвариантных многообразий $\omega_1=0$, $\dot\omega_1(t)=0$, $\omega_2=0$. Иначе говоря, законы (3.57), (3.58) обеспечивают асимптотическую устойчивость орбитального движения. Судя по многочисленной литературе, о такого рода устойчивости в теории тяготения речь обычно не идет. Напомним [98], что еще Лаплас, рассматривая орбитальные движения под действием закона тяготения Ньтона (3.46), доказал периодичность возмущений в экцентриситете эллиптических планетарных орбит. Он показал, что величины этих возмущений колеблются в определенных пределах, а не растут неограниченно, тем самым нарушая регулярность планетных движений. Как подчеркивается в [98], “смысл результата, полученного Лапласом, приближенно можно истолковать как утверждение об устойчивости Вселенной”. Согласно же синергетическим законам тяготения (3.57), (3.58) орбитальное движение двух взаимодействующих тел обладает важным свойством асимптотической устойчивости относительно инвариантных многообразий $\omega_1=\dot\omega_1(t)=\omega_2=0$, а это, несомненно, внушает исторический оптимизм…;
- вторая особенность системных законов (3.57), (3.58) состоит в том, что он, в отличие от закона Ньютона, является динамическим и содержит в себе скоростные составляющие $V_r$ и $V_\theta$. Эта особенность системных законов позволяет несколько ослабить ту жесткую критику, которой всегда подвергался закон Ньютона, фактически предполагавший физически сомнительную неограниченную скорость гравитационного взаимодействия тел. Необходимо подчеркнуть, что и сам великий Ньютон великолепно это понимал: “Предполагать, что тяготение является существенным, неразрывным и врожденным свойством материи, так что тело может действовать на другое на любом расстоянии в пустом пространстве, без посредства чего-либо передавая действие и силу, — это, по-моему, такой абсурд, который немыслим ни для кого, умеющего разбираться в философских предметах. Тяготение должно вызываться агентом, постоянно действующим по определенным законам. Является ли, однако, этот агент материальным или нематериальным, решать это я предоставил моим читателям” [99];
- третья особенность системных законов (3.57), (3.58), которая в мировоззренческом плане существенно отличает их от закона Ньютона, состоит в том, что они предполагают активность сил поля тяготения. Это отличие во многом согласуется с фундаментальной концепцией современного научного познания о самоорганизации сложных систем, к которым, несомненно, относятся системы гравитационного взаимодействия тел. Авторы работы [100] следующим образом изложили эту концепцию: “Стабильный ньютоновский мир плавных постепенных изменений, сотворенный однажды Богом и сохраняемый им в этом качестве посредством своего активного присутствия во всем — и в большом и в малом, — может быть представлен как результат процесса самоорганизации некоей непрерывной нелинейной среды, заполняющей всю Вселенную. В рамках этой картины материальные тела могут интерпретироваться как устойчивые локализованные процессы, ... ответственность за взаимодействие между которыми берут на себя в конечном счете уже не силы как таковые, а интегральные характеристики некоторой активной нелинейной среды. Таким образом, например, предложенная Ньютоном модель Солнечной системы может быть представлена как некоторая ассимптоматика процесса самоорганизации активной мировой субстанции, или среды, которая является носителем определенного класса структур, существующих в ней латентно, в виде спектра потенциально возможных динамических стабильных образований”.
Указанная концепция тяготения является синергетической и, на наш взгляд, весьма перспективной. Собственно говоря, наша работа конкретизирует и развивает именно эту философскую концепцию. В ее контексте синергетические законы тяготения (3.57), (3.58) являются системными и структурно-образующими, так как они, в отличие от закона Ньютона, формируют новые динамические структуры, которые, скрытно присущи гравитационному взаимодействию тел. Системные законы построены по схеме “асимптотической эстафеты”, согласно которой латентные структуры по мере асимптотически устойчивого движения системы к пересечению инвариантных многообразий $\dot\omega_1(t)=0$, $\omega_2=0$ постепенно “исчезают”. Это и свидетельствует о том, что системные законы (3.57), (3.58) реализуют концепцию единства процессов самоорганизации и самоуправления (взаимодействия), пронизывающую окружающую нас природу. Согласно этой концепции, системные законы (3.57), (3.58), “охватывающие” закон Ньютона как свою динамическую редукцию на инвариантных многообразиях $\dot\omega_1(t)=0$ и $\omega_2=0$, по-видимому, также может быть “поглощены” следующим более общим звеном “асимптотической эстафеты” законов тяготения. Иначе говоря, системные законы (3.57), (3.58), в свою очередь, может являться следующей редукцией на многообразиях более высокого уровня понимания сущности гравитационных явлений.
В работах [92, 93] приведены некоторые астрофизические следствия из системных законов тяготения (3.57), (3.58), позволивших объяснить ряд ранее непонятных явлений в небесной механике.
Подведем некоторые итоги рассмотрения синергетической гипотезы тяготения. Впервые предложенный в работах [92, 93] синергетический подход к синтезу системных законов тяготения, основанный на концепции единства процессов самоорганизации и управления, позволяет, опираясь на базовые естественные закономерности, построить системную теорию притягивающих взаимодействий, лежащих, как известно, в основе т.н. “законов природы”. В разделе показано, что системные “законы природы”, имеющие динамическую природу, могут быть построены на основе концепции “асимптотической эстафеты” моделей движения систем, или, иначе говоря, путем “одевания” на известные закономерности следующей, более общей, “матрешки”, затем следующей и т.д.
Для демонстрации эффективности и перспективности указанной концепции целесообразно было рассмотреть примеры неординарных и даже экзотических задач, издавна находящихся в сфере повышенного внимания ученых. Так, например, небесная механика и классическая наука сделали принципиальный рывок в своем развитии в результате успешного продвижения в понимании устройства мира согласно концептуальной схеме моделей: “Коперник $\to$ Кеплер $\to$ Ньютон!” На основе гелиоцентрической идеи Коперника и обработки многочисленных наблюдений движения планет, выполненных Тихо Браге, Иоганом Кеплером были выявлены знаменитые законы (инварианты) движения двух гравитационно взаимодействующих тел “звезда — планета”. Затем Ньютоном был построен закон тяготения, объяснивший законы Кеплера, и в результате были сформулированы не только концептуальные основы небесной и затем классической механики, но и указаны базовые направления их развития. Согласно этим основам, три закона Кеплера являются следствием закона тяготения Ньютона, что в совокупности и образует фундамент гелиоцентрической системы планетного движения Коперника.
Однако, несмотря на эти величайшие достижения, многие ключевые вопросы о причинах и законах движения планет и тел во Вселенной остаются до сих пор открытыми. За последние 300 лет эти вопросы тревожили многих выдающихся ученых и, следовательно, являлись источником развития науки. Так, например, возникает вопрос: если движение тел строго подчиняется закону тяготения Ньютона и это движение устойчиво относительно инвариантов Кеплера, то каковы все же истинные законы взаимодействия тел при произвольных начальных условиях? Иначе говоря, каковы законы гравитационного взаимодействия, из которых, как редукция, следует известный закон тяготения. Или, по другому, закон тяготения Ньютона — это конечный “продукт” концептуальной схемы “Коперник $\to$ Кеплер $\to$ Ньютон” или же в природе существуют более общие, “скрытые” (латентные) системные закономерности гравитационного взаимодействия тел? На наш взгляд, ответы на эти фундаментальные вопросы лежат в русле схемы: “системные законы гравитационного взаимодействия $\to$ инварианты Кеплера $\to$ закон тяготения Ньютона $\to$ движение по коническим сечениям”.
Предполагая оправданной такую постановку задачи взаимодействия тел, которая, возможно, может быть даже интерпретирована как своего рода “покушение на основы” теории тяготения, можно, оказывается, дать вполне положительный ответ и построить системные законы гравитационного взаимодействия, которые в нашей терминологии относятся к классу законов единства процессов самоорганизации и самоуправления [90].
Выше построены такого рода системные законы (3.57), (3.58) притягивающего взаимодействия двух тел, которые сначала переходят друг в друга, а затем на гравитационных инвариантах превращаются в известный закон тяготения Ньютона. Сам же закон Ньютона в этом “асимптотическом” ряду занимает ключевое положение, являясь опорным ядром последующих системных законов тяготения, имеющих латентный характер.
Это, вообще говоря, удивительный результат, из которого, между прочим, следует важный вывод: известные законы тяготения и, по-видимому, все законы классической механики — это т.н. законы “консервативной самоорганизации” [101], описывающие взаимодействие тел в условиях динамического равновесия между притоком и диссипацией энергии.
Аналогичные системные законы взаимодействия можно построить и в других областях естествознания и техники [90, 102—105].
Что же касается возможного якобы “покушения на основы” теории тяготения, то здесь, в оправдание предпринятого автором выдвижения синергетической гипотезы, вполне уместно привести следующие замечательные высказывания, разделенные промежутком времени в 400 лет.
Во “Введении для читателя” к ныне знаменитой, а тогда крамольной и преследуемой инквизицией, книге Коперника “Об обращении небесных тел” лютеранский богослов Осиандер в 1543 г. писал: “Задача астронома заключается в том, чтобы путем искусственных и тщательных наблюдений собрать воедино историю небесных движений, а затем — поскольку он не в состоянии никакими умозаключениями дойти до истинных причин этих движений — придумать или сконструировать какую-либо причину или гипотезу по своему разумению, чтобы на ее основе вычислить из геометрических принципов движения светил как в прошлом, так и в будущем... Если [математическая астрономия] и изобретает причины— а для этого, конечно, приходится много и напряженно думать, — то она тем не менее делает это не для того, чтобы убедить кого-либо в их истинности, а для того, чтобы создать подходящую основу для вычислений. А пока гипотезы преходящи, не будем ожидать чего-либо несомненного от астрономии, ибо астрономия не может предложить нам ничего определенного” [цит. по 106].
Это “Введение” сурово осуждали Кеплер и Галилей, которые называли его “лукавым”, а Джордано Бруно называл Оссиандера “ослом”. Однако имеются правдоподобные соображения, что Оссиандер как раз и пытался спасти книгу Коперника. Похоже, что именно его “Введение” усыпило бдительность тогдашней инквизиции, а книга Коперника была опубликована и распространялась более 70 лет вплоть до ее окончательного запрещения [107]. Эта великая книга оказала непреходящее влияние на развитие всего естествознания.
Второе высказывание принадлежит Р. Фейнману: “Если Вам удастся придумать точку зрения на мир, которая согласуется со всем тем, что уже выяснено и приводит где-то к другим результатам в сомнительных областях, Вы делаете великое открытие. Найти же теорию, которая согласуется с экспериментом, где справедливость существующих теорий уже установлена и в то же время приводит в других областях к каким-то новым выводам, даже если они не согласуются с результатами эксперимента почти невозможно. Но только почти. Новые идеи придумывать очень трудно. Для этого требуется совершенно исключительное воображение” [108].
И, наконец, процитируем высказывание, принадлежащее известному астроному XX века Р. Дикке,: “...всякая серьезная теория тяготения в предельном случае достаточно слабых полей или достаточно малых скоростей движения тел, связанных гравитационным взаимодействием, должна переходить в ньютоновскую теорию тяготения” [109]. Такой переход, разумеется, присущ и синергетической гипотезе тяготения.
Процитированные здесь замечательные высказывания незаурядных людей говорят о многом. Изложенные в них яркие мысли стали для автора своего рода стимулом для выдвижения новой синергетической гипотезы тяготения, которая отражает его личную точку зрения на одну из самых загадочных тайн науки.