Модуль 2. Общий метод аналитического конструирования нелинейных агрегированных регуляторов

2.7. Аналитическое конструирование нелинейных агрегированных регуляторов с ограничением координат и управления

Для многих современных систем управления различными объектами в механике, робототехнике, энергетике и т.д. выдвигается основное требование — интенсификация технологических процессов. Это приводит к необходимости постановки и решения ряда новых задач управления, в частности требует обязательного рассмотрения нелинейных математических моделей движения управляемых объектов. Другой особенностью таких задач, связанной с напряженностью режимов работы оборудования, является учет ограничений, накладываемых на допустимые диапазоны изменения фазовых координат. Эти ограничения определяются заданным технологическим регламентом протекания тех или иных процессов, когда тепловые нагрузки, механические напряжения, скорости протекания веществ и т.п. приближаются к предельно допустимым значениям. Учет ограничений в процессе синтеза систем управления позволяет выполнить требования, характеризующие качество продукции, и повысить надежность работы технологических установок.

Необходимо отметить, что решение задачи синтеза оптимальных законов управления с учетом ограничений, как правило, усложняется. Так, в работе [69] указывается, что решение задачи АКОР с учетом ограничений, основанное на использовании квадратичных функционалов Летова—Калмана, приводит к неаддитивным управлениям в том смысле, что в синтезируемых законах трудно выделить часть, обеспечивающую собственно оптимальное управление, и часть, отвечающую за выполнение заданных ограничений. В методе же АКОР по критерию обобщенной работы [64, 69] вследствие линейности функционального уравнения обеспечивается аддитивность управлений, что и позволяет синтезировать так называемые автоматы ограничений. В работе [69] приведены примеры синтеза таких автоматов применительно, в основном, к линейным объектам. Следует также отметить, что в работе [70] изложен метод синтеза оптимального по быстродействию управления линейными объектами с учетом ограничений фазовых координат.

Рассмотрим аналитическое конструирование систем управления нелинейными объектами при наличии ограничений на координаты и управление с использованием соответствующих агрегированных макропеременных. Отличительной чертой излагаемого подхода является простота и аналитичность выполняемых процедур синтеза законов управления [57, 150].

2.7.1. Ограничения на координаты и управления в форме неравенств

Перейдем сначала к рассмотрению задачи АКАР с учетом ограничений в виде неравенств на управление и координаты, т.е. $|u(t)|\le u_{\max}$ и $|x_i|\le x_{i\max}$. Учет таких ограничений представляет собой весьма сложную и далеко еще нерешенную задачу как в теории АКОР, так и вообще в любых других методах синтеза систем управления. Это связано с тем, что указанные ограничения на управления и координаты приводят к существенной нелинейности синтезируемого закона управления, тем более что задача усложняется для нелинейных объектов.

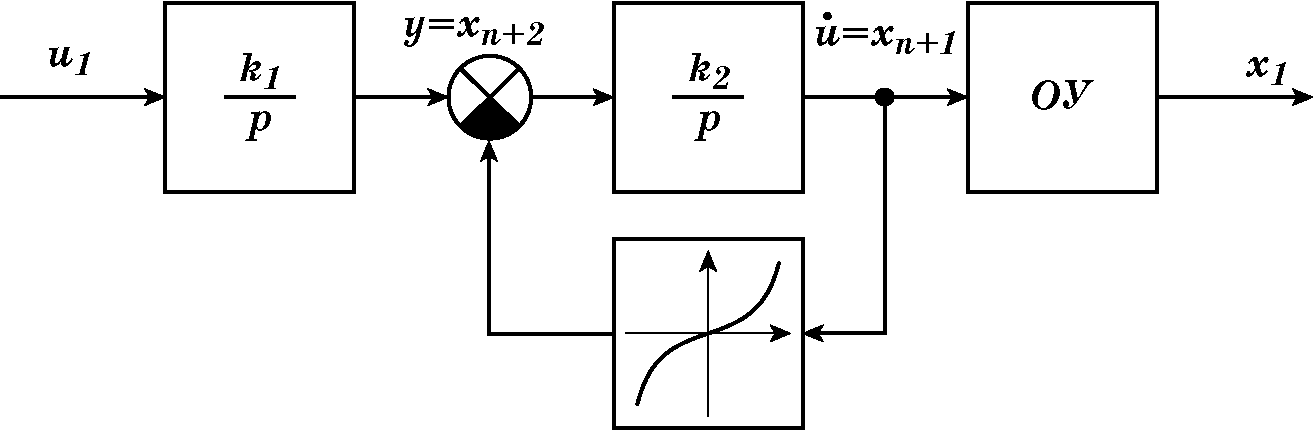
Рассмотрим задачу АКАР с учетом ограничения на управление. Можно предложить несколько способов учета этого ограничения. Одним из очевидных способов учета ограничения $|u(t)|\le u_{\max}$ является введение в канал управления статического звена, имеющего характеристику типа “насыщение”, т.е. обладающего свойствами релейного элемента в режиме больших отклонений. Отличительной особенностью такого способа является необходимость установки на выходе этого звена некоторого дополнительного динамического звена, например интегратора. Тогда за новое условное (неограниченное) управление следует выбрать управление $u_i$ на входе введенного интегратора. Следовательно, размерность неизменяемой части синтезируемой системы увеличивается на единицу по сравнению с размерностью сходного объекта.

Рис. 2.21. Структурная схема

На рис. 2.21 изображена структурная схема, отражающая предложенный способ учета ограничения на управление. Зависимость между действительным управлением $u$ и выходом введенного интегратора может быть выражена различными функциями с насыщением, например, вида
$$
u=\arctg by \quad \text{или} \quad u=A\tanh by.\qquad
(2.87)$$Тогда уравнения таким образом сформированной неизменяемой части можно записать, в частности, в форме
$$
\begin{split}
\dot x_j(t)&=f_j(x_1,\dots,x_j) +a_{j+1}x_{j+1}, \quad j=1,2,\dots,n-1;\\
\dot x_n(t)&=f_n(x_1,\dots,x_n)+u;\\
\dot y(t)&=\dot x_{n+1}(t)=u_1,
\end{split}\qquad
(2.88)$$где $x_1,\dots,x_n$ — координаты состояния исходного объекта; $u$ — исходное управление; $y=x_{n+1}$ — выходная координата дополнительного динамического звена; $u_1$ — условное управление.

С учетом (2.87) уравнения (2.88) приводятся к форме
$$
\begin{split}
\dot x_j(t)&=f_j(x_1,\dots,x_j) +a_{j+1}x_{j+1}, \quad j=1,2,\dots,n-1;\\
\dot x_n(t)&=f_n(x_1,\dots,x_n)+A\arctg bx_{n+1};\\
\dot x_{n+1}(t)&=u_1,
\end{split}\qquad
(2.89)$$Применительно к расширенному объекту (2.89) можно использовать процедуру АКАР на основе введения последовательной совокупности притягивающих многообразий понижающейся размерности. Для этого выбираем первую агрегированную макропеременную, например, в виде
$$
\psi_1=A\arctg x_{n+1} +u_2(x_1,\dots,x_n)\qquad
(2.90)$$и синтезируем управление $u_1(x_1,\dots,x_n)$, используя функциональное уравнение
$$
T_1\dot\psi_1(t) +\psi_1=0.\qquad
(2.91)$$Тогда, подставив $\psi_1$ (2.90) в (2.91), находим уравнение
$$
\frac{Ab\dot x_{n+1}(t)}{1+b^2x^2_{n+1}} +\sum_{k=1}^n\frac{\partial u_2(x_1,\dots,x_n)}{\partial x_k}\dot x_k(t) +\frac A{T_1} \arctg bx_{n+1} +\frac 1{T_1}u_2(x_1,\dots,x_n)=0.\qquad
(2.92)$$С учетом уравнений расширенного объекта (2.89) из (2.92) находим управление
$$
u_1{=}&-\frac{1{+}b^2x^2_{n+1}}{Ab}\Bigg\{\sum_{j=1}^{n-1}\frac{\partial u_2}{\partial x_j}\big[f_j(x_1,\dots,x_j) {+}a_{j+1}x_{j+1}\big] {+}\frac A{T_1}\arctg bx_{n+1} {+}\\
&{+}\frac{\partial u_2}{\partial x_n}\big[f_n(x_1,\dots,x_n) {+}A\arctg bx_{n+1}\big]{+}\frac 1{T_1} u_2(x_1,\dots,x_n)\vphantom{\sum_{j=1}^{n-1}\frac{\partial u_2}{\partial x_j} }\Bigg\}.\qquad
(2.93)$$Управление $u_1$ (2.93) переводит изображающую точку в окрестность многообразия $\psi_1=0$ (2.90), движение вдоль которого описывается следующей системой дифференциальных уравнений:
$$
\begin{split}
\dot x_j(t)&=f_j(x_1,\dots,x_j) +a_{j+1}x_{j+1}, \quad j=1,2,\dots,n-1;\\
\dot x_n(t)&=f_n(x_1,\dots,x_n)-u_2;\\
\end{split}\qquad
(2.94)$$К системе (2.94), имеющей размерность $n$, можно снова применить метод АКАР синтеза путем введения второй, третьей и т.д. вплоть до $m=n-1$ макропеременной понижающейся размерности:
$$
\begin{split}
\psi_2&=x_n+u_3(x_1,\dots,x_{n-1});\\
\psi_3&=x_{n-1} +u_4(x_1,\dots,x_{n-r}),\dots,;\\
\psi_m&=x_r +u_{m+1}(x_1).
\end{split}
$$Используя уравнения вида (2.91), определяем промежуточные управления $u_2, u_3,\dots,u_{n+1}$, а затем и управление $u_1$ (2.93). В соответствии с рис. 2.21 управление $u=\arctg bx_{n+1}$, действующее на исходный объект, будет ограничено $|u(t)|<A$ т.е. будет решена поставленная задача АКАР с учетом ограничения на управление.

Пример 1

Для иллюстрации предложенного способа учета ограничений на управление рассмотрим и исследуем задачу АКАР для следующего простого объекта:
$$
\dot x_1(t)=x_2; \quad \dot x_2(t)=u=A\arctg bx_3; \quad \dot x_3(t)=u_1.\qquad
(2.95)$$Введем сначала первую макропеременную вида (2.90)
$$
\psi_1=A\arctg bx_3 +u_2(x_1,x_2).\qquad
(2.96)$$Тогда, в соответствии с (2.94), для объекта (2.95) находим управление
$$
u_1=-\frac{1+b^2x_3^2}{Ab}\left[\frac{\partial u_2}{\partial x_1}x_2 +A\left(\frac{\partial u_2}{\partial x_{2}}+\frac 1{T_1}\right)\arctg bx_3 +\frac 1{T_1}u_2(x_1,x_2)\right].\qquad
(2.97)$$Управление (2.97) переводит изображающую точку в окрестность многообразия $\psi_1=0$ (2.96), движение вдоль которого описывается дифференциальными уравнениями
$$
\dot x_{1\psi_1}(t) =x_{2\psi_1}, \quad \dot x_{2\psi_1}(t) =-u_2(x_{1\psi_1},x_{2\psi_1}).\qquad
(2.98)$$Промежуточное управление $u_2$ найдем из уравнения
$$
T_2\dot \psi_2(t) +\psi_2=0
$$путем введения второй макропеременной
$$
\psi_2=\alpha_1x_1+x_2.
$$Используя $\psi_2$, с учетом (2.98) находим управление
$$
u_2=\frac{\alpha_1}{T_2}x_1 +\left(\alpha_1 +\frac 1{T_2}\right)x_2,\qquad
(2.99)$$которое переводит изображающую точку на многообразие $\psi_2=0$. Движение вдоль $\psi_2=0$ описывается уравнением
$$
\dot x_{1\psi_2}(t) =-\alpha_1x_{1\psi_2}.\qquad
(2.100)$$Условие устойчивости решения уравнения (2.100) весьма простое: $\alpha_1>0$. Подставив $u_2$ (2.99) в (2.97), находим закон управления
$$
u_1=-\frac{1+b^2x_3^2}{Ab}\left[\frac{\alpha_1}{T_1T_2}x_1 +\left(\frac{\alpha_1}{T_1} +\frac{\alpha_1}{T_2} +\frac 1{T_1T_2}\right)x_2 +A\left(\alpha_1 +\frac 1{T_1} +\frac 1{T_2}\right)\arctg bx_3\right].\qquad
(2.101)$$

Выбрав в (2.101) величины $T_1=T_2=\dfrac 1{\alpha_1}=T$ получаем
$$
u_1=-\frac{1+b^2x_3^2}{Ab}\left(\frac{x_1}{T^3} +\frac{3x_2}{T^2} +\frac{3A}{T}\arctg bx_3\right).\qquad
(2.102)$$На ЭВМ для разных начальных условий и параметра $T$ выполнено моделирование системы (2.95) с управлением $u_1$ (2.102). В рассматриваемом случае можно определить приближенную оценку времени затухания переходных процессов в замкнутой системе:
$$
t_p\le(3\dots 4)\left(T_1 +T_2 +\frac 1{\alpha_1}\right)\approx 10T.\qquad
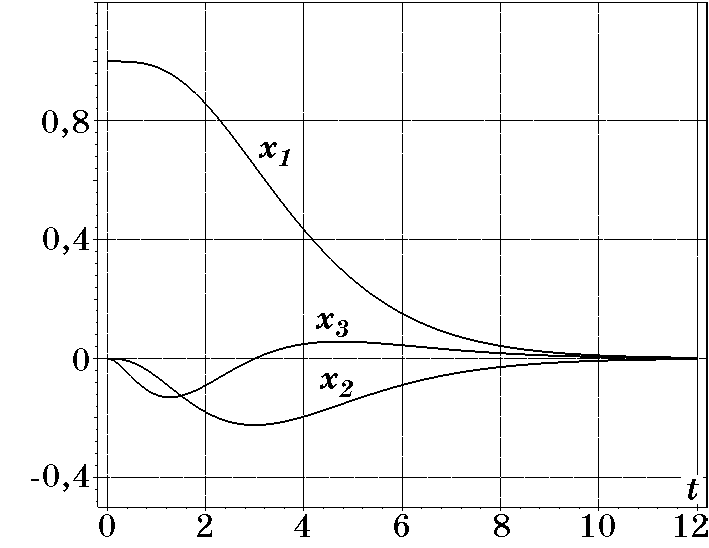
(2.103)$$На рис. 2.22 изображены графики переходных процессов для параметров $A=0,6366$; $b=20$; $T=0,5$ и $x_{10}=1$; $x_{20}=x_{30}=0$. В этом случае на переменную $u=A\arctg bx_3$ наложено ограничение $|u(t)|\le A\dfrac{\pi}2 =1$. Из рис. 2.22 видно, что переходные процессы по основным координатам $x_1(t)$, $x_2(t)$ объекта (2.95) имеют апериодический характер, выполняется ограничение ($u(t)_{\max}=-0,86$) на управление $|u|\le 1$ время регулирования $t_p\approx 4<5$, т.е. выполняется оценка (2.103).

На рис. 2.23 представлены переходные процессы при тех же начальных условиях, но при выборе $T=1$. В этом случае переходные процессы по $x_1(t)$ и $x_2(t)$ также являются апериодическими, время регулирования $t_p<10$ удовлетворяет оценке (2.103), а ограничение на $u$ существенно ослабляется ($u(t)_{\max}=-0,23$).

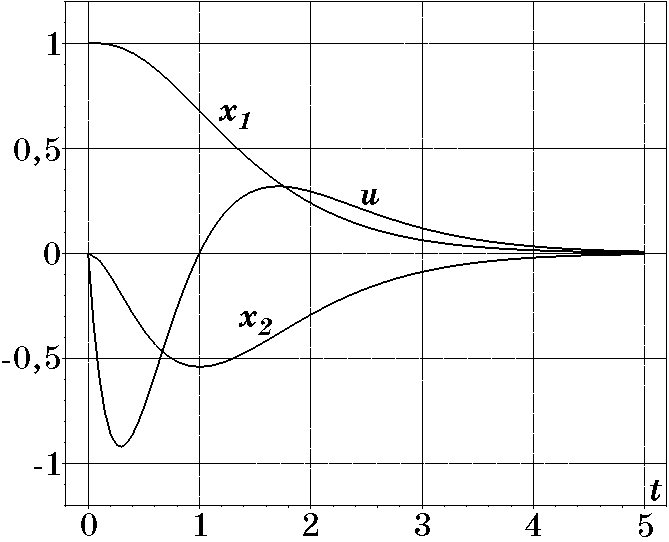
Рис. 2.22. Переходные процессы при $T=0,5$

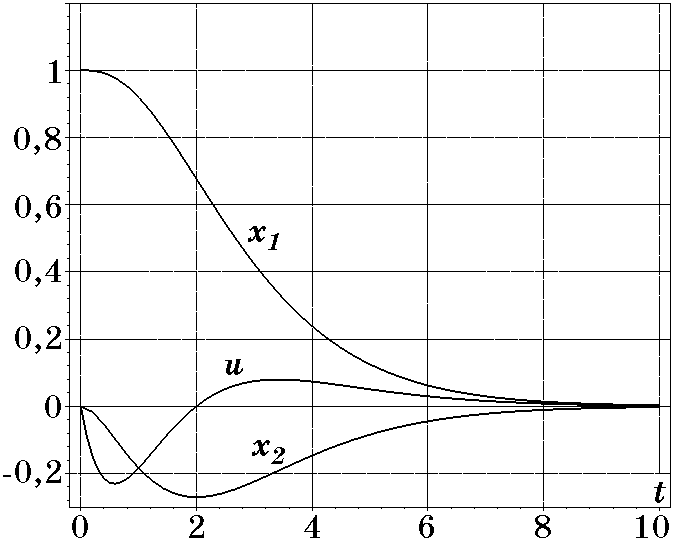
Рис. 2.23. Переходные процессы при $T=1$

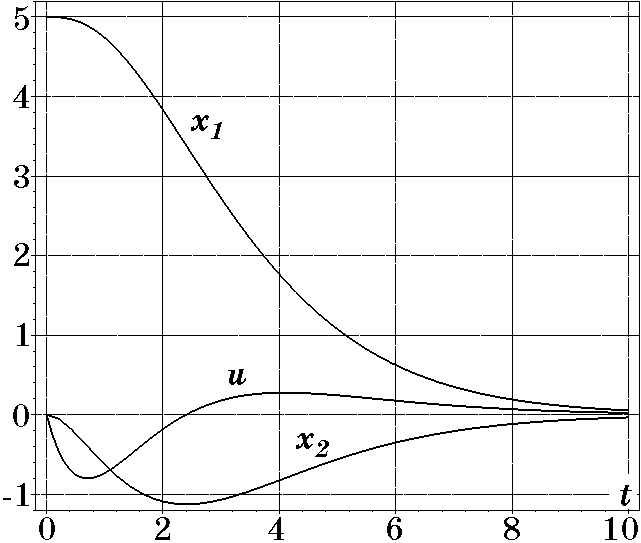
Рис. 2.24. Переходные процессы при $T=1,2$

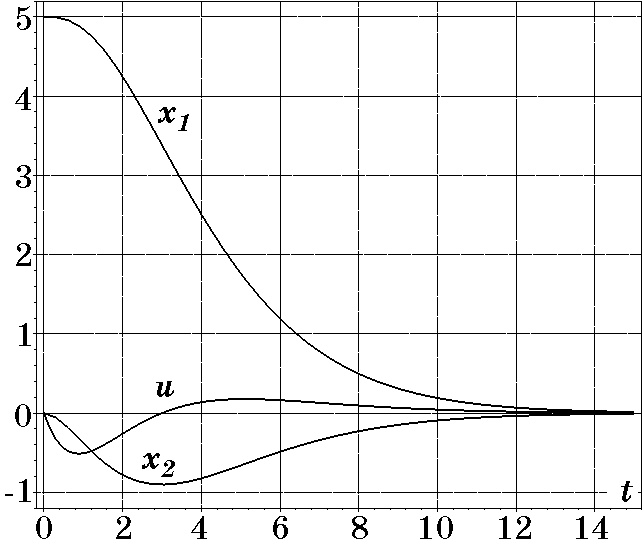
Рис. 2.25. Переходные процессы при $T=1,5$

Аналогично были исследованы переходные процессы в системе (2.95) для режима больших отклонений $x_{10}=5$; $x_{20}=x_{30}=0$ для разных $T$ и $u<1$. На рис. 2.24 изображены переходные процессы при $T=1,2$, которые имеют апериодический характер по координатам $x_1(t)$ и $x_2(t)$, время их затухания ($t_p\approx 9$) удовлетворяет оценке (2.103), а управление ($u(t)_{\max}=-0,8$) не превосходит заданного ограничения $|u|<1$. На рис. 2.25 представлены переходные процессы при тех же начальных условиях (\mbox{$x_{10}=5$;} $x_{20}=x_{30}=0$), но при $T=1,5$. Как видно из рис. 2.25, характер переходных процессов остается прежним, время их затухания ($t_p\approx 11$) удовлетворяет оценке (2.103), а ограничение на управление стало менее
жестким ($u(t)_{\max}=-0,51$). Еще более ослабляется
ограничение на управление (\mbox{$u(t)_{\max}=-0,28$)} при $T=2$, переходные процессы для которого изображены на рис. 2.26. При этом их характеристики остаются прежними. Таким образом, параметр $T$ в законе управления (2.102) оказывает существенное влияние как на время затухания переходных процессов в системе, так и на условия достижения ограничения на управление.

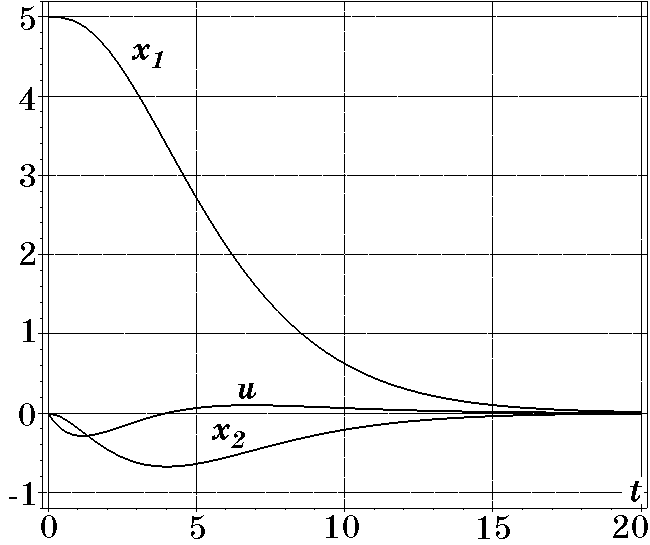
Рис. 2.26. Переходные процессы при $T=2$

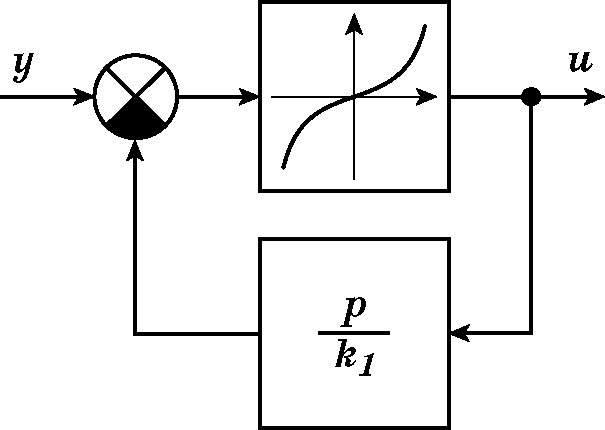
Перейдем далее к рассмотрению способа учета ограничений на управления и промежуточные координаты путем введения в цепи обратных связей динамических звеньев специальных обратных связей, имеющих резко возрастающие характеристики и зону нечувствительности в окрестности начала координат. Такого рода обратные связи давно используются в электроприводе в виде “отсечек” по скорости и току. На рис. 2.27 представлена структурная схема указанного способа введения обратных связей для учета ограничения на управление $|u|\le u_{\max}$.

Рис. 2.27. Структурная схема

Рассмотрим связь между переменными $y(t)$ и $u(t)$, записав уравнение
$$
\dot u(t)=k_1y -k_1\phi(u).\qquad
(2.104)$$Выбрав функцию $\phi(u)=A_1\tg b_1u$, из уравнения (2.104) получим
$$
u=\frac 1{b_1}\arctg\left(\frac 1{A_1}y -\frac 1{k_1A_1}\dot u(t)\right).\qquad
(2.105)$$

Рис. 2.28. Структурная схема

В соответствии с уравнением (2.105) можно построить структурную схему (рис. 2.28), из которой следует, что управление $u$ действительно будет ограничено некоторой величиной $u_{\max}=\dfrac{\pi}{2b_1}$, т.е. при $b_1=\dfrac{\pi}2$ имеем $|u|<1$. Итак, введение в цепь обратной связи интегратора звена с характеристикой вида $A_1\tg b_{1u}$ ограничивает его выход, т.е. управление $u$, действующее на объект. Запишем дифференциальные уравнения неизменяемой части, имеющей изображенную на рис. 2.27 структурную схему

\begin{split}
\dot x_j(t)&=f_j(x_1,\dots,x_j) +a_{j+1}x_{j+1}, \quad j=1,2,\dots,n-1;\\
\dot x_n(t)&=f_n(x_1,\dots,x_n)+u;\\
\dot u(t)&=k_1y -k_1A_1\tg b_1u;\\
\dot y(t)&=k_2u_1,
\end{split}\qquad
(2.106)$$где $x_1,\dots,x_n$ — координаты состояния исходного объекта; $u$ — исходное управление; $y$ — выходная координата второго дополнительного звена; $u_1$ — условное управление. Обозначив $u=x_{n+1}$, $y=x_{n+2}$, представим (2.106) в следующем виде:
$$
\begin{split}
\dot x_j(t)&=f_j(x_1,\dots,x_j) +a_{j+1}x_{j+1}, \quad j=1,2,\dots,n-1;\\
\dot x_n(t)&=f_n(x_1,\dots,x_n)+x_{n+1};\\
\dot x_{n+1}&=k_1x_{n+2} -k_1A_1\tg b_1x_{n+1};\\
\dot x_{n+2}&=k_2u_1.
\end{split}\qquad
(2.107)$$Для полученного расширенного объекта (2.107) можно использовать метод АКАР. Для этого введем сначала первую макропеременную $\psi_1=x_{n+2}+u_2(x_1,\dots,x_{n-1})$, затем вторую $\psi_2=x_{n+1}+u_3(x_1,\dots,x_{n})$, третью $\psi_3=x_{n}+u_4(x_1,\dots,x_{n-1})$ и т.д., вплоть до \mbox{$\psi_m=x_{2}+u_{m+1}(x_1)$}. Как было показано ранее, при этом можно обеспечить асимптотическую устойчивость в целом по координатам $x_1,x_2,\dots,x_n$, оценить время затухания переходных процессов и придать им желаемый (апериодический) характер. В [61] были приведены все необходимые выражения для синтеза управления $u_1(x_1,\dots,x_{n+2})$, основанные на последовательном использовании уравнений
$$
T_k\dot\psi_k(t) +\psi_k=0; \quad k=1,2,\dots,m<n-1.\qquad
(2.108)$$

Пример 2

Для примера синтезируем управление объектом вида (2.107), описываемым следующими дифференциальными уравнениями:
$$
\begin{split}
\dot x_1(t)&=x_2;\\
\dot x_2(t)&=u=x_3;\\
\dot x_3(t)&=-A_1\tg b_1x_3 +x_4;\\
\dot x_4(t)&=\dot y(t)=u_1.
\end{split}\qquad
(2.109)$$Введем первую макропеременную
$$
\psi_1=x_4 +u_2(x_1,x_2,x_3)\qquad
(2.110)$$и на основе уравнения вида (2.108) при $k=1$, т.е.
$$
T_1\dot\psi_1(t) +\psi_1=0,
$$находим с учетом уравнений объекта (2.109) условное управление
$$
u_1=-\frac{\partial u_2}{\partial x_1}x_2 -\frac{\partial u_2}{\partial x_2}x_3 -\frac{\partial u_2}{\partial x_3} \big(x_4-A_1\tg b_1 x_3\big)-\frac 1{T_1}x_4 -\frac 1{T_1} u_2(x_1,x_2,x_3).\qquad
(2.111)$$Управление $u_1$ (2.111) переводит изображающую точку в окрестность многообразия $\psi_1=0$ (2.110), уравнения движения вдоль которого имеют вид
$$
\dot x_{1\psi_1}(t)=x_{2\psi_1}; \quad \dot x_{2\psi_1}(t)=x_{3\psi_1}; \quad \dot x_{3\psi_1}(t)=-A_1\tg b_1x_3 -u_2.\qquad
(2.112)$$Вводим теперь вторую макропеременную
$$
\psi_2=x_3+\beta_1x_1+\beta_2x_2\qquad
(2.113)$$и на основе уравнения
\$$
T_2\dot\psi_2(t) +\psi_2=0,
$$с учетом уравнений (2.112) находим управление
$$
u_2=\frac{\beta_1}{T_2}x_1 +\left(\beta_1 +\frac{\beta_2}{T_2}\right)x_2 +\left(\beta_2 +\frac{1}{T_2}\right)x_3-A_1\tg b_1x_3.\qquad
(2.114)$$Это управление переводит изображающую точку в окрестность многообразия $\psi_2=0$ (2.113), уравнения движения вдоль которого имеют вид
$$
\dot x_{1\psi_2}(t)=x_{2\psi_2}; \quad \dot x_{2\psi_2}(t)=-\beta_1x_{1\psi_2}-\beta_2x_{2\psi_2}.\qquad
(2.115)$$При $\beta_1=\dfrac 1{T^2}$, $\beta_2=\dfrac 2T$ дифференциальные уравнения (2.115) устойчивы и имеют кратные корни $\left(p_{1,2}=-\dfrac 1T\right )$ характеристического уравнения. Подставив $u_2$ (2.114) в (2.111) при \mbox{$T_1=T_2=T$} получаем закон управления
$$
u_1={-}\frac{x_1}{T^4}{-}\frac{4x_2}{T^3}{-}\frac{6x_3}{T^2}{-}\left(\frac{4}{T} {-}\frac{b_1A_1}{\cos^2A_1x_3}\right)x_4{-}\left(\frac{4}{T} {-}\frac{b_1A_1}{\cos^2b_1x_3}\right)A_1\tg b_1x_3.\qquad
(2.116)$$Синтезированный закон управления $u_1$ (2.116) объектом (2.109) обеспечивает ограничение $|u|\le u_{\max}=\dfrac{\pi}{2b_1}$ и апериодический характер переходных процессов по основным координатам $x_1(t)$ и $x_2(t)$ объекта. На ЭВМ для разных значений параметра $T$ было выполнено моделирование переходных процессов в замкнутой системе. На рис. 2.29 изображены переходные процессы при $T=0,5$; $b_1=\dfrac{\pi}2$ $A_1=0,05$ и начальных условиях: $x_{10}=1$, $x_{20}=x_{30}=x_{40}=0$. Время регулирования составляет $t_p\approx 4,5$ а максимальное значение координаты $x_{3\max}=u$ составляет $|0,5|<u_{\max}=1$. На рис. 2.30 для $T=1$ и тех же условий представлены соответствующие переходные процессы; при этом $x_{3\max}=|0,13|<1$. Сравнение рис. 2.22 и рис. 2.23 с рис. 2.29 и рис. 2.30 для тех параметров, начальных условий и одного и того же объекта показывает, что переходные процессы при управлениях $u_1$ (2.102) и $u_1$ (2.116) практически идентичны, во втором случае время регулирования несколько больше, что объясняется наличием дополнительного динамического звена. Однако во втором случае смягчаются условия ограничения на управление $|u|\le u_{\max}$ действующее непосредственно на исходный объект.

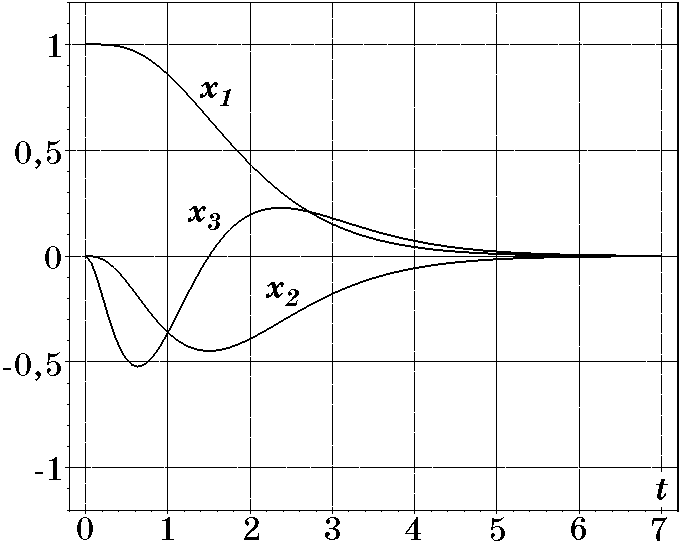
Рис. 2.29. Переходные проессы при $T=0,5$

Рис. 2.30. Переходные проессы при $T=1$

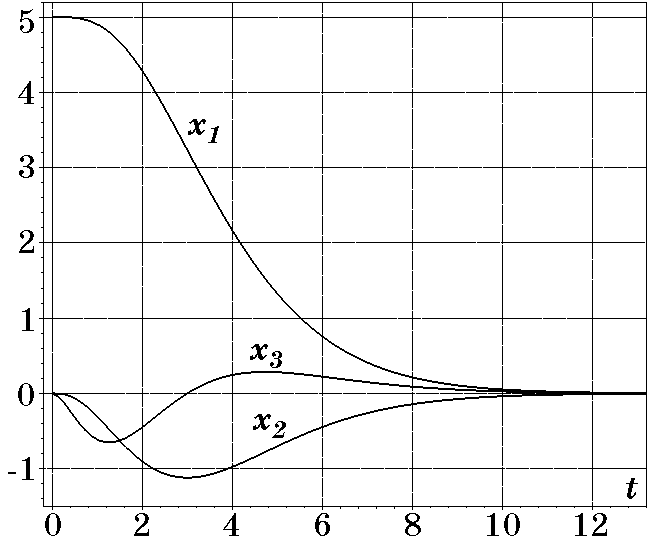
Рис. 2.31. Переходные проессы при $T=1$

 

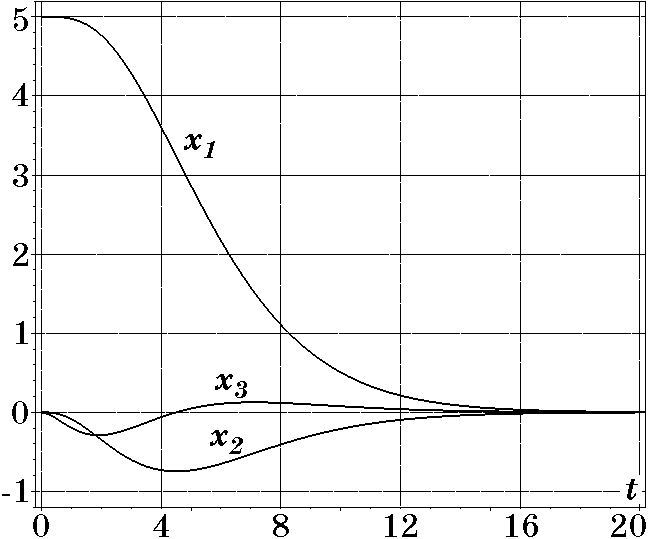
Рис. 2.32. Переходные проессы при $T=1,5$

На рис. 2.31 изображены переходные процессы в системе (2.109) с управлением $u_1$ (2.116) при $T=1$, $|u|\le 1$ и начальных условиях $x_{10}=5$, $x_{20}=x_{30}=x_{40}=0$, а на рис. 2.32 — при $T=1,5$ и тех же начальных условиях. Сравнение, например, рис. 2.25 с рис. 2.32 соответственно при управлении (2.102) в системе (2.95) и управлении (2.116) в системе (2.109) для одних и тех же начальных условий исходного объекта так же показывает идентичность переходных процессов. Однако во втором случае их время затухания несколько затянуто, но при этом смягчаются условия ограничения на управление $u(t)$. Определенным недостатком второго способа (рис. 2.27) учета ограничения $|u|\le u_{\max}$, по сравнению с первым способом (рис. 2.21), является необходимость введения дополнительного динамического звена в неизменяемой части системы.

Следует, однако, подчеркнуть, что второй способ (рис. 2.27) непосредственно применим для ограничения не только управления, но и некоторых промежуточных координат объекта. Так, если считать, что на рис. 2.27 представлена заданная неизменяемая часть системы, $u_1(t)$ является действительным управлением и необходимо ограничить некоторую координату, например, $|x_{n+1}|\le x_{n+1,\max}$, то в цепь обратной связи по этой координате следует ввести нелинейность типа $A_1\tg b_1 x_{n+1}$, что и обеспечит требуемое ограничение по рассматриваемой промежуточной координате. Разумеется, что при этом никакого расширения исходного объекта не потребуется.

Итак, предложенные здесь способы позволяют синтезировать регуляторы для нелинейных объектов при ограничениях на фазовые координаты и управления, обеспечивая при этом желаемые показатели качества замкнутой системы.

2.7.2. Ограничения на координаты в форме равенств

Перейдем теперь к изложению метода синтеза с учетом ограничений на фазовые координаты. Развитый в предыдущих главах подход к аналитическому конструированию базируется на использовании некоторых многообразий
$$
\psi_s(x_1,\dots,x_n)=0, \quad s=1,2,\dots,m\le n,\qquad
(2.117)$$к которым асимптотически притягивается изображающая точка в фазовом пространстве системы. В общем случае задаваемые притягивающие многообразия (2.117) можно трактовать как некоторые соотношения, которые желательно выдержать между координатами $x_1,\dots,x_n$ объекта в установившемся режиме движения. Такого рода задания (2.117) используются в целом ряде прикладных задач автоматического управления — в электроприводе бумагоделательных машин, где требуется поддерживать заданные соотношения между скоростями секций; в задачах управления пространственным движением тел по заданной траектории; в задаче оптимального управления движением судна с переменными условиями плавания (во льдах), сводящейся к поддержанию постоянной мощности судовой электроэнергетической установки; в задачах программного управления станками [33] и т.п. Такого рода системы называют системами функционального регулирования [151]. К формам задания вида (2.117) приводятся также и ограничения, накладываемые на координаты объекта. Ограничения можно представить в виде области $\mathcal{R}(x_1,\dots,x_n)$ фазового пространства, определяемой некоторой системой равенств или неравенств:
$$
\phi_j(x_1,\dots,x_q)=0; \quad j=1,2,\dots,p\le n; \quad q<n.\qquad
(2.118)$$Для выполнения соотношений (2.118) необходимо, чтобы число не было больше числа s управляющих воздействий в уравнениях объекта, т.е. $p\le s$. Соотношения (2.118) определяют уравнения связей между фазовыми координатами. Будем полагать, что число этих уравнений совпадает с числом управлений $m=s$. Покажем методику синтеза законов управления с учетом ограничений (2.118). Для этого следует сформировать агрегированные макропеременные следующим образом:
$$
\psi_s=\sum_{k=1}^p \beta_{sk}\phi_k(x_1,\dots,x_q) +\sum_{p=p+1}^n \alpha_{sp}x_p.\qquad
(2.119)$$Тогда в результате действия управлений $u_s$, синтезированных в соответствии с ранее изложенным методом АКАР, изображающая точка попадает на пересечение притягивающих многообразий $\psi_s=0$ (2.119) и затем будет устойчиво двигаться вдоль него. Это приведет к выполнению ограничений (2.118). Предположим, что ограничения (2.118) имеют следующий простейший вид:
$$
x_j<a_j.
$$Тогда, вводя переменные
$$
y_j(t)=x_j(t)-a_j, \quad j=1,2,\dots,p,
$$записываем соответствующие макропеременные
$$
\psi_s=\sum_{k=1}^p\beta_{sk}y_k(x_1,\dots,x_q) +\sum_{p=p+1}^n\alpha_{sp}x_p.
$$Очевидно, что после попадания изображающей точки на пересечение многообразий $\psi_s=0$ переменные $y_j(t)\to 0$, что приведет к выполнению ограничений (2.119). Изложенная процедура учета ограничений весьма проста и основана на использовании разработанного ранее метода АКАР.

Предположим теперь, что ограничения на координаты задаются в виде некоторой системы неравенств
$$
\phi_j(x_1,\dots,x_q)\le 0; \quad j=1,2,\dots,p\le n; \quad q<n.\qquad
(2.120)$$Неравенства (2.120) можно представить эквивалентными им равенствами [151]:
$$
F_j(x_1,\dots,x_q)=\big |\phi_j(x_1,\dots,x_q)\big |-\phi_j(x_1,\dots,x_q)=0.\qquad
(2.121)$$Образуя, далее, агрегированные макропеременные в виде
$$
\psi_s(x_1,\dots,x_n)=\sum_{k=1}^p\beta_{sk}F_k(x_1,\dots,x_q)+\sum_{p=p+1}^n\alpha_{sp}x_p,
\qquad(2.122)$$можно осуществить аналитический синтез законов управления с учетом ограничений, заданных неравенствами (2.120)—(2.122). При этом синтезируемые законы будут иметь переменную структуру.

Пример 3

Рассмотрим пример аналитического конструирования нелинейной системы при наличии ограничений в форме равенств на фазовые координаты. Синтезируем законы управления, обеспечивающие перевод материальной точки в центральном поле сил на круговую орбиту [71]. Дифференциальные уравнения плоского движения материальной точки в поле тяготения неподвижной притягивающей массы имеют вид [71, 72]
$$
\begin{split}
\dot x_1(t) &=x_2;\\
\dot x_2(t) &=\frac a{x_1^2} +x_1x_4^2 +\frac 1m u_1;\\
\dot x_3(t) &=x_4;\\
\dot x_4(t) &=-\frac{2x_2x_4}{x_1} +\frac{1}{bx_1}u_2.
\end{split}\qquad
(2.123)$$Здесь обозначено: $x_1(t)$, $x_3(t)$ — полярные координаты точки относительно неподвижной притягивающей массы; $x_2(t)$, $x_4(t)$ — скорость вдоль радиуса-вектора и угловая скорость вращения точки относительно центра соответственно; $a$ — постоянная; $m$ — масса материальной точки; $\psi=A\th(\beta_1x_1 +\beta_2\dot x_1) +x_3$ — управления, представляющие собой проекции реактивной силы на направление радиуса-вектора и на перпендикулярное ему направление. Необходимо синтезировать законы управления $u_1(x_1,\dots,x_n)$ и $u_2(x_1,\dots,x_n)$, обеспечивающие перевод материальной точки (2.123) из произвольного начального состояния на круговую орбиту радиуса $r$ с постоянной угловой скоростью вращения $\omega$.

Запишем указанные ограничения в виде равенств
$$
x_2 +\delta x_1 =\delta r; \quad \delta>0,\qquad
(2.124)$$
$$
x_4=\omega.\qquad
(2.125)$$Выполнение равенства (2.124) обеспечивает стремление координаты $x_1\to r$, т.к. это равенство с учетом первого уравнения объекта (2.123) можно записать в виде [72]
$$
\dot x_1(t) +\delta x_1 =\delta r,\qquad
(2.126)$$откуда следует, что
$$
x_1(t)=(x_{10}-r)e^{-\delta t} +r\to r \quad \text{при} \quad t\to\infty.
$$Выполнение же равенства (2.125) означает достижение заданной угловой скорости вращения. Выбираем следующие агрегированные макропеременные:
$$
\psi_1 =\beta_1y_1 +\beta_2y_2; \quad \psi_2=\alpha_1y_1 +\alpha_2y_2,\qquad
(2.127)$$где $y_1=x_2+\delta x_1 -\delta r$; $y_2=x_4-\omega$.

Используя функциональные уравнения
$$
T_s\dot\psi_s(t) +\psi_s=0; \quad s=1,2,
$$найдем законы управления:
$$
\begin{split}
\frac{u_1}m =&-\frac 1B\left(\frac{\beta_1\alpha_2}{T_1}-\frac{\alpha_1\beta_2}{T_2}\right)(x_2+\delta x_1 -\delta r) -\delta x_2 +\frac{a}{x_1^2}-\\
&-\frac{\alpha_2\beta_2}{B}\left(\frac 1{T_1}-\frac 1{T_2}\right)(x_4-\omega)-x_1x_4^2;
\end{split}\qquad
(2.128)$$
$$
\begin{split}
\frac{u_2}m =&-\frac{\alpha_1\beta_2}{B}\left(\frac 1{T_2}-\frac 1{T_1}\right)(x_2+\delta x_1 -\delta r)x_1 +2x_2x_4-\\
&-\frac{1}{B}\left(\frac{\beta_1\alpha_2}{T_1}-\frac{\alpha_1\beta_2}{T_2}\right)(x_4-\omega).
\end{split}\qquad
(2.129)$$где $B\neq 0$, т.е. $\dfrac{\beta_1}{\beta_2}\neq\dfrac{\alpha_1}{\alpha_2}$. Законы (2.128) и (2.129) обеспечивают перевод изображающей точки системы из произвольного начального положения на пересечение многообразий $\psi_1=0$ и $\psi_2=0$ (2.127), которое можно представить в двух формах:
$$
\psi_{12}=By_1=B(x_2+\delta x_1 -\delta r)=0
$$или
$$
\psi_{12}=By_2=B(x_4-\omega)=0,
$$которые совпадают с заданными соотношениями (2.124) и (2.125) соответственно. Поведение декомпозированной системы на пересечении многообразий $\psi_{12}=0$ описывается уравнениями
$$
\dot x_{1\psi}(t)=-\delta(x_{1\psi}-r) \quad \text{и}\quad \dot x_{3\psi}(t)=\omega,
$$первое из которых совпадает с (2.126). Из этих уравнений следует, что при $t\to\infty$ координата $x_{1s}=r$, а $x_3(t)=x_{30}+\omega t$. Это означает, что выполняются заданные ограничения на координаты системы.

Таким образом, законы управления (2.128) и (2.129) обеспечивают решение поставленной задачи перевода материальной точки из произвольного начального положения на заданные многообразия (2.124) и (2.125), которые представляют собой некоторые ограничения, записанные в виде равенств. Конкретно этот процесс представляет собой перевод материальной точки из произвольного начального состояния на круговую орбиту и дальнейшее устойчивое движение на ней. Время попадания на круговую орбиту зависит от выбора постоянных времени $T_1$, $T_2$. При $T_1=T_2=T$ законы (2.128) и (2.129) упрощаются и принимают вид
$$
u_1=-m\left[\frac 1{T_1}(x_2+\delta x_2 -\delta r) +\delta x_2 -\frac a{x_1^2}+x_1x_4^2\right];\qquad
(2.130)$$

$$
u_2=-m\left[\frac{x_1}T(x_4-\omega)-2x_2x_4\right].\qquad
$$Эти законы управления являются частным случаем законов (2.128) и (2.129), они не зависят от коэффициентов $\beta_1$, $\beta_2$, $\alpha_1$ и $\alpha_2$. Результаты моделирования синтезированной системы управления материальной точкой при переводе ее на круговую орбиту представлены на рис. 2.33 и рис. 2.34. В работе [72] на основе построения специального уравнения, включающего в себя правые части уравнений (2.123), матрицу Якоби отображения задаваемых многообразий и некоторую устойчивую матрицу, синтезированы законы $u_1$ и $u_2$, совпадающие с законами (2.130) и (2.131), если положить в них $\lambda_1=\lambda_2=-\dfrac 1T$, где $\lambda_1$, $\lambda_2$ — элементы устойчивой матрицы. В нашем же методе процедуры синтеза весьма наглядны, просты и имеют аналитический характер. Кроме того, при этом получаются более общие законы управления (2.128) и (2.129), которые обеспечивают не только выполнение ограничений (2.124) и (2.125), но и позволяют путем выбора коэффициентов $\beta_1$, $\beta_2$, $\alpha_1$ и $\alpha_2$ придать дополнительные свойства синтезируемой системе.

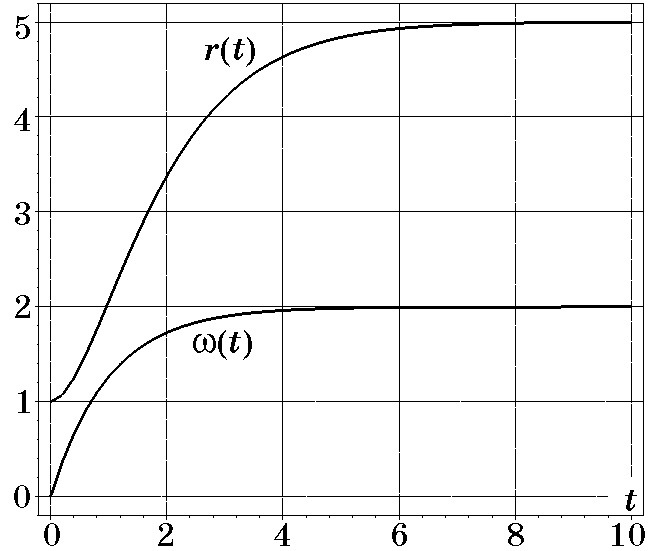
Рис. 2.33. Переходные процессы координат

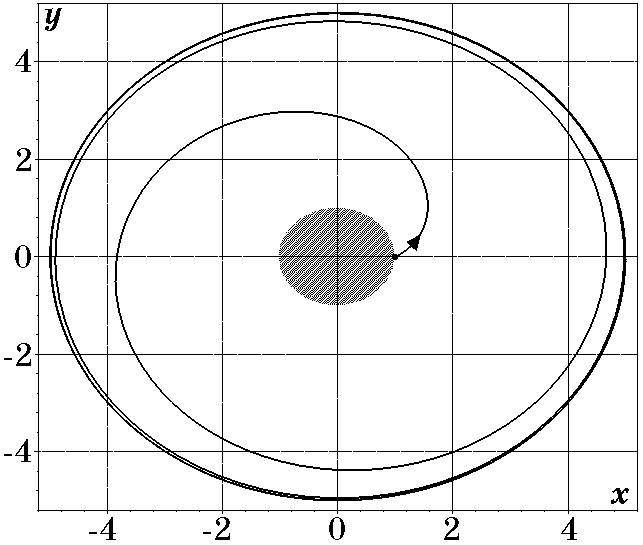
Рис. 2.34. Фазовый портрет системы

2.7.3. Многокритериальная оптимизация

Для некоторых объектов выбором функций $\psi(x_1,\dots,x_n)$ и $\th \psi$ в функциональных уравнениях можно сразу образовать оптимизирующие функционалы, являющиеся аналогами критериев быстродействия и расхода энергии в режимах больших отклонений и квадратичными критериями для режимов малых отклонений.

Пример 4

В качестве примера рассмотрим синтез системы управления объектом, состоящим из $(n-1)$ инерционных и одного интегрирующего звеньев, т.е. описываемым уравнениями
$$
\begin{split}
&T_1\dot x_1(t) =k_1x_2;\\
&T_i\dot x_i(t) +x_i =k_ix_{i+1}, \quad i=2,\dots,n-1;\\
&T_n\dot x_n(t) +x_n =k_nu.
\end{split}\qquad
(2.132)$$ Выберем агрегированную макропеременную
$$
\psi=\sum_{i=1}^n\beta_ix_i, \qquad
(2.133)$$ тогда производная $\dot\psi(t)$ после подстановки $\dot x_i(t)$ из (2.132) принимает вид
$$
\dot \psi(t)=\sum_{i=1}^{n-1}\left(\frac{\beta_ik_i}{T_i} -\frac{\beta_{i+1}}{T_{i+1}}\right)x_{i+1} +\frac{\beta_nk_n}{T_n}u.\qquad
(2.134)$$Положив, в частности,
$$\frac{\beta_ik_i}{T_i}=\frac{\beta_{i+1}}{T_{i+1}},\qquad
(2.135)$$получим
\dot \psi(t)=\frac{\beta_nk_n}{T_n}u.\qquad
(2.136)$$Из соотношения (2.135) следует выражение
$$
\beta_i=\frac{T_i}{k_i\dots k_{n-1}T_n}; \quad i=1,2,\dots,n-1; \quad \beta_n=1,\qquad
(2.137)$$устанавливающее связь между коэффициентами $\beta_i$ макропеременной $\psi$ (2.133) и параметрами исходного объекта (2.132). Подставив $\psi$ (2.133) и $\dot\psi(t)$ (2.136) в СОФ
$$
J_\Sigma=\int\limits_0^\infty\left[\th^2\psi +T^2\dot\psi^2(t)\right]dt,
$$получаем критерий качества
$$
J_1=\int\limits_0^\infty\left(\th^2\sum_{i=1}^n\beta_ix_i +\frac{T^2\beta_n^2k_n^2}{T_n^2}u^2\right)dt,\qquad
(2.138)$$который в режиме больших отклонений принимает форму, сходную с критерием быстродействия и затрат энергии на управление
$$
J_{1\sup}\sim\int\limits_{t_{0\sup}}^{t_{k\sup}}\left(1+\frac{T^2\beta_n^2k_n^2}{T_n^2}u^2\right)dt.\qquad
(2.139)$$Подставив $\psi$ (2.133) в функциональное уравнение
$$
T\dot\psi(t)+\th\psi=0,
$$в силу уравнений объекта (2.132) получаем оптимальный по критерию (2.138) закон управления
$$
u=-\frac{T_n}{k_n\beta_nT}\th\sum_{i=1}^n\beta_ix_i,\qquad
(2.140)$$который в режиме больших отклонений имеет ограничение
$$
u_{\max}=\frac{T_n}{k_n\beta_nT},
$$а в режиме малых отклонений с учетом (2.137) принимает вид
$$
u_{\inf}=-\frac{T_n}{k_1k_2\dots k_nT}\left( x_1 +\frac {1}{T_1}\sum_{i=2}^nk_1k_2\dots k_{i-1}T_ix_i\right).\qquad
(2.141)$$Закон управления (2.141) точно совпадает с законом, полученным в работе А.А. Красовского [73] при синтезе следящей системы (2.132), (2.141), оптимальной по критерию обобщенной работы
$$
J_{2}=M\left[\int\limits_0^\infty x_1^2dt\right]\qquad
(2.142)$$при дополнительном условии
$$
\frac{1}{k}M\left[\int\limits_0^\infty u^2dt\right] +\left[\int\limits_0^\infty\left(\sum_{i=1}^n\alpha_ix_i\right)^2dt\right]=const,\qquad
(2.143)$$где весовой коэффициент $k$ связан с параметром $T$ следующим соотношением:
$$
k=\frac{T_1T_2^2\dots T_{n-2}^2T_n}{k_1k_2\dots k_{n-2}T},\qquad
(2.144)$$В (2.143) коэффициенты $\alpha_i$ определяются через $\beta_i$ макропеременной $\psi$ (2.133) согласно выражению
$$
\alpha_i=\frac{k_1k_2\dots k_{n-2}}{T_1T_2^2\dots T_{n-2}^2T_n}\beta_i.\qquad
(2.145)$$Приведенное соотношение (2.144) устанавливает связь между параметром $T$ в критерии (2.138) и весовым коэффициентом $k$ в критерии обобщенной работы (2.142), (2.143), а выражение (2.145) — между коэффициентами обратных связей $\beta_i$ и $\alpha_i$ при оптимизации системы соответственно по критериям (2.138) и (2.142).

Таким образом, синтезированный закон управления $u$ (2.140) в режиме больших отклонений обеспечивает для объекта (2.132) переходные процессы, субоптимальные по критерию быстродействия и расхода энергии (2.139), а в режиме малых отклонений от желаемого состояния — процессы, оптимальные по квадратичному критерию обобщенной работы (2.142), (2.143). Уравнениями вида (2.132) описывается достаточно распространенный класс промышленных объектов, электроприводов, транспортных установок, следящих систем и др. На рис. 2.35 приведены результаты моделирования системы управления объектом третьего порядка при $T_1=1$; $T_2=2$; $T_3=1$; $k_1=k_2=1$; $\beta_1=1$; $\beta_2=2$, описываемого уравнениями
$$
\begin{split}
&\dot {x}_1(t) =x_2;\\
&\dot {x}_2(t)+0,5x_2 =0,5x_3;\\
&\dot {x}_3(t)+ x_3 =u.
\end{split}\qquad
(2.146)$$Закон управления (2.140) объектом (2.146) принимает вид
$$
u=-\frac{1}{T}\th{(x_1+2x_2+x_3)}.\qquad
(2.147)$$На рис. 2.35 изображены переходные процессы в замкнутой системе (2.146), (2.147) при $x_{10}=10$; $x_{20}=x_{30}=0$; $T=0,5$, когда критерий (2.139) принимает вид
$$
J_{\sup}\sim\int\limits_{t_{0\sup}}^{t_{k\sup}}(1+0,25 u^2)dt,\qquad
(2.148)$$а на рис. 2.36 — при $x_{10}=10$; $x_{20}=x_{30}=0$; $T=1$, когда критерий (2.139) имеет вид
$$
J_{\sup}\sim\int\limits_{t_{0\sup}}^{t_{k\sup}}(1+ u^2)dt.\qquad
(2.149)$$

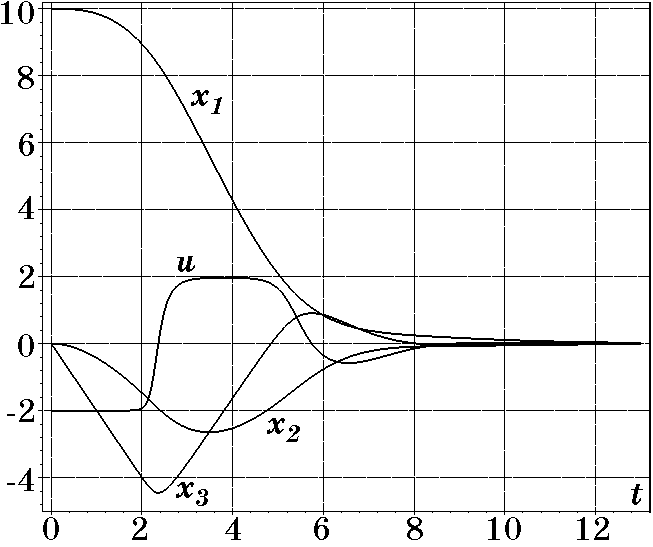
Рис. 2.35. Переходные процессы при $T=0,5$

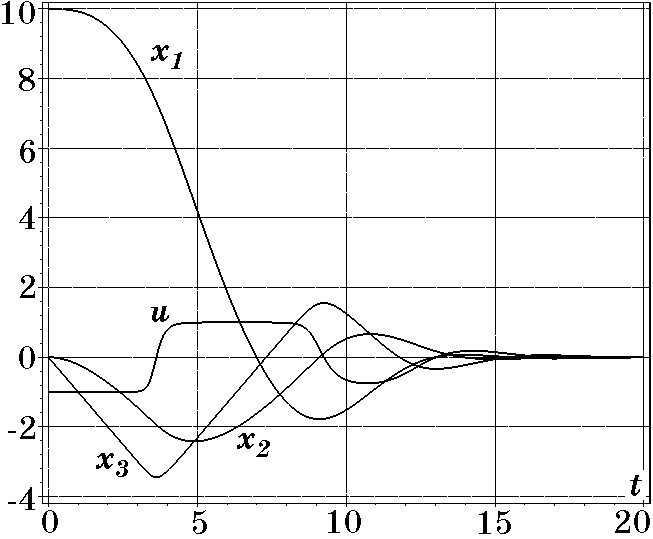
Рис. 2.36. Переходные процессы при $T=1$

Из рис. 2.35, рис. 2.36 следует, что при управлении $u$ (2.147) переходные процессы в замкнутой системе (2.146), (2.147) имеют апериодический характер, при этом для рис. 2.35, когда параметр компромисса $T=0,5$, время затухания меньше по сравнению с рис. 2.36, когда $T=1$, что соответствует виду критериев (2.148) и (2.148) в режиме больших отклонений от заданного состояния объекта. Рассмотренный здесь подход к многокритериальной оптимизации системы управления объектом (2.132) опирается на применение СОФ (2.138), который идентичен частным критериям качества (2.139) или (2.143) в соответствующих областях пространства состояний. Это означает, что СОФ (2.138) постепенно, асимптотически сходится к конкретному критерию качества, обеспечивая субоптимальные переходные процессы в системе.