Модуль 2. Общий метод аналитического конструирования нелинейных агрегированных регуляторов

2.8. Метод АКАР и бэкстеппинг

Как указывал И. Ньютон, “при изучении наук примеры не менее поучительны, чем правила”.
В этой связи, учитывая теоретическую и прикладную значимость рассматриваемой в книге проблемы системного синтеза для современной теории управления, важно произвести сравнение метода АКАР с различными методами аналитического конструирования регуляторов на конкретных примерах синтеза систем. Разумеется, что такое сравнение тех или иных методов лучше всего проводить для объектов, обладающих особыми свойствами, например желательно, чтобы они были нелинейными и многомерными. В этом отношении нет особого смысла показывать какие-то т.н. “достоинства” тех или иных методов синтеза линейных систем, как это до сих пор продолжается в работах многих авторов! Методы синтеза линейных систем — это вчерашний день теории управления. В этой связи использование метода АКАР для синтеза линейных регуляторов имеет смысл только с точки зрения демонстрации его методических преимуществ. В современной литературе трудно указать метод синтеза нелинейных систем, полностью сравнимый по своей эффективности с методом АКАР. К достаточно популярным методам нелинейного синтеза в настоящее время относится т.н. “бэкстеппинг”. Однако его определенная эффективность проявляется в основном в простых скалярных случаях синтеза нелинейных систем.

В западной научной литературе [74, 75] известен метод нелинейного преобразования координат динамических систем, математическая модель которых может быть представлена одной из возможных \textit{канонических} форм. Предположим, что математическая модель объекта с одним входом представлена в виде системы дифференциальных уравнений:
$$
\dot{\mathbf x}(t)=\mathbf{A(x)+B(x)}u; \quad y=h(\mathbf x),\qquad
(2.150)$$
где $\mathbf A(\cdot)$, $\mathbf B(\cdot)$, $h(\cdot)$ — дифференцируемые нелинейные функции своих аргументов; $u$ — скалярное управление; $y$ — измеряемый выход объекта.

Тогда можно поставить задачу приведения модели исходного объекта (2.150) к некоторой “типовой” форме. Эта задача решается применением такого преобразования $z=\Gamma(x)=col\big(\gamma_1(x),\dots,\gamma_n(x)\big)$ координат объекта (2.150), чтобы уравнение состояния в новых переменных перешли в одну из возможных канонических форм, в частности, линейную в виде системы уравнений Коши. Для объекта (2.150) такой формой может служить система уравнений [76]:
$$
\dot{z}_1(t)=z_2, \quad \dot{z}_2(t)=z_3,\dots,\dot{z}_{p-1}=z_p; \quad \dot{z}_p(t)=a(\mathbf x)+b(\mathbf x)u.\qquad
(2.151)$$Более общей является каноническая форма:
$$
\begin{split}
&\dot{z}_1(t)=z_2, \quad \dot{z}_2(t)=z_3,\dots,\dot{z}_{p-1}=z_p; \quad \dot{z}_p(t)=a(\mathbf x)+b(\mathbf x)u;\\
&\dot{z}_{p+1}(t)=\phi_{p+1}(\mathbf z);\dots;\dot{z}_n=\phi_n(\mathbf z).
\end{split}\qquad
(2.152)$$где $\mathbf z\in \mathcal{R}^n$ — новый вектор состояния объекта (2.150).
Здесь функции $\phi_j(\cdot)$ необходимо определить, а новые переменные $z_k$, $k=\overline{1,p}$ находятся по формуле [76]:
$$
z_k=\gamma_k(\mathbf x)=L_f^k h=L_f\Big(L_f\dots\big(L_f(h(\mathbf x))\big)\Big),\qquad
(2.153)$$где $L_fh=\partial h/\partial \mathbf{xA(x)}$ производные Ли функции выхода $h$ по векторному полю $\mathbf{A(x)}$ системы (2.150).
Искомые функции $\phi_i(\mathbf z)$, $p+1\le i \le n$ в (2.151) выбирают как
$$
\phi_i(\mathbf z)=L_f\gamma_i\big(\Gamma^{-1}(\mathbf z)\big).\qquad
(2.154)$$
Преобразования $\gamma_k(\mathbf x)$ (2.153) и $\phi(\mathbf z)$ (2.154) должны быть таковы, чтобы обратимое отображение $\Gamma(\mathbf x)$ удовлетворяло соотношению: $L_g\gamma_i(\mathbf x)=0$, т.е. требуется выполнение условий:
$$
\mathrm{rank}\, \Gamma(\mathbf x)=n,\qquad
(2.155)
$$
L_g\gamma_i(\mathbf x)=0.\qquad
(2.156)$$

В рассматриваемом методе [74, 75] выбор функций $\gamma_i$, удовлетворяющих условиям (2.155), (2.156), показывает принципиальную возможность приведения исходных уравнений движения объекта (2.150) к желаемой канонической форме (2.151) или (2.152). Такое преобразование координат в литературе получило название “feedback linearizable form”, т.е. линеаризация обратной связью или “точная” линеаризация уравнений объекта. Указанное преобразование означает, что можно найти некоторый закон обратной связи, обеспечивающий для объекта (2.150) в новой системе координат линейную динамику. Отличительной особенностью применения метода преобразования координат является необходимость выполнения рангового ограничения (2.155), (2.156) ($\mathrm{rank}\, \Gamma(\mathbf x_0)=n$), предполагающего существование обратного (гладкого) отображения $\mathbf x=\Gamma^{-1}(\mathbf z)$ в окрестности точки $\mathbf x_0$. Такие условия выполняются далеко не всегда, в частности, для объекта (2.150) эти условия могут не выполняться при $p<n$. Сама по себе процедура поиска преобразования $\Gamma(\mathbf x)$ трудоемка, а уравнения объекта (2.150) часто не могут быть полностью сведены к линейным уравнениям типа (2.151), которые нередко остаются нелинейными, хотя и более упрощенной структуры.

В известном обзоре [76] задача синтеза законов управления нелинейными динамическими объектами (2.150), сводимыми путем описанного выше преобразования к уравнениям вида (2.151) или (2.152), названа задачей АКАР-ОИ. Суть аббревиатуры “АКАР-ОИ” сводится к следующему. Дело в том, что термин АКАР — аналитическое конструирование агрегированных регуляторов был впервые предложен в известных работах [77—83], а термин “ОИ — бэкстеппинг, т.е. обход интегратора (integrator backstepping)”, — в работах [84—86]. В [76] утверждается, что оба метода — АКАР и ОИ для объектов вида (2.151) приводят к аналогичным законам управления. Действительно, для простейших нелинейных объектов, сводимых к структуре вида (2.151) или (2.152) из последовательно включенных интеграторов, охваченных обратными связями, оба метода формально приводят к совпадающим результатам. Однако это относится только лишь к простейшей, скалярной версии метода АКАР [79—81], который был предложен значительно ранее метода “ОИ”. Что же касается векторной версии метода АКАР, впервые предложенной еще в работе [82], то такого аналога в методе “ОИ” практически не существует. Отметим, что в известном обзоре П. Кокотовича [87] “бэкстеппинг”, на котором основан метод ОИ, отнесен к числу т.н. “эпохальных нововведений” теории управления 90-х годов XX века.

Следуя работе [76], конкретизируем метод синтеза нелинейных законов управления на основе процедуры АКАР-ОИ. Пусть для нелинейного объекта
$$
\dot {x}_1(t)=f(x_1)+g(x_1)u, \quad x_1, u \in \mathcal{R}\qquad
(2.157)$$найдено управление $u=\alpha_1(x_1)$, обеспечивающее асимптотическую устойчивость относительно $x_1=0$. Это устанавливается с помощью функции Ляпунова $V(x_1)$, производная которой по времени в силу (2.157) удовлетворяет следующему соотношению:
$$
\frac{\partial V(x_1)}{\partial x_1}\big[f(x_1)+g(x_1)\alpha_1(x_1)\big]\le -W(x_1),\qquad
(2.185)$$
где $W(x_1)$ — положительно определенная функция. Тогда для системы
$$
\begin{split}
\dot{x}_1(t) &=f(x_1)+g(x_1)x_2,\\
\dot{x}_2(t) &=u,
\end{split}\qquad
(2.159)$$где переменная $x_2$ доступна прямым измерениям, управление вида
$$
u=-\big(x_2-\alpha_1(x_1)\big)+\frac{\partial \alpha_1}{\partial x_1}\big[f(x_1) +g(x_1)x_2\big]-\frac{\partial V(x_1)}{\partial x_1}g(x_1)\qquad
(2.160)$$обеспечивает ограниченность $x_1(t)$, $x_2(t)$ и стремление $x_1\to 0$, $(x_2-\alpha_1)\to 0$ при $t\to\infty$.
Введем теперь в рассмотрение агрегированную макропеременную $\psi_1\overset{\Delta}=x_2-\alpha_1(x_1)$ и перепишем (2.159) в виде

\begin{split}
\dot{x}_1(t) &=f(x_1)+g(x_1)\big(\alpha_1(x_1)+\psi_1\big),\\
\dot{\psi}_1(t) &=u-\frac{\partial \alpha_1}{\partial x_1}\big[f(x_1) +g(x_1)x_2\big].
\end{split}\qquad
(2.161)$$

Тогда производная по времени функции Ляпунова $V_1=V(x_1)+\dfrac{1}{2}\psi_1^2$ в силу (2.160), (2.161) будет иметь вид:
$$
\dot{V}(t) =\frac{\partial V(x_1)}{\partial x_1}[f+g\alpha_1]+\frac{\partial V(x_1)}{\partial x_1}g\psi_1-\psi_1^2-\frac{\partial V(x_1)}{\partial x_1}g\psi_1%\le\\
\le -W(x_1)-\psi_1^2.\qquad
(2.162) $$Неравенство (2.162) следует из теоремы Ла Салля [76].

Пример 5

Для сравнительной иллюстрации методов АКАР и обхода интегратора рассмотрим задачу синтеза стабилизирующего управления нелинейным объектом вида
$$
\dot{x}_1(t)=x_2, \quad \dot{x}_2(t)=\sin x_1 +x_3, \quad \dot{x}_3(t)=u.\qquad
(2.163)$$В соответствии с методом ОИ на 1-м шаге вводится макропеременная вида $\psi_1=x_1$ и первая функция стабилизации (внутреннее управление) выбирается в виде $\alpha_1=-\psi_1=-x_1$. Назначая первую функцию Ляпунова $V_1=1/2x_1^2$ и вводя вторую макропеременную $\psi_2=x_2-\alpha_1$, определяем вторую функцию стабилизации [76]
$$
\alpha_2=-\psi_2 +\frac{\partial \alpha_1}{\partial x_1}x_2 -\frac{\partial V_1}{\partial x_1} -\sin x_1 =-2x_1-2x_2-\sin x_1.
$$Выбирая далее $V_2=V_1+1/2 \psi_2^2$ и вводя третью макропеременную $\psi_3=x_2-\alpha_1$, определяем действительный закон управления:
$$
\begin{split}
u&=-\psi_3+\frac{\partial \alpha_2}{\partial x_1}x_2+\frac{\partial \alpha_2}{\partial x_2}(\sin x_1+x_3)-\frac{\partial V_1}{\partial x_1}-\frac{\partial V_1}{\partial \psi_2}=\\
&=-4x_1-(5+\cos x_1)x_2-3x_3-3\sin x_1.
\end{split}\qquad
(2.164)$$В соответствии с методом АКАР синтез стабилизирующего управления осуществляется в обратном порядке. Сначала вводится макропеременная вида $\psi_1=x_3-\alpha_2$ и задается сопровождающий функционал:
$$
J_1=\int\limits_0^\infty \big[m_1^2\psi_1^2+c_1^2\dot\psi_1^2(t)\big]dt,\qquad
(2.165)$$где $m_1>0$, $c_1>0$ — постоянные коэффициенты. Управление, доставляющее минимум введенному функционалу, имеет вид [81]:
$$
u=\frac{\partial \alpha_2}{\partial x_1}x_2 -\frac{\partial \alpha_2}{\partial x_2}(\sin x_1+x_3)-\frac{1}{T_1}\alpha_2,\qquad
(2.166)$$где $T_1=c_1/m_1$. Движение вдоль многообразия $\psi_1=0$ описывается уравнением:
$$
\dot{x}_{1\psi}(t)=x_{2\psi}, \quad \dot{x}_{2\psi}(t)=\sin x_{1\psi}-\alpha_2.
$$Используя вторую макропеременную:
$$\psi_2=\beta_{21}x_1 +x_2-\alpha_2,
$$
$\beta_{21}>0$, находим внутреннее управление $\alpha_2$:
$$
\alpha_2=\frac{\beta_{21}}{T_2}x_1 +\left(\beta_{21}+\frac{\partial \alpha_1}{\partial x_1}+\frac{1}{T_2}\right)x_2 +\sin x_1 +\frac{1}{T_2}\alpha_3,\qquad
(2.167)$$минимизируя функционал вида (2.165) с заменой $\psi_1$ на $\psi_2$ и $T_2=c_2/m_2$. Движение вдоль многообразия $\psi_2=0$ описывается уравнением
$$
\dot{x}_{1\psi}(t)=-\beta_{21}x_{1\psi}-u_3,
$$
и, следовательно, $\alpha_3$ может быть положено тождественно равным нулю. Тогда, найдя $\alpha_2$ (2.167) и подставив его в (2.166), определяем внешний закон управления:
$$
\begin{split}
u=&-\frac{\beta_{21}}{T_1T_2}x_1-\left(\frac{\beta_{21}}{T_1}+\frac{\beta_{21}}{T_2}+\frac{1}{T_1T_2}+\cos x_1\right)x_2-\\
&-\left(\beta_{21}+\frac{1}{T_2}+\frac{1}{T_2}\right)x_3-\left(\beta_{21}+\frac{1}{T_2}+\frac{1}{T_2}\right)\sin x_1.
\end{split}\qquad
(2.168)$$Коэффициенты $T_1$, $T_2$ и $\beta_{21}$ могут быть выбраны для обеспечения желаемого характера и времени переходных процессов. Сравнивая (2.164) и (2.168), убеждаемся, что закон (2.168) при соответствующем выборе коэффициентов $\beta_{21}$ и $T_i$ совпадает с (2.164), т. е. методы АКАР и ОИ приводят для объекта (2.163) к законам управления одинаковой структуры [76]. Следует подчеркнуть, что закон управления (2.168) имеет обобщенный характер, что позволяет сформировать разные свойства замкнутой системы.

Пример 6

Применим метод АКАР для решения задачи синтеза законов управления нелинейным объектом
$$
\begin{split}
\dot{x}_1(t) &=-x_1 +x_1^3x_2^2,\\
\dot{x}_2(t) &=x_2(x_3+x_4),\\
\dot{x}_3(t) &=x_4,\\
\dot{x}_4(t) &=u.
\end{split}\qquad
(2.169)$$
Задача синтеза законов управления объектом (2.169) на основе процедуры бэкстеппинга рассмотрена в работе [87]. Введем, следуя методу АКАР, следующую макропеременную:
$$
\psi=x_3+x_4 +\alpha|x_2^m| +\beta x_2^2 +\gamma x_1^4,\qquad
(2.170)$$где $m\le 1$. Тогда, подставляя $\psi$ (2.170) в функциональное уравнение
$$
T\dot{\psi}(t) +\psi=0,
$$
в силу уравнений объекта (2.169) находим базовый закон управления
$$
u=-x_4-\big( \alpha m |x_2^m| + 2\beta x_2^2\big) (x_3 +x_4) -4\gamma x_1^4 (x_1^2x_2^2 -1)-\frac{1}{T}\psi.\qquad
(2.171)$$Этот закон переводит изображающую точку замкнутой системы (2.169), (2.170) в окрестность многообразия $\psi=0$ (2.170), движение вдоль которого описывается следующими декомпозированными уравнениями:
$$
\begin{split}
\dot{x}_{1\psi}(t) &=-{x}_{1\psi} +x_{1\psi}^3{x}_{2\psi}^2,\\
\dot{x}_{2\psi}(t) &=-\alpha x_{2\psi}|x_2^m|-\beta x_{2\psi}^3 -\gamma x_{1\psi}^4{x}_{2\psi}.
\end{split}\qquad
(2.172)$$Для определения условий асимптотической устойчивости системы (2.172) введем в рассмотрение функцию Ляпунова
$$
\mathrm V(t)=0,5 x_{1\psi}^2 +0,5 x_{2\psi}^2,
$$
производная которой в силу уравнений (2.172) равна
$$
\dot{\mathrm V}(t)=-x_{1\psi}^2-\alpha x_{2\psi}^2|x_2^m|-\beta x_{2\psi}^4-(\gamma-1)x_{1\psi}^4{x}_{2\psi}^2.\qquad
(2.173)$$Из (2.173) следует, что при выполнении условий
$$
\alpha>0; \quad \beta>0; \quad \gamma \ge 1\qquad
(2.174)$$функция $\dot{ \mathrm V}(t)$ будет определенно отрицательна для всех областей изменения координат $x_{1\psi}$ и $x_{2\psi}$. Это означает, что при выполнении неравенств (2.1v25} декомпозированная система (2.174) обладает свойством асимптотической устойчивости в целом. Отсюда следует, что и замкнутая система (2.169), (2.171) при $T>0$ будет также асимптотически устойчива относительно состояния $x_{1\psi}=x_{2\psi}=0$.

Выясним теперь условия устойчивости декомпозированной системы относительно координат $x_{3\psi}$ и $x_{4\psi}$. На инвариантном многообразии $\psi=0$ (2.170) эти координаты связаны соотношением
$$
x_{3\psi} +x_{4\psi}=-\alpha|x_{2\psi}^m| -\beta x_{2\psi}^2 -\gamma x_{1\psi}^4,\qquad
(2.175)$$откуда следует, что при $x_{1\psi}=x_{2\psi}=0$ координаты $x_{3\psi}$ и $x_{4\psi}$ на $\psi=0$ описываются уравнениями $\dot x_{3\psi}(t)=-x_{3\psi}$ и $\dot x_{4\psi}(t)=-x_{4\psi}$, т.е. $x_{3\psi}$ и $x_{4\psi}$ также стремятся к нулю.

Если же положить, например, $m=0$, то, согласно (2.173), система (2.172) остается асимптотически устойчивой относительно состояния равновесия $x_{1\psi}=x_{2\psi}=0$. Однако в этом случае, согласно процедуре метода АКАР и соотношению (2.175), координаты $x_{3\psi}=-\alpha$ и $x_{4\psi}=0$. Заметим, кстати, что модель (2.169) в своей структуре имеет два последовательно включенных на входе интегратора, что редко встречается на практике. Тогда равенство $x_{3\psi}=-\alpha$ будет означать некоторое установившееся положение координаты $x_3$ на выходе второго интегратора.
В выражениях для макропеременной $\psi$ (2.170) и закона управления (2.171) можно положить $\beta=0$, что не изменит условий асимптотической устойчивости замкнутой системы.
Если же в (2.170) и (2.171) положить $\alpha=0$, то в этом случае закон управления (2.171) примет вид
$$
\begin{split}
u_1=&-\frac {1}{T} x_3 -\left (1+ \frac{1}{T}\right) x_4 -2\beta x_2^2 \left(x_3 +x_4 +\frac{0,5}{T}\right) +\\
&+4\gamma x_1^4 -4\gamma x_1^4\left( x_1^2x_2^2 +\frac{0,25}{T}\right).
\end{split}\qquad
(2.176)$$

По своей структуре закон управления (2.176), за исключением последнего члена, совпадает с законом
$$
u_{\text{Б}}=-x_3-2x_4-x_2^2(x_3+x_4 +2) +4x_1^4,\qquad
(2.177)$$полученным в работе [87] методом “бэкстеппинг” после доказательства теорем об асимптотической устойчивости с использованием двух функций Ляпунова. Заметим, что закон управления (2.171) получен методом АКАР в результате простых аналитических процедур.

Следует отметить, что при использовании законов управления $u_1$ (2.176) и $u_{\text{Б}}$ (2.177) переходной процесс по координате $x_2$ будет затянут. Об этом свидетельствует структура уравнений системы (2.172), в которой при быстром затухании координаты $x_1$ решение второго уравнения будет слабочувствительным к малым значениям координаты $x_2$ , что и приведет к затягиванию переходного процесса.

На рис. 2.37, рис. 2.38, рис. 2.39, рис. 2.40, рис. 2.41 и рис. 2.42 приведены результаты моделирования замкнутой системы (2.169), (2.171) для различных коэффициентов закона управления $u$ (2.171), в том числе: на рис. 2.37 и рис. 2.38 для $\alpha=\beta=T=\gamma=m=1$; на рис. 2.39 и рис. 2.40 для $\alpha=10$, $\beta=0$, $T=m=1$, $\gamma=20$; на рис. 2.41 и рис. 2.42 для $\alpha=\beta=T=\gamma=1$, $m=0$. Эти результаты в полной мере подтверждают теоретические положения и эффективность метода АКАР.

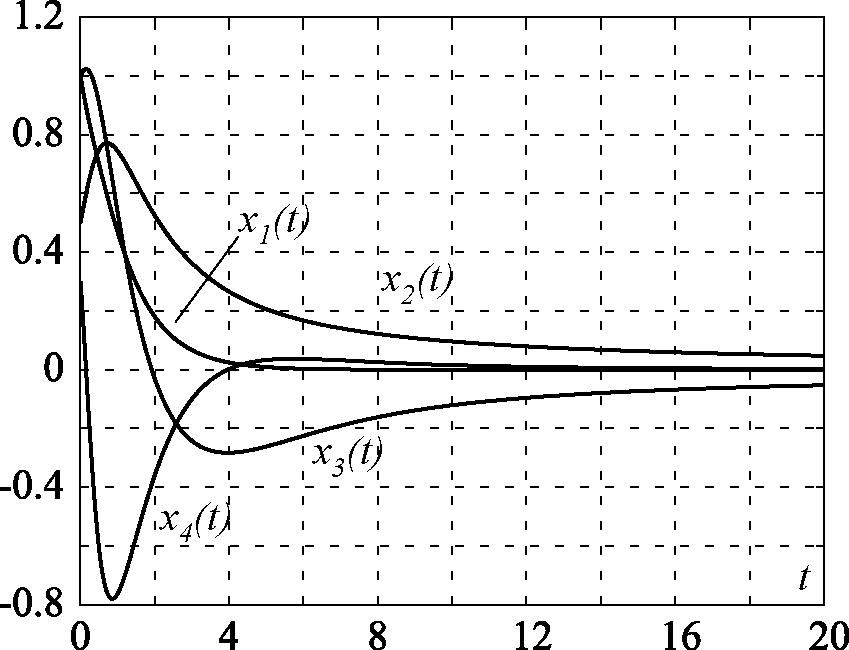
Рис. 2.37. Графики переменных состояния

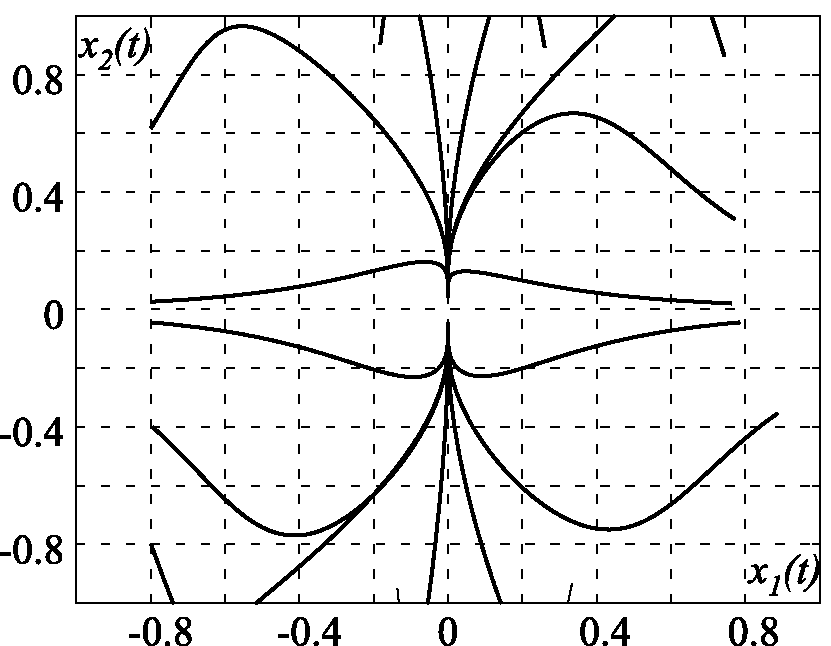
Рис. 2.38. Проекция фазового портрета

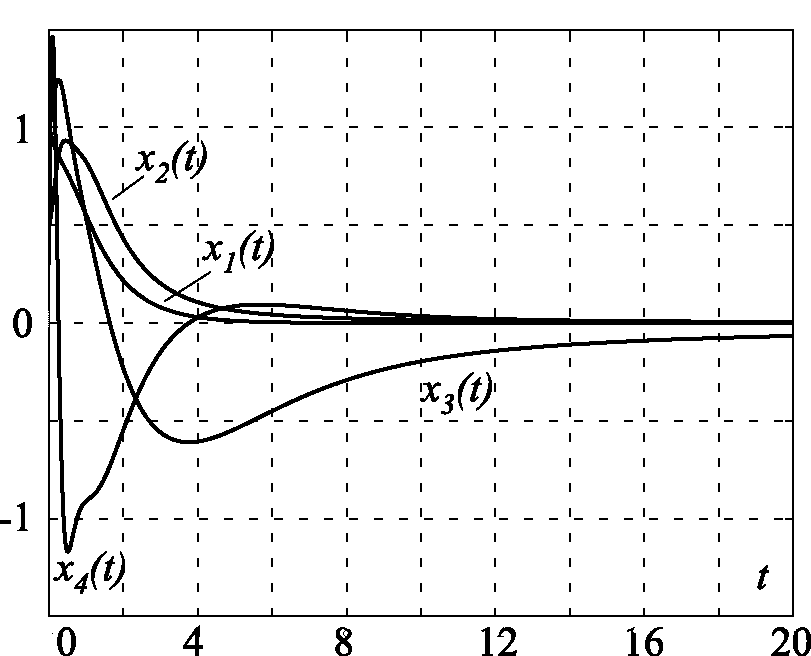
Рис. 2.39. Графики переменных состояния

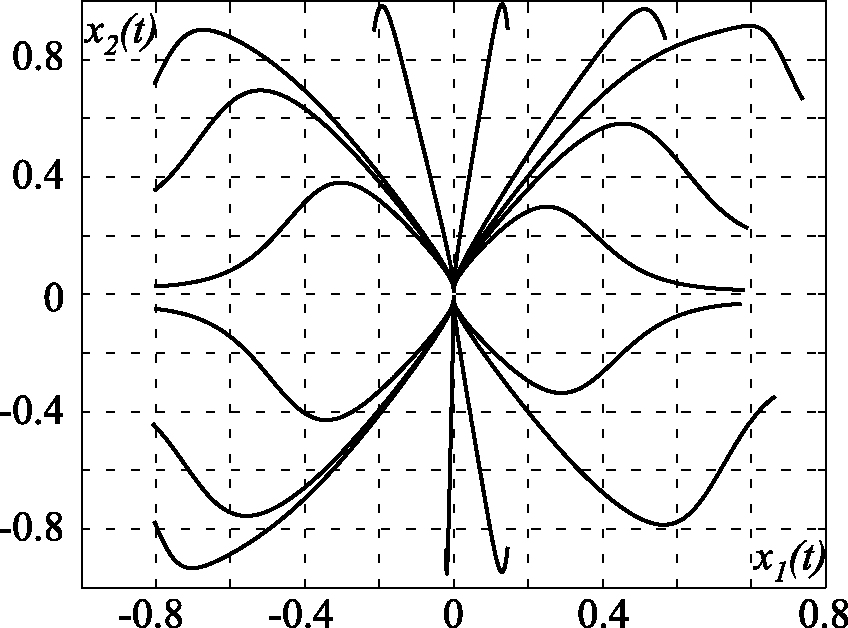
Рис. 2.40. Проекция фазового портрета

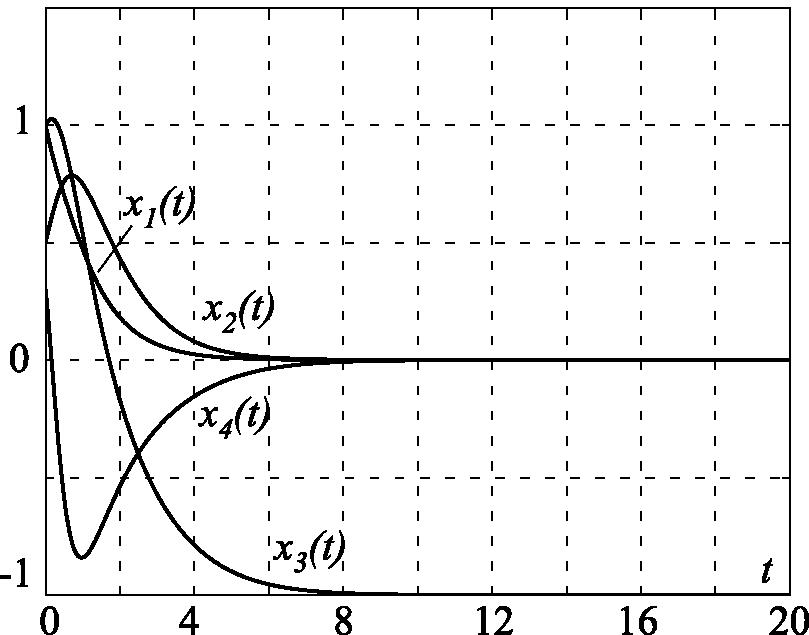
Рис. 2.41. Графики переменных состояния

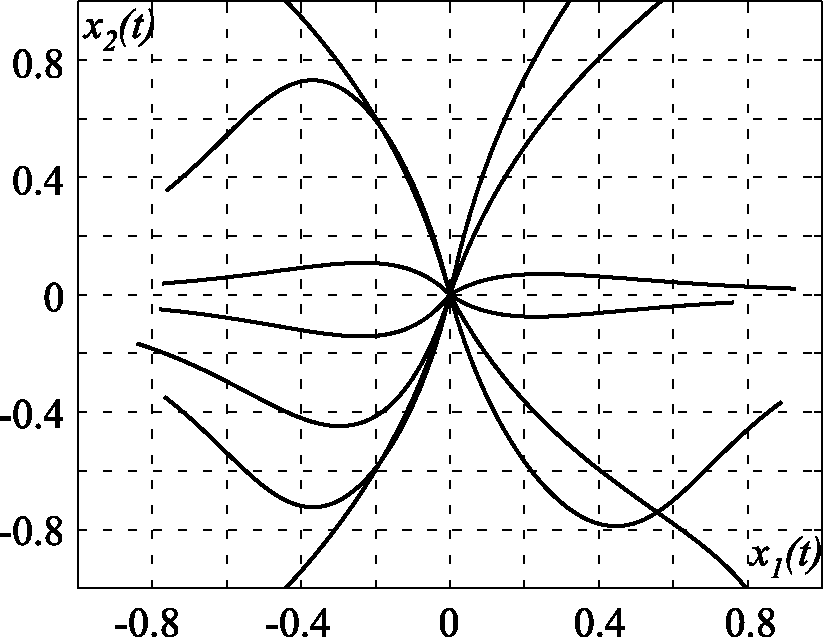
Рис. 2.42. Проекция фазового портрета

Пример 7

Как указывает П. Кокотович [87], бэкстеппинг обычно применяется к системам без обратно-прямых частей. Применение этого метода затруднено для систем, требующих повышенного быстродействия, например, вида
$$
\begin{split}
\dot{x}_1(t) =& x_2 +x_3^2,\\
\dot{x}_2(t) =& x_3,\\
\dot{x}_3(t) =&u,
\end{split}\qquad
(2.178)$$где $x_3^2$ в первом уравнении создает обратно-прямую часть в обход $x_2$ — интегратора. В этой связи Тил [88] предложил использовать аналог бэкстеппинга в виде т. н. “форвардинг — конструкции” для решения задачи управления системами типа (2.178). При этом возникают затруднения с обеспечением достаточной области устойчивости. Применим метод АКАР для решения задачи эффективного управления системами вида (2.178) с обратно-прямыми частями. Согласно методу АКАР, введем макропеременную
$$
\psi_1=x_3 +\gamma_1 x_1 +\gamma_2 x_2 +\beta_1 x_2^3.\qquad
(2.179)$$Тогда, подставляя $\psi_1$ (2.179) в функциональное уравнение
$$
T_1\dot{\psi}_1(t)+\psi_1 =0, \quad T_1>0,\qquad
(2180)$$в силу уравнений объекта (2.178) находим закон управления
$$
u_1=-\gamma_1 x_2 -\gamma_1 x_3^2 -(\gamma_2 + 3\beta_1 x_2^2)x_3 -\frac{1}{T_1}\psi_1.\qquad
(2.181)$$Закон $u_1$ (2.181) переводит изображающую точку (ИТ) замкнутой системы (2.178), (2.181) на инвариантное многообразие $\psi_1=0$, движение вдоль которого относительно координаты $x_{2\psi}$ описывается следующим дифференциальным уравнением:
$$
\ddot{x}_{2\psi}(t) +\big(\gamma_2 +3\beta_1x_{2\psi}^2 +\gamma_1\dot{x}_{2\psi}(t)\big)\dot{x}_{2\psi}(t)+\gamma_1 x_{2\psi}=0.\qquad
(2.182)$$
Условия устойчивости уравнения (2.182) и, следовательно, замкнутой системы (2.178), (2.181) имеют вид:
$$
\gamma_1>0, \quad \gamma_2>0\qquad
(2.183)$$в области малых отклонений ($\dot{x}_{2\psi}^2\approx 0$ и $x_{2\psi}^2\dot{x}_{2\psi}\approx 0$) и в области, где выполняется следующее неравенство:
$$
\gamma_2+3\beta_1x_2^2+\gamma_1x_3\ge 0.\qquad
(2.184)$$Это неравенство можно усилить при $\beta_1=0$, т. е.
$$
x_{30}>-\frac{\gamma_2}{\gamma_1}.\qquad
(2.185)$$Условия (2.184), (2.185) означают, что синтезированная система (2.178), (2.181) чувствительна к отрицательным начальным условиям по координате $x_{30}<0$ и, кроме того, введение члена $3\beta_1x_2^2$ в закон управления $u_1$ (2.181) позволяет расширить область устойчивости замкнутой системы.

В области малых отклонений уравнение (2.182) принимает форму:
$$
\tau^2\ddot{x}_{2\psi}(t)+2\xi\tau\dot{x}_{2\psi}(t) +x_{2\psi}=0,
$$
где $\xi=\dfrac{0,5\gamma_2}{\sqrt{\gamma_1}}$ — декремент затухания, $\tau=\dfrac{1}{\sqrt{\gamma_1}}$ — постоянная времени. Отсюда следует, что с увеличением коэффициента $\gamma_1$, с одной стороны, повышается быстродействие системы, однако с другой, согласно (2.184), уменьшается область устойчивости системы в случае отрицательных начальных условий по координате $x_{30}<0$. При выборе декремента $\xi=1$ между коэффициентами $\gamma_1$ и $\gamma_2$ можно установить связь $\gamma_2=2\sqrt{\gamma_1}$.

На рис. 2.43 и рис. 2.44 представлены результаты моделирования замкнутой системы (2.178), (2.181) при $\beta_1=0$ для разных начальных условий по координатам $x_{10}$, $x_{20}$, $x_{30}$ и выполнении неравенства (2.185), т.е. \mathbfox{$\gamma_2 +\gamma_1x_{30}\ge 0$}. На рис. 2.45 и рис. 2.46 представлены результаты моделирования замкнутой системы (2.178), (2.181) при $\beta=1$ и $\beta=10$ соответственно.

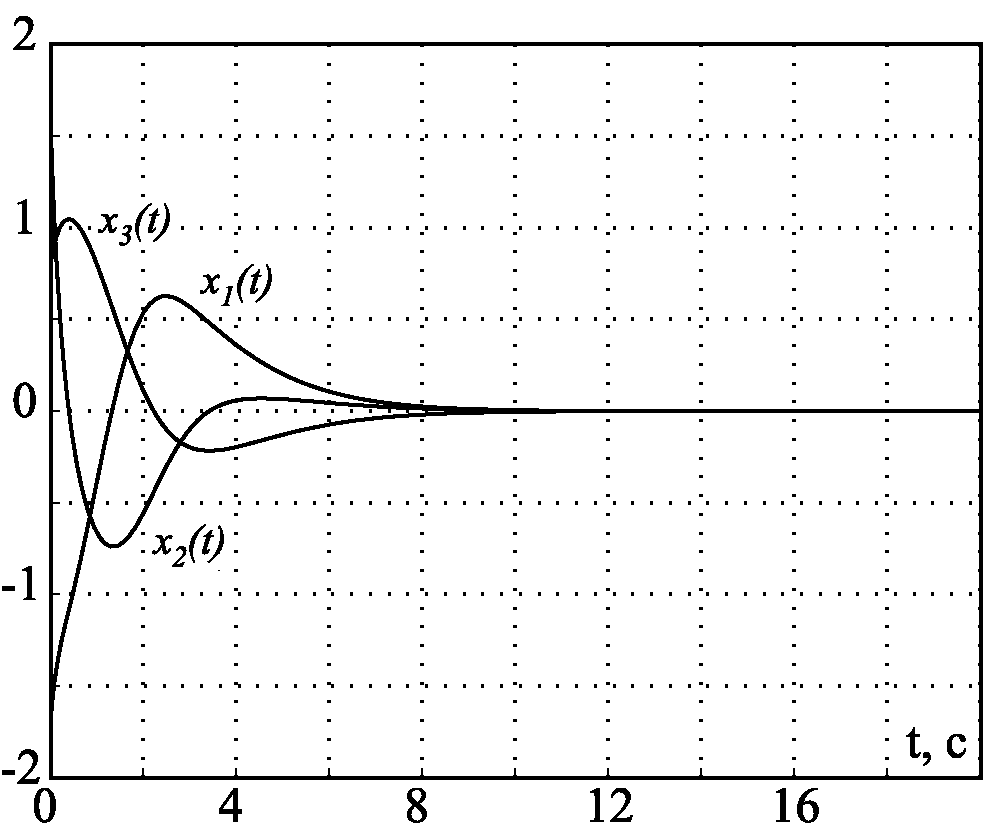
Рис. 2.43. Переходные процессы при $x_{10}=-2$, $x_{20}=2$, $x_{30}=1$

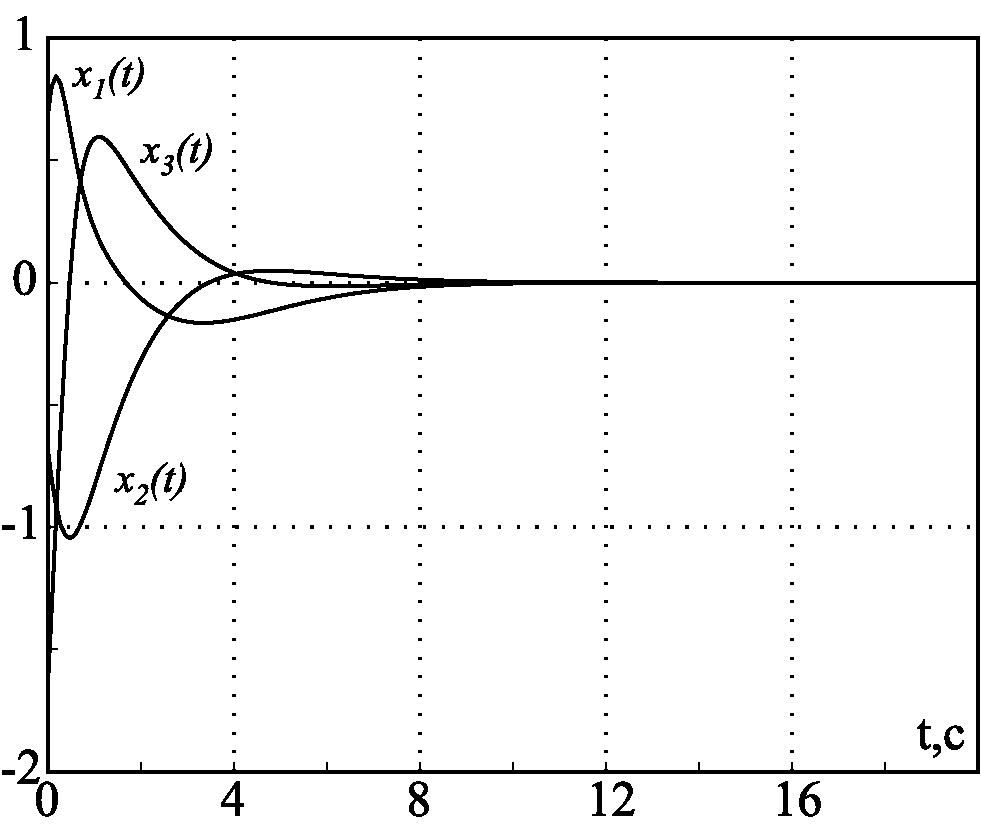
Рис. 2.44. Переходные процессы при $x_{10}=0,7$, $x_{20}=-0,8$, $x_{30}=-2$

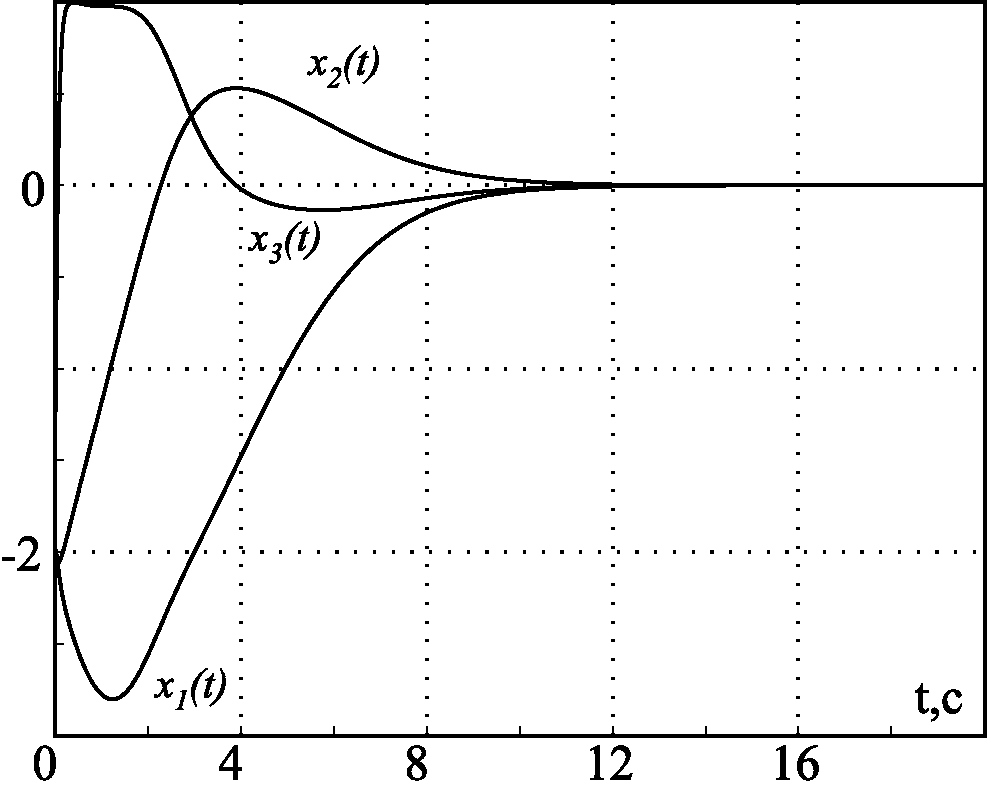
Рис. 2.45. Переходные процессы при $\beta=1$

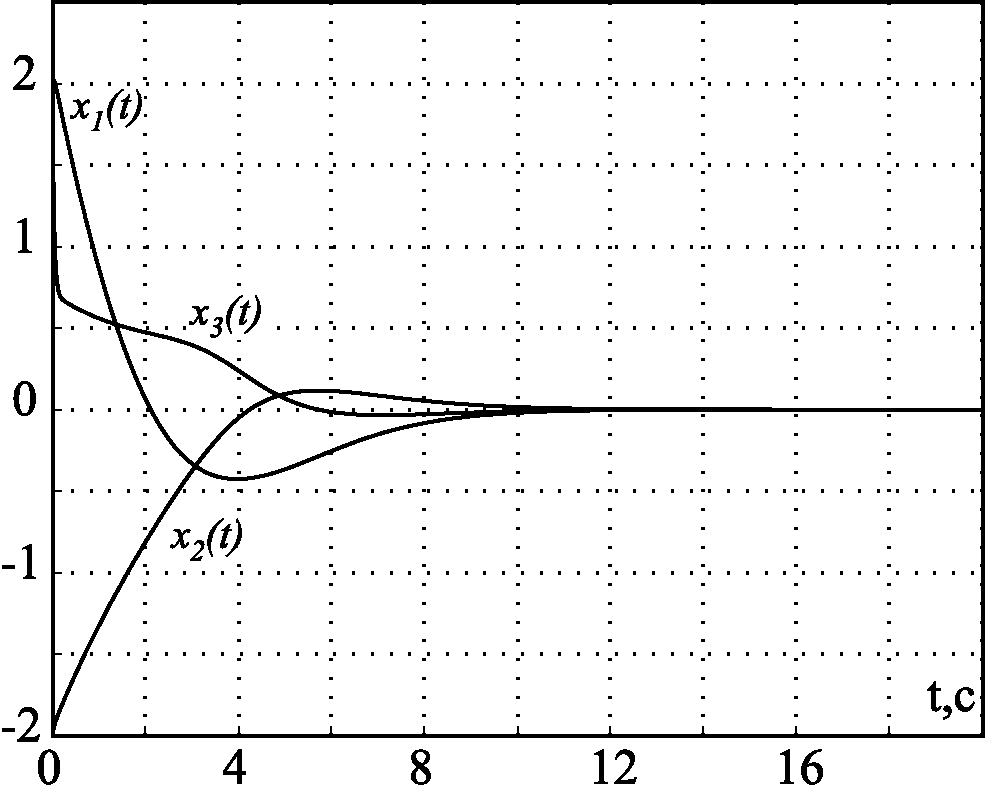
Рис. 2.46. Переходные процессы при $\beta=10$

Из условия (2.184) следует, что синтезированная система с управлением (2.181) наиболее чувствительна к отрицательным начальным условиям по координате $x_{30}<0$. В этом случае при нарушении условия (2.184) система становится неустойчивой. Для усиления условий устойчивости системы (2.178), (2.181) рассмотрим ее уравнение движения относительно координаты $x_{3\psi}$ на многообразии $\psi_1=0$ при $\beta_1=0$, т. е.
$$
\ddot{x}_{3\psi}(t) +\big(2\gamma_1x_{3\psi} +\gamma_2\big)\dot{x}_{3\psi}(t)+\gamma_1 x_{3\psi}=0,\qquad
(2.186)$$которое можно получить путем дифференцирования по времени уравнения (2.182). Очевидно, что уравнение (2.186) устойчиво относительно $x_{3\psi}=0$ при выполнении неравенства
$$
x_{3\psi 0}\ge -\frac{\gamma_2}{2\gamma_1},\qquad
(2.187)$$которое является более ограничительным по сравнению с (2.185). Итак, для обеспечения условий устойчивости синтезированной системы (2.178), (2.181) необходимо, чтобы выполнялось неравенство (2.187). Это означает, что для выполнения условия (2.185) на координату $x_3$ следует наложить ограничение $|x_3|\le b=\dfrac{\gamma_2}{2\gamma_1}$. Для этого введем следующую макропеременную:
$$
\psi_2=x_3+b\th(\gamma_1x_1 +\gamma_2x_2 +\beta_1x_2^3).
$$
Тогда на основе функционального уравнения
$$
T_2\dot{\psi}_2(t)+\psi_2 =0
$$
и уравнений объекта (2.178) можно найти закон управления
$$
u_2=-\frac{b(\gamma_1x_2+\gamma_1x_3^2 +\gamma_2x_3 +3\beta_1x_2^2x_3)}{\ch^2(\gamma_1x_1 +\gamma_2x_2 +\beta_1x_2^3)}-\frac{1}{T_2}\psi_2.\qquad
(2.188)$$Отметим, что в физическом плане координата $x_3$ — это положение интегрирующего исполнительного механизма, которое всегда ограничено.

На рис. 2.47 приведены результаты моделирования замкнутой системы (2.178), (2.188) при $\beta_1=0$ и $x_{30}<0$, а на рис. 2.48 и рис. 2.49 — для разных $\beta_1$ и $x_{30}<0$. Эти результаты подтверждают основные теоретические положения и эффективность метода АКАР.

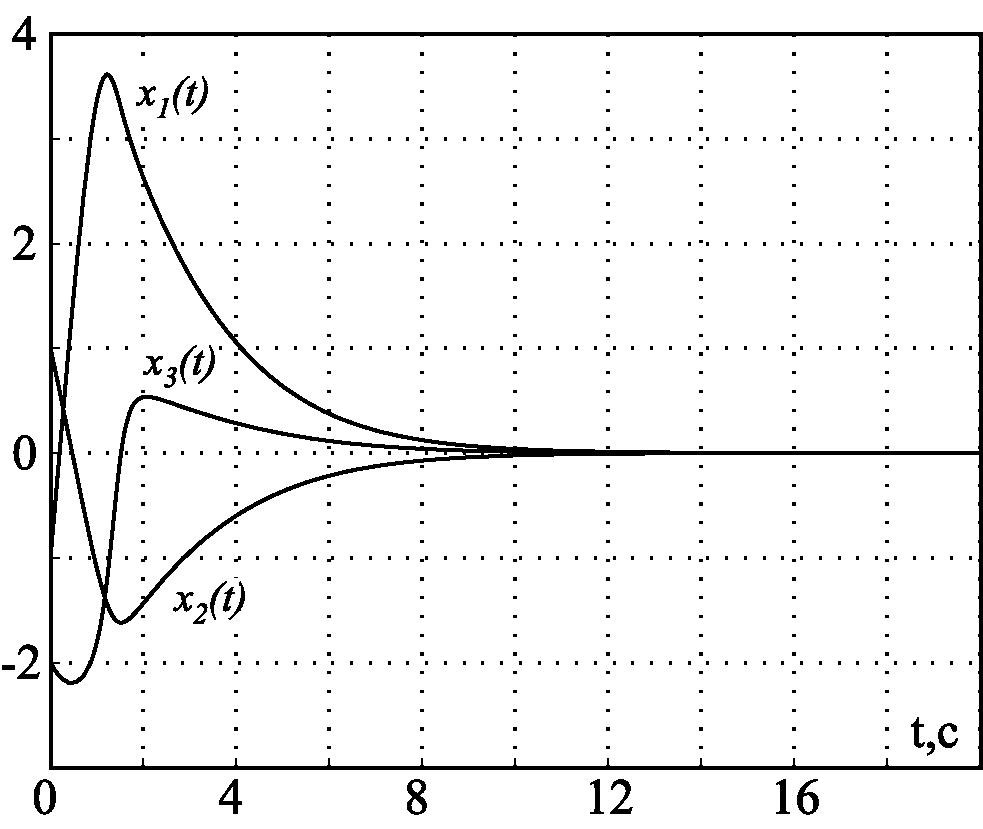
Рис. 2.47. Переходные процессы в системе с ограничениями при $\beta_1=0$

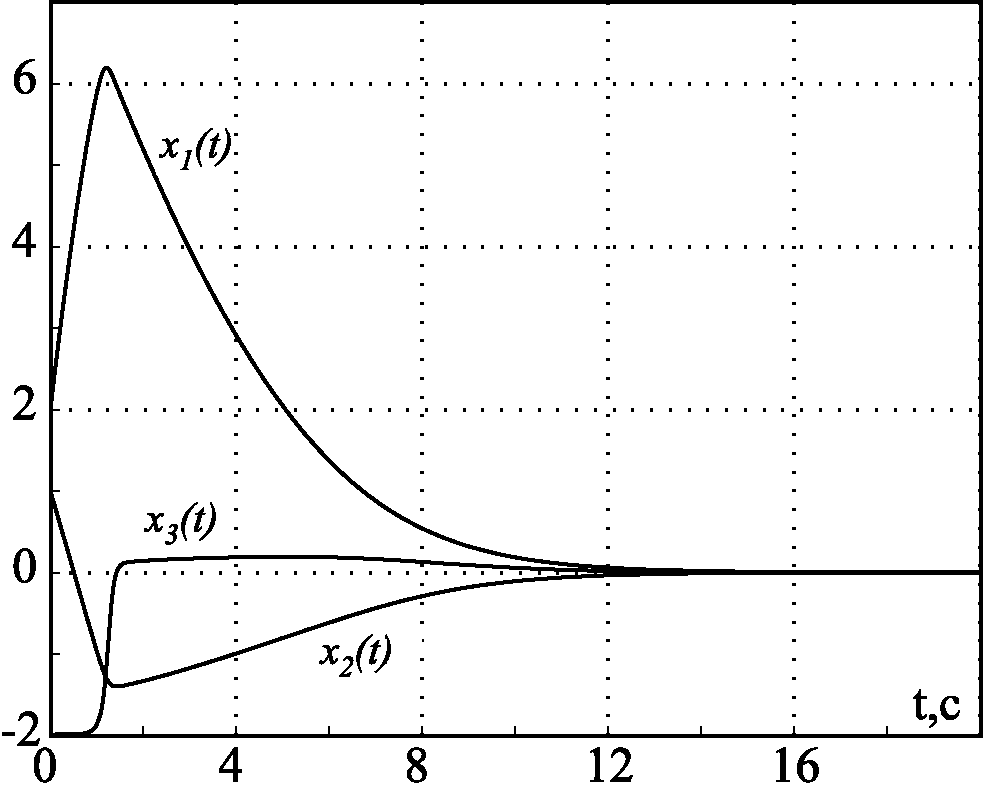
Рис. 2.48. Переходные процессы в системе с ограничениями при $\beta_1=1$

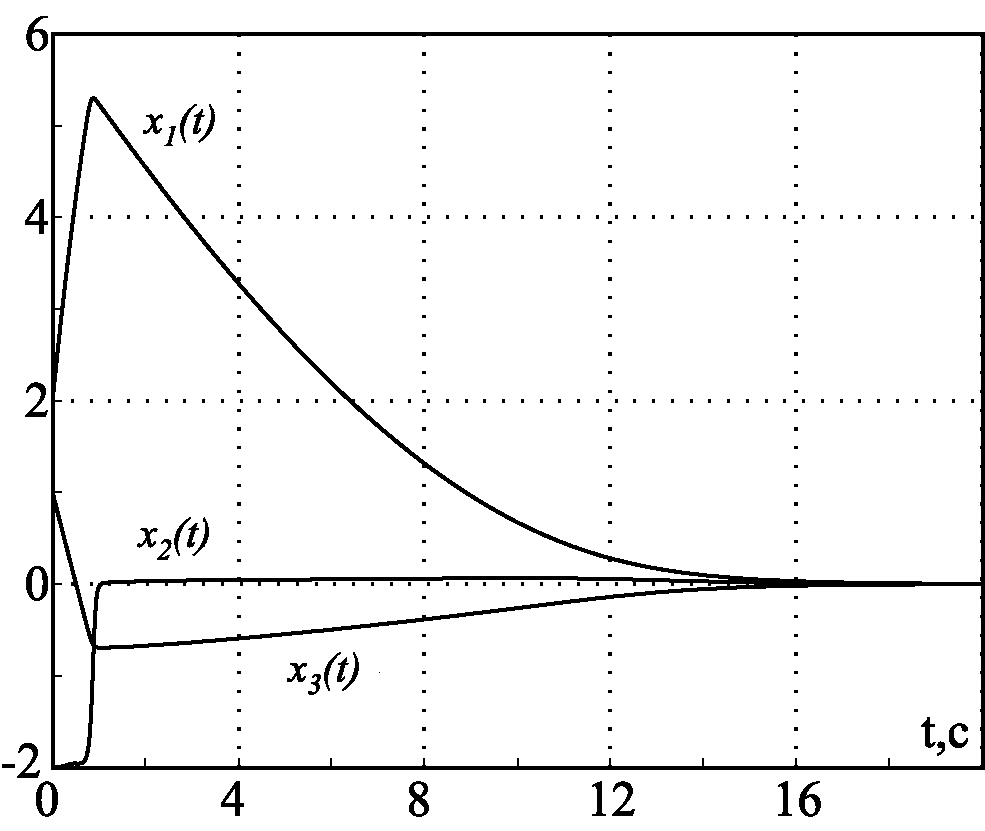
Рис. 2.49. Переходные процессы в системе с ограничениями при $\beta_1=10$

Таким образом, применение метода АКАР для управления нелинейными системами, например вида (2.178), имеющих обратно-прямую часть, позволяет аналитически синтезировать эффективные законы управления, обеспечивающие асимптотическую устойчивость замкнутым системам.

Пример 8

Следующим примером, приведенным в [87] и вызвавшим затруднения с непосредственным применением бэкстеппинга, является задача синтеза стабилизирующего закона управления нелинейным объектом
$$
\begin{split}
\dot{x}_1(t) =& x_1 +x_2 +x_3^3,\\
\dot{x}_2(t) =& x_3,\\
\dot{x}_3(t) =&u,
\end{split}\qquad
(2.189)$$Объект (2.189) по своей структуре аналогичен объекту (2.178), за исключением того, что в первом уравнении системы (2.189) “обратно-прямая” часть представлена не квадратичной, а кубической нелинейностью $x_2^3$ и, кроме того, также добавлен член $x_1$. В работе [87] на основе теоремы пассивности, линейного матричного неравенства и пакета программ предложена процедура численного определения коэффициентов нелинейного закона управления
$$
u=k_1x_1 +k_2x_2 +k_3x_3 +\beta x_3^3.\qquad
(2.190)$$Покажем здесь, что задача синтеза закона управления объектом (2.189) решается методом АКАР аналитически и весьма элегантно в результате простых и ясных процедур. Согласно методу АКАР, введем следующую макропеременную:
$$
\psi_1=x_3 +\gamma_1x_1 +\sin \gamma_2x_2.\qquad
(2.191)$$Тогда на основе функционального уравнения
$$
T_1\dot{\psi}_1(t)+\psi_1 =0, \quad T_1>0,\qquad
(2.192)$$
и в силу уравнений объекта (2.189) найдем закон управления
$$
u_1=-\gamma_1(x_1 +x_2 +x_3^3) -\gamma_2x_3\cos\gamma_2x_2-\frac{1}{T_1}\psi_1.\qquad
(2.193)$$
Этот закон, согласно (2.192), через время $t=(3\div 4)T_1$ переводит ИТ замкнутой системы (2.189), (2.193) из произвольных начальных условий $x_{i0}$ в малую окрестность инвариантного многообразия $\psi_1=0$ (2.1v42}. Движение системы вдоль $\psi_1=0$ описывается относительно координаты $x_2$ дифференциальным уравнением
$$
\ddot{x}_{2\psi}(t) +\big(\gamma_2\cos \gamma_2 x_{2\psi} -1 +\gamma_1\dot{x}_{2\psi}^2(t)\big)\dot{x}_{2\psi}(t)+\gamma_1x_{2\psi}-\sin \gamma_2x_{2\psi}=0.\qquad
(2.194)$$

Декомпозированное уравнение (2.194) относится к классу уравнений маятникового типа, обладающих в зависимости от выбора коэффициентов $\gamma_1$ и $\gamma_2$ разнообразными движениями — от регулярных колебаний до апериодических переходных процессов. Дивергенция поля этого уравнения равна
$$
\mathrm{div} \dot{\mathbf x}_{2\psi}(t)=1-\gamma_2\cos \gamma_2 x_{2\psi} -3 \gamma_1\dot{x}_{2\psi}^2(t).\qquad
(2.195)$$
Из выражения (2.195) следует, что при $\gamma_2>0$ дивергенция всегда отрицательна, т. е. синтезированная система (2.189), (2.193) будет обладать некоторым притягивающим множеством.
В случае же, когда $\gamma_2<1$ и тем более $\gamma_2<0$, дивергенция может изменить свой знак при некоторых значениях переменных $x_{2\psi}$ и $\dot{x}_{2\psi}(t)$. Согласно критерию Бендиксона, это означает, что в системе имеет место предельный цикл. Действительно, произведем линеаризацию функций $\sin \gamma_2 x_2\cong \gamma_2 x_2$ и $\cos \gamma_2 x_2\cong 1$. Тогда макропеременная $\psi_1$ (2.191) и уравнение (2.194) примут соответственно вид
$$
\psi_1=x_3 +\gamma_1x_1 +\gamma_2x_2\qquad
(2.196)$$
и $$
\ddot{x}_{2\psi}(t) +\big(\gamma_2 -1 +\gamma_1\dot{x}_{2\psi}^2(t)\big)\dot{x}_{2\psi}(t)+(\gamma_1-\gamma_2)x_{2\psi}=0.\qquad
(2.197)$$
Уравнение (2.197) — это известное в теории нелинейных колебаний уравнение Релея, которое при $\gamma_1>\gamma_2$ и $\gamma_2<1$ или $\gamma_2<0$ обладает одним устойчивым предельным циклом, а при $\gamma_2\ge 1$ будет асимптотически устойчивым относительно $x_{2\psi}=\dot{x}_{2\psi}(t)=0$. В этом случае, согласно (2.196), закон управления (2.193) принимает частный вид
$$
u_1=-\gamma_1\left(1+\frac{1}{T_1}\right)x_1 -\gamma_2\left(1+\frac{1}{T_1}\right)x_2 -\left(\gamma_2+\frac{1}{T_1}\right)x_3 -\gamma_1x_3^3,\qquad
(2.198)$$который по своей структуре совпадает с законом (2.190), полученным в [87] на основе процедуры бэкстеппинга. Отметим, что закон (2.198) получен в результате простых аналитических процедур, а выбор его коэффициентов непосредственно связан со свойствами нелинейного декомпозированного уравнения (2.197), которое при $\gamma_1>\gamma_2>1$ будет асимптотически устойчивым. В режиме малых отклонений уравнение (2.197) имеет декремент затухания
$$
\xi=\frac{0,5(\gamma_2 -1)}{\sqrt{\gamma_1-\gamma_2}}, \quad \gamma_1>\gamma_2>1.\qquad
(2.199)$$Если в (2.199) положить $\xi=1$, то между коэффициентами $\gamma_1$ и $\gamma_2$ можно установить следующую связь:
$$
\gamma_1=\gamma_2+0,25(\gamma_2-1)^2.\qquad
(2.200)$$
Выражения (2.199) и (2.200) позволяют выбрать коэффициенты закона управления $u_1$ (2.198), т. к. член $\gamma_1\dot{x}_{2\psi}^2$ усиливает демпферные свойства системы (2.197).

Если же представить функции $\sin\gamma_2x_2$ и $\cos\gamma_2x_2$ разложениями $\sin\gamma_2x_2\cong \gamma_2x_{2\psi}-\dfrac{\gamma_2^3}{6}x_{2\psi}^3$ и $\cos\gamma_2x_2\cong 1-0,5\gamma_2^2x_{2\psi}^2$, то макропеременная $\psi_1$ (2.191) и уравнение (2.194) приобретут формы
$$
\psi_1=x_3+\gamma_1x_1+\gamma_2x_{2\psi}-\frac{\gamma_2^3}{6}x_{2\psi}^3\qquad
(2.201)$$
и $$
\ddot{x}_{2\psi}(t) +\Big[\gamma_2\big(1-0,5\gamma_2^2x_{2\psi}^2\big)-1+\gamma_1\dot{x}_{2\psi}^2(t)\Big]\dot{x}_{2\psi}(t) %+\\
+\gamma_1-\gamma_2)x_{2\psi} + \frac{\gamma_2^3}{6}x_{2\psi}^3=0.\qquad
(2.202)$$Уравнение (2.197) можно назвать обобщенным уравнением Ван-дер-Поля — Релея — Дюффинга, оно является частным случаем уравнения (2.194) и, следовательно, также относится к маятниковому классу.

Рассмотрим теперь поведение замкнутой системы (2.189), (2.193) относительно координаты на многообразии $\psi_1=0$ (2.201). Так как, согласно (2.189), $x_3=\dot{x}_2(t)$, то продифференцировав (2.194) по времени, находим декомпозированное уравнение
$$
\ddot{x}_3(t)+\big(\gamma_2-1 +3\gamma_1x_3^2\big)\dot{x}_3(t) +(\gamma_1-\gamma_2)x_3=0.\qquad
(2.203)$$
Уравнение (2.203) при $\gamma_1<1$ и $\gamma_2<1$ или $\gamma_2<0$ является известным уравнением Ван-дер-Поля, что следует из самой процедуры его получения. Итак, при выборе линейной макропеременной $\psi_1$ (2.196) движение замкнутой системы (2.189), (2.198) на многообразии $\psi_1=0$ (2.196) описывается декомпозированными уравнениями (2.197) и (2.203) относительно координат $x_2$ и $x_3$ соответственно. Эти уравнения при соответствующем выборе коэффициентов $\gamma_1$ и $\gamma_2$ будут соответственно представлять собой уравнения Релея и Ван-дер-Поля.

На рис. 2.50 и рис. 2.51 представлены результаты моделирования, которые подтверждают теоретические положения и прикладную эффективность метода АКАР.

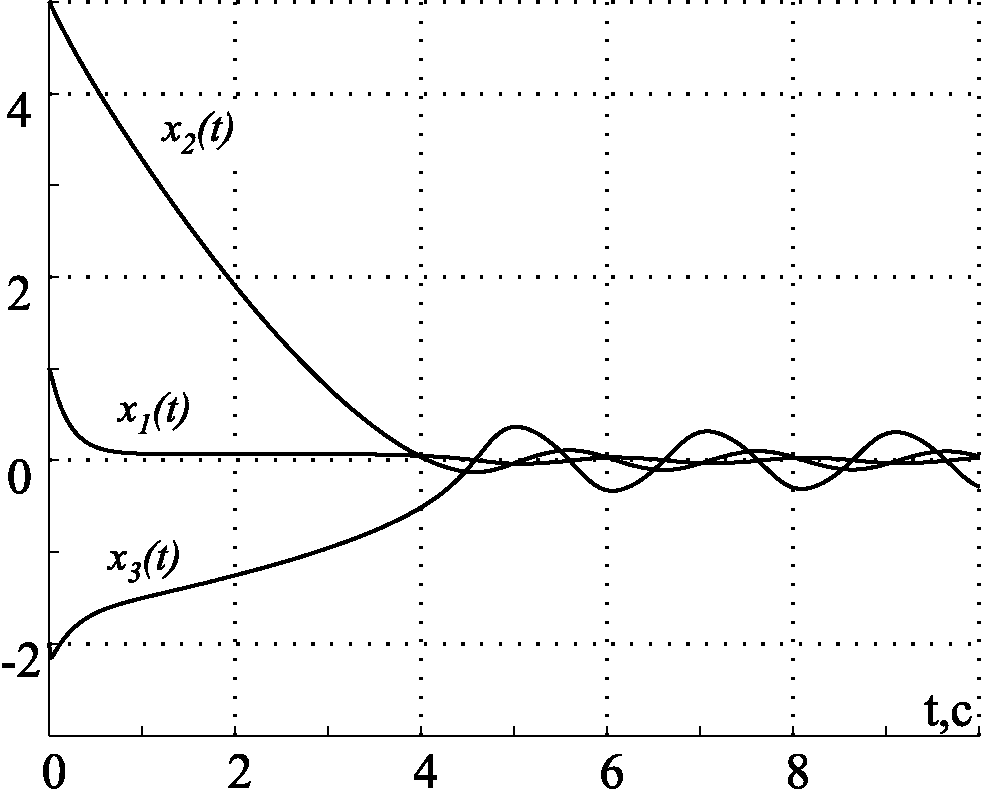
Рис. 2.50. Переходные процессы в колебательной системе

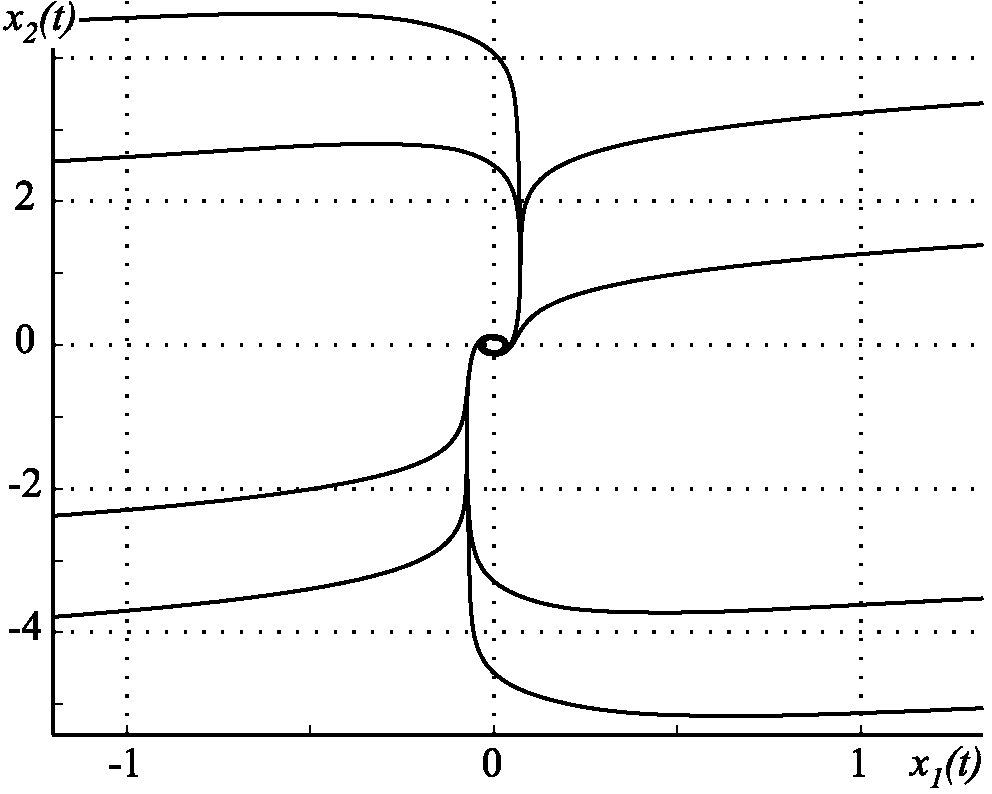
Рис. 2.51. Проекция фазового портрета в колебательной системе

Таким образом, эффективно решена задача аналитического синтеза стабилизирующих законов управления объектом (2.189). Эти законы гарантируют асимптотическую устойчивость в целом замкнутой системы и обеспечивают желаемый характер переходных процессов. Следует подчеркнуть, что дело не столько в наличии нелинейности $x_3^3$ — “обратно-прямой” части в обход $x_2$ — интегратора, на что обращается особое внимание в работе [87], а в четности или нечетности степени указанной нелинейности. Если в задаче (2.178) нелинейность ($x_3^2$) была четной степени, что привело к необходимости ограничения координаты $|x_3|\le b$ по модулю, то в задаче (2.189) указанная нелинейность ($x_3^3$) нечетной степени, что позволило весьма элегантно разрешить методом АКАР задачу синтеза стабилизирующих законов управления.

Итак, метод АКАР показал свои несомненные преимущества перед бэкстеппингом как по физической ясности постановки задачи управления, так и в отношении аналитичности и простоты процедур синтеза законов управления.