Модуль 2. Общий метод аналитического конструирования нелинейных агрегированных регуляторов

2.6. Синергетический синтез скалярных регуляторов

2.6.1. Общие положения

Метод АКАР базируется на положении, согласно которому в фазовом пространстве динамических систем могут существовать многообразия, к которым притягиваются фазовые траектории. В общем случае можно построить несколько таких многообразий, которые, очевидно, включают в себя некоторые поверхности
притяжения. Тогда возникает идея конструирования такой совокупности поверхностей притяжения, чтобы ИТ, начав двигаться из произвольного начального состояния, последовательно перемещалась от одной поверхности притяжения к другой, пока не попадет на финишную поверхность, ведущую, в частности, к началу координат фазового пространства. В этом случае ИТ сначала сближается с многообразием $\psi_1=0$, затем с $\psi_2=0$ и т.д. После сближения с последним многообразием $\psi_m=0$ организуется процесс устойчивого движения к заданному состоянию, в частности к началу координат.

В общем случае при использовании $r$ притягивающих многообразий размерность каждого $i$-го многообразия будет на единицу меньше предыдущего, т.е. ИТ сначала сближается с многообразием размерности $n-1$, затем $n-2$ и т.д., вплоть до многообразия размерности $n-r$. На последнем этапе движение к началу координат будет описываться системой дифференциальных уравнений $(n-r)$-го порядка.

В зависимости от выбранного числа $r$ притягивающих многообразий можно получить различные свойства синтезируемых нелинейных систем [61, 88].

Перейдем к математическому описанию изложенной процедуры синтеза нелинейных систем на основе введения последовательности притягивающих многообразий. Предположим, что возмущенное движение объекта описывается следующей системой нелинейных дифференциальных уравнений:
$$
\begin{aligned}
\dot {x}_i(t) &=f_i(x_1,\dots,x_n), &\; i&=1,2,\dots,p;\\
\dot {x}_j(t) &=f_j(x_1,\dots,x_j)+a_{j+1}x_{j+1}, &\; j&=p+1,p+2,\dots,n-1;\\
\dot {x}_n(t) &=f_n(x_1,\dots,x_n)+u, &\; &
\end{aligned}\qquad
(2.41)$$где $x_i$, $x_j$ — координаты состояния объекта; $f_i(x_1,\dots,x_n)$ — непрерывные функции; $f_i(0,\dots,0)=0$; $f_j(x_1,\dots,x_j)$ — непрерывные функции, дифференцируемые по своим переменным; $f_j(0,\dots,0)=0$; $u$ — управляющее воздействие.

Несмотря на некоторую специфичность рассматриваемой системы дифференциальных уравнений (2.41) этой математической моделью могут быть представлены практически важные классы различных объектов. Так, частным случаем уравнений (2.41) является система дифференциальных уравнений ($p=0$)
$$
\begin{split}
\dot x_1(t) &=f_1(x_1) +a_2x_2;\\
\dot x_2(t) &=f_2(x_2) +a_3x_3;\\
\dots\dots & \dots\dots\dots\dots\dots.\,;\\
\dot x_{n-1}(t) &=f_{n-1}(x_{n-1}) +a_nx_n;\\
\dot x_n(t) &=f_n(x_n) +u,
\end{split}
$$которой описывается широко распространенный в разных областях техники класс объектов, состоящий из последовательно включенных нелинейных динамических звеньев. К таким объектам относятся цепочки химических реакторов, различные нагревательные аппараты, транспортные и обогатительные машины, электрические, гидравлические и пневматические приводы мощных машин и др.

Перейдем к описанию метода АКАР для нелинейных объектов (2.41) с использованием совокупности последовательно вводимых инвариантных (притягивающих) многообразий. Введем в рассмотрение первую агрегированную макропеременную
$$
\psi_1=\sum_{k=1}^n\beta_{1k}x_k +\phi_1(x_1,\dots,x_{n-1}),\qquad
(2.42)$$Задача состоит в синтезе управления $u_1(x_1,\dots,x_n)$, переводящего объект (2.41) из произвольного начального состояния (в некоторой области) в окрестность многообразия (2.42). Используем для решения этой задачи функциональное уравнение
$$
T_1\dot\psi_1(t) +\psi_1=0.\qquad
(2.43)$$Тогда в соответствии с методом АКАР управление, согласно (2.42) и (2.43), будет иметь вид
$$
\begin{split}
u_1 = &-\frac 1{\beta_{1n}} \sum_{i=1}^p \left( \beta_{1i}+\frac{\partial \phi_1}{\partial x_i} \right)f_i -\frac 1{\beta_{1n}} \sum_{j=p+1}^{n-1} \left( \beta_{1j}+\frac{\partial \phi_1}{\partial x_j} \right) \times \\
&\times (f_j+a_{j+1}x_{j+1}) -\frac 1{\beta_{1n}T_1}\psi_1 -f_n.
\end{split}\qquad
(2.44)$$

Управление $u_1$ (2.44) переводит ИТ на многообразие $\psi_1=0$, движение вдоль которого описывается уравнениями:
$$
\begin{split}
\dot {x}_1(t) =& f_i(x_1,\dots,x_n), \quad i=1,2,\dots,p;\\
\dot {x}_j(t) =& f_j(x_1,\dots,x_j) +a_{j+1}x_{j+1}, \quad j=p+1,\dots,n-2;\\
\dot {x}_{n-1}(t) =&f_{n-1}(x_1,\dots,x_{n-1})-\frac{a_n}{\beta_{1n}}\sum_{k=1}^{n-1}\beta_{1k}x_k -\frac{a_n}{\beta_{1n}}\phi_1(x_1,\dots,x_{n-1}).
\end{split}\qquad
(2.45)$$Обозначив $\beta_{1n}u_2=a_n\phi_1(x_1,\dots,x_{n-1})$, назовем $\phi_1$ внутренним управлением, которое переводит ИТ на второе
многообразие:
$$
\psi_2=\sum_{k=1}^{n-1}\beta_{2k}x_k +\phi_2(x_1,\dots,x_{n-2})=0. \qquad
(2.46)$$Размерность $\psi_2=0$ (2.46) на единицу меньше размерности многообразия $\psi_1=0$. Управление $u_2(x_1,\dots,x_{n-1})$ подобъектом (2.45), синтезируемое на основе агрегированной переменной $\psi_2$, имеет вид
$$
\begin{split}
u_2 = &\frac 1{\beta_{2,n-1}} \sum_{i=1}^p \left( \beta_{2i} + \frac{\partial \phi_2}{\partial x_i} \right) f_i + \frac 1{\beta_{2,n-1}} \sum_{j=p+1}^{n-2} \left( \beta_{2i} + \frac{\partial \phi_2}{\partial x_i} \right)\times\\
&\times (f_j + a_{j+1}x_{j+1} )- \frac{a_n}{\beta_{1n}}\sum_{k=1}^{n-1}\beta_{1k}x_k + \frac 1{\beta_{2,n-1}T^2}\psi_2 + f_{n-1}.
\end{split}\qquad
(2.47)$$

Управление $u_2$ (2.47) обеспечивает перевод ИТ в окрестность многообразия (2.46), движение вдоль которого описывается системой дифференциальных
уравнений
$$
\begin{split}
\dot x_1(t) &=f_i(x_1,\dots,x_n), \quad i=1,2,\dots,p;\\
\dot x_j(t) &=f_j(x_1,\dots,x_j) +a_{j+1}x_{j+1}, \quad j=p+1,\dots,n-2;\\
\dots\dots & \dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots;\\
\dot x_{n-2}(t) &=f_{n-2}(x_1,\dots,x_{n-2})-\frac{a_{n-1}}{\beta_{2,n-1}}\sum_{k=1}^{n-2}\beta_{2k}x_k -\frac{a_{n-1}}{\beta_{2,n-1}}\phi_2(x_1,\dots,x_{n-2}).
\end{split}
$$Обозначив $\beta_{2,n-1}u_3=a_{n-1}\phi_2(x_1,\dots,x_{n-2})$, можно, в свою очередь, найти управление $u_3(x_1,\dots,x_{n-2})$, обеспечивающее перевод ИТ в окрестность многообразия:
$$
\psi_3=\sum_{k=1}^{n-2}\beta_{3k}x_k +\phi_3(x_1,\dots,x_{n-3})=0.
$$Аналогично, в общем случае можно осуществить последовательный перевод изображающей точки в окрестности многообразий $\psi_4=0$, $\psi_5=0$ и т.д., вплоть до некоторогомногообразия $\psi_l=0$. При этом последовательность внутренних управлений определяется выражениями:
$$
\begin{split}
u_l&(x_1,\dots,x_{n-l+1})=\frac{a_{n-l+1}}{\beta_{l-1,n-l+2}}\phi_{l-1}(x_1,\dots,x_{n-l+1}),\quad l=1,2,\dots,r;\\
u_l&=\frac 1{\beta_{l,n-l+1}} \sum_{i=1}^p \left( \beta_{li} + \frac{\partial \phi_l}{\partial x_i} \right) f_i + f_{n-l+1} + \frac 1{\beta_{l,n-l+1}} \sum_{j=p+1}^{n-l} \left( \beta_{li} + \frac{\partial \phi_l}{\partial x_i} \right) \times\\
&\times(f_j+a_{j+1}x_{j+1}) - \frac{a_{n-l+2}}{\beta_{l-1,n-l+2}}\sum_{k=1}^{n-l+1}\beta_{l-1,k}x_k + \frac 1{T_l\beta_{l,n-l+1}}\psi_l.
\end{split}\qquad(2.48)$$Движение ИТ вдоль соответствующих многообразий
$$
\psi_l=\sum_{k=1}^{n-l+1}\beta_{lk}x_k + \phi_l(x_1,\dots,x_{n-l})=0
(2.49)$$описывается системами дифференциальных уравнений
$$
\begin{split}
\dot x_i(t) &=f_i(x_1,\dots,x_n), \qquad\qquad\qquad\; i=1,2,\dots,p;\\
\dot x_j(t) &=f_j(x_1,\dots,x_j) + a_{j+1}x_{j+1}, \quad j=p+1,p+2,\dots,n-l+1;\\
\dots\dots &\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots;\\
\dot x_{n-l}(t) &=f_{n-l}(x_1,\dots,x_{n-l}) -\frac{a_{n-l+1}}{\beta_{l,n-l+2}}\sum_{k=1}^{n-l}\beta_{lk}x_k - \\
&-\frac{a_{n-l+1}}{\beta_{l,n-l+2}}\phi_l(x_1,\dots,x_{n-l}),\quad\;
l=1,2,\dots,r, \quad r\le n-1.
\end{split}\qquad
(2.50)$$В соответствии с изложенной процедурой управление $u_1(x_1,\dots,x_n)$ (2.44) переводит ИТ сначала в окрестность многообразия, затем внутренние управления (2.48) последовательно переводят ее в окрестность многообразий $\psi_l=0$ (2.49), ($l=2,\dots,r$), движения вдоль которых описываются системами дифференциальных уравнений вида (2.50). Управления $u_l(x_1,\dots,x_{n-l+1})$ (2.48) синтезировались на каждом этапе на основе функциональных уравнений
$$
T_l\dot\psi_l(t) + \psi_l=0, \quad l=1,2.\qquad
(2.51)$$Законы управления $u_l$ (2.48) обеспечивают перевод ИТ с $i$-го на \mbox{($i+1$)-е} многообразие, движение вдоль которых описываются уравнениями вида (2.50). Из выражений для $\psi_1,\dots,\psi_r$ (2.49) видно, что размерность $i$-го многообразия на единицу меньше размерности ($i-1$)-го многообразия. Указанное последовательное понижение размерности фазового пространства при движении ИТ вдоль соответствующих многообразий $\psi_i=0$ аналогично протеканию оптимальных по быстродействию процессов, для которых характерной особенностью является последовательное понижение размерности гиперповерхностей переключения. Следовательно, введение некоторой последовательности притягивающих многообразий $\psi_i=0$ позволяет ускорить время протекания переходных процессов. Процедура синтеза в соответствии с предложенным здесь методом состоит в формировании закона управления $u_1(x_1,\dots,x_n)$ (2.44).
При этом основной задачей является определение функции $\phi_1(x_1,\dots,x_{n-1})$ и ее ($n-1$) производных $\dfrac{\partial \phi_1}{\partial x_j}$. Функция $\phi_1(x_1,\dots,x_{n-1})$ может быть найдена в результате последовательного определения вспомогательных функций $\phi_2(x_1,\dots,x_{n-2}),\dots,\phi_r(x_1,\dots,x_{n-r})$, входящих в соответствующие внутренние управления $u_l(x_1,\dots,x_{n-l+1})$
(2.48). Конкретно эта задача решается в обратной последовательности: сначала выбирается функция $\phi_r(x_1,\dots,x_{n-r})$, исходя из условий асимптотической устойчивости и требований к качеству движения на заключительном $r$-м этапе; затем находится функция $\phi_{r-1}(x_1,\dots,x_{n-r+1})$, после этого функция $\phi_{r-2}(x_1,\dots,x_{n-r+2})$ и т.д., вплоть до функции, которая позволяет непосредственно завершить процедуру синтеза закона управления $u_l(x_1,\dots,x_{n-l+1})$ (2.48). Для реализации указанной последовательности определения функции и вычисления внутренних управлений $u_l$ движением вдоль соответствующих многообразий $\psi_l=0$ выше приведены все необходимые соотношения (2.44)—(2.51). На их основе можно найти соответствующие конкретные выражения для $u_l$, $\psi_l$ и $\phi_l$ и, в конечном итоге, синтезировать стабилизирующие законы управления. На завершающем этапе синтеза находится управление на основе агрегированной переменной
$$
\phi_r=\sum_{k=1}^{n-r+1}\beta_{rk}x_k +\phi_r(x_1,\dots,x_{n-r}).
$$Выбрав должным образом функцию $\phi_r(x_1,\dots,x_{n-r})$ и коэффициенты $\beta_i$, можно закончить решение задачи синтеза нелинейной системы.

Изложенный подход к синтезу нелинейных систем, основанный на введении в фазовом пространстве совокупности притягивающих многообразий, в полной мере соответствует последовательной оптимизации систем, т.к. ИТ сначала попадет из внешней области на 1-е многообразие, затем на 2-е и т.д., вплоть до $r$-го. При этом движение вдоль каждого $i$-го многообразия является асимптотически устойчивым в целом. Таким образом, осуществляется последовательная оптимизация движения в процессе попадания ИТ на конечное многообразие в фазовом пространстве.

Для систем, синтезируемых на основе изложенного здесь метода введения последовательности притягивающих многообразий, можно выявить ряд общих закономерностей в отношении их динамических свойств и показателей качества.

Рассмотрим, например, возможности получения оценок времени затухания переходных процессов. Время регулирования в рассматриваемых системах определяется суммой времен приближения ИТ к $r$ многообразиям и времени движения вдоль конечного многообразия $\psi_r=0$ к началу координат фазового пространства. При этом каждое парциальное движение удовлетворяет уравнениям
$$
T_l\dot\psi_l(t) + \psi_l=0, \quad l=1,2,\dots \;.\qquad
(2.52)$$Тогда, согласно (2.52), оценка для суммарного времени регулирования будет иметь вид
$$
t_{\Sigma p}\le (4\dots 5)\sum_{l=1}^{r-1}T_l + t_{\psi r},\qquad
(2.53)$$где $t_{\psi r}$ — время движения вдоль финишного многообразия $\psi_r=0$ к началу координат декомпозированной подсистемы.

Таким образом, предложенный метод АКАР, основанный на введении в фазовом пространстве последовательности притягивающих многообразий, позволяет гарантировать асимптотическую устойчивость невозмущенного движения синтезируемых систем, т.е. решить задачу стабилизации нелинейных систем, обеспечить требуемое время затухания переходных процессов и т.д.

Предложенный метод синтеза по своему существу базируется на декомпозиции исходной задачи $n$-го порядка на $r$ подзадач последовательно понижающейся размерности и на подзадачу ($n-r$)-го порядка. При этом декомпозиция общего движения в исходном фазовом пространстве на парциальные движения основывается не на некоторых приближенных свойствах рассматриваемых объектов (связанных, например, с разнотемповостью движений из-за больших отличий постоянных времени), а на последовательном во времени переводе ИТ с одного многообразия на следующее меньшей размерности. Другими словами, происходит поинтервальное разделение движений, когда в результате сближения ИТ со следующим многообразием меньшей размерности парциальные движения как бы “выстраиваются” в очередь друг за другом. Указанные отличия предложенного здесь метода и позволяют осуществить не приближенную, а точную динамическую декомпозицию основного движения системы.

2.6.2. Примеры аналитического конструирования скалярных регуляторов для нелинейных динамических объектов

Рассмотрим сначала особенности метода АКАР при решении задач синтеза систем скалярного управления объектами с различными нелинейностями.

Пример 1.

Предположим, что объект описывается дифференциальными уравнениями
$$
\dot x_1(t)=ax_1^3 +x_2; \quad \dot x_2(t)=u.\qquad
(2.54)$$Особенностью объекта (2.54) при $a>0$ является его существенная неустойчивость, т.к. при $x_2(t)\to 0$ координата $x_1(t)\to\infty$, что накладывает дополнительные требования к синтезируемым законам управления $u(x_1,x_2)$, которые должны обеспечивать стабилизацию ($x_1\to 0$, $x_2\to 0$) системы при произвольных начальных условиях. Применим метод АКАР для синтеза таких законов управления. Для этого выберем функцию $\psi$ сначала в виде
$$
\psi_1=x_2 +\beta x_1 +b x_1^3.\qquad
(2.55)$$Подставляя (2.55) в уравнение
$$
T_1\dot\psi_1 +\phi(\psi_1)=0,
$$получаем следующее общее выражение:
$$
u_1(x_1,x_2)=-\big(3bx_1^2 +\beta\big)\big(ax_1^3 +x_2\big) -\frac 1{T_1}\phi(\psi_1), \quad T_1>0,\qquad
(2.56)$$которое в зависимости от выбранной функции $\phi(\psi_1)$ позволяет получить различные законы управления. Эти законы обеспечивают асимптотически устойчивое движение ИТ в окрестность многообразия $\psi_1=0$ (2.55), т.к. функция $\phi(\psi_1)$ выбирается такой, чтобы $\phi(\psi_1)\cdot \psi_1>0$. Дифференциальное уравнение, описывающее движение вдоль $\psi_1=0$, имеет вид
$$
\dot x_{|\psi|}(t)=-\beta x_{|\psi|}-(b-a)x_{|\psi|}^3.\qquad
(2.57)$$Для оценки устойчивости уравнения (2.57) используем функцию Ляпунова $\mathrm V=0,5 x_{|\psi|}^2$, тогда ее производная по времени, взятая в силу уравнения (2.57), будет равна
$$
\dot {\mathrm V}(t)=-\beta x_{|\psi|}^2 -(b-a)x_{|\psi|}^4<0.
$$Отсюда следует, что неравенства $\beta>0$, $b\ge a$, $T_1>0$ являются условиями асимптотической устойчивости в целом синтезированной замкнутой системы (2.54), (2.56):
$$
\dot x_1(t)=ax_1^3 =x_2;\quad \dot x_2(t)=-\big(3bx_1^2 +\beta\big)\big(ax_1^3 +x_2\big) -\frac 1{T_1}\phi(\psi_1).\qquad
(2.58)$$Определим первые интегралы системы (2.58), для чего представим ее в следующей симметричной форме:
$$
\frac{dx_1}{ax_1^3 +x_2}=-\frac{T_1dx_2}{T_1\big(3bx_1^2 +\beta\big)\big(ax_1^3 +x_2\big) +\phi(\psi_1)}=dt.\qquad
(2.59)$$

Положив в (2.59) функцию $\psi_1=0$ и, следовательно, $\phi(0)=0$, после интегрирования находим первый интеграл $ax_1 +bx_1^3 =-x_2$, который совпадает с выражением $\psi_1=0$ (2.55). Другими словами, мы убедились в том, что заданное инвариантное многообразие $\psi_1=0$ (2.55} действительно является претендентом на желаемое притягивающее многообразие синтезированной нелинейной системы.

При $\phi=\psi_1=x_2 +\beta x_1 +ax_1^3$ закон управления (2.56) принимает вид
$$
u_1 =-\frac{\beta}{T_1}x_1 -\frac 1{T_1}x_2 -\frac{a}{T_1}x_1^3 -\big(3ax_1^2 +\beta\big)\big(x_1^3 +x_2\big).\qquad
(2.60)$$

На рис. 2.8 для этого закона и параметров $\beta=1$, $a=1$, $T_1=1$ изображены траектории движения замкнутой системы. Как видно из рис. 2.8, фазовые траектории “наматываются” на многообразие $\psi_1=0$ (2.55), стягиваясь к нему в начале координат. При этом система является асимптотически устойчивой с апериодическим характером затухания переходных процессов.

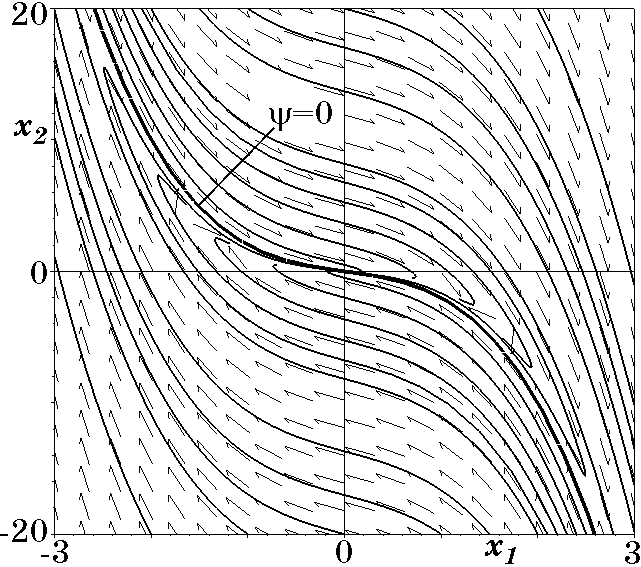
Рис. 2.8. Фазовый портрет системы

Предположим теперь, что на координату $x_2$ наложено ограничение $|x_2|\le A$. Тогда, введя функцию

$$
\psi_2=x_2 + A\tanh(\beta x_1 + \beta x_1^3),\qquad
(2.61)$$получаем выражение для закона управления
$$
u_2=-\frac{A\big(\beta + 3bx_1^2\big)\big(a x_1^3 + x_2\big)}{ch^2\big(\beta x_1 + b x_1^3\big)} -\frac 1{T_2}\phi(\psi_2), \quad T_2>0,\qquad
(2.62)$$который переводит ИТ в окрестность многообразия $\psi_2=0$ (2.61) и обеспечивает в зависимости от выбранной функции $\phi(\psi_2)$ и параметров $\beta$ и $a$ соответствующее качество переходных процессов. Уравнение движения вдоль многообразия $\psi_2=0$ имеет вид
$$
\dot x_{1\psi 2}(t) =x_{1\psi 2}^3 -A\tanh\big(\beta x_{1\psi 2} + b x_{1\psi 2}^3\big).\qquad
(2.63)$$

Из уравнения движения (2.63) следует, что условия $\beta>0$, $b\ge 1$ обеспечивают его асимптотическую устойчивость только в определенной области. Это означает, что введение ограничения $|x_2|\le A$ и, следовательно, функции $\psi_2$ (2.61) сужает область асимптотической устойчивости замкнутой системы (2.54), (2.62). На рис. 2.9, рис. 2.10 и рис. 2.11 соответственно для функций $\phi=\psi_2$, $\phi=\tanh\psi_2$, и $\phi=\mathrm{sign}\psi_2$ и параметров $b=1$, $T=1$, $A=1$ изображены траектории движения, которые подтверждают наличие области асимптотической устойчивости с апериодическими переходными процессами в синтезированной системе.

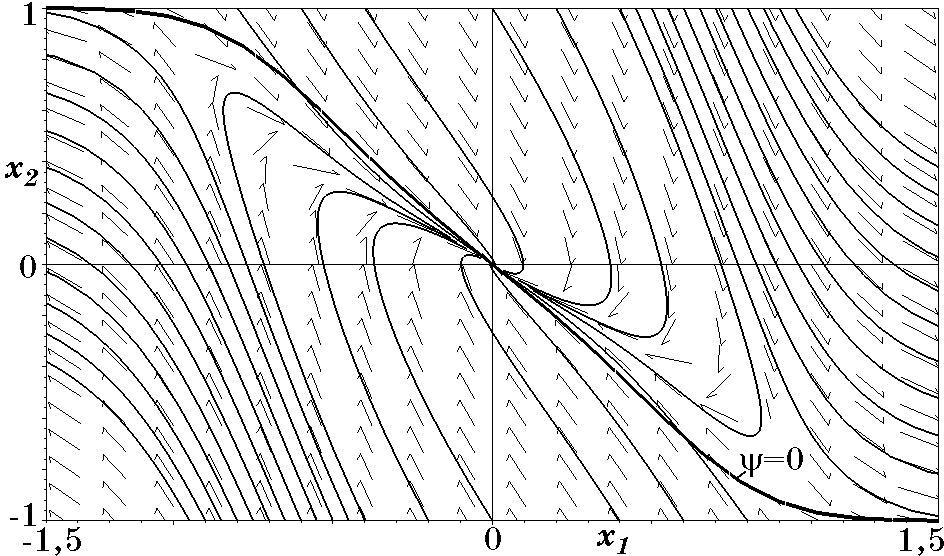
Рис. 2.9. Фазовый портрет системы при $\phi=\psi_2$

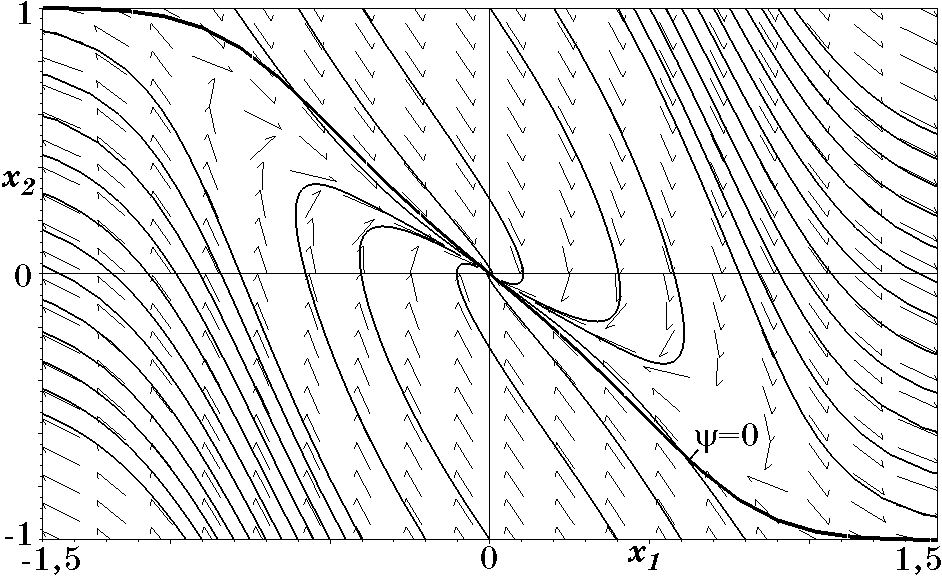
Рис. 2.10. Фазовый портрет системы при $\phi=\tanh\psi_2$

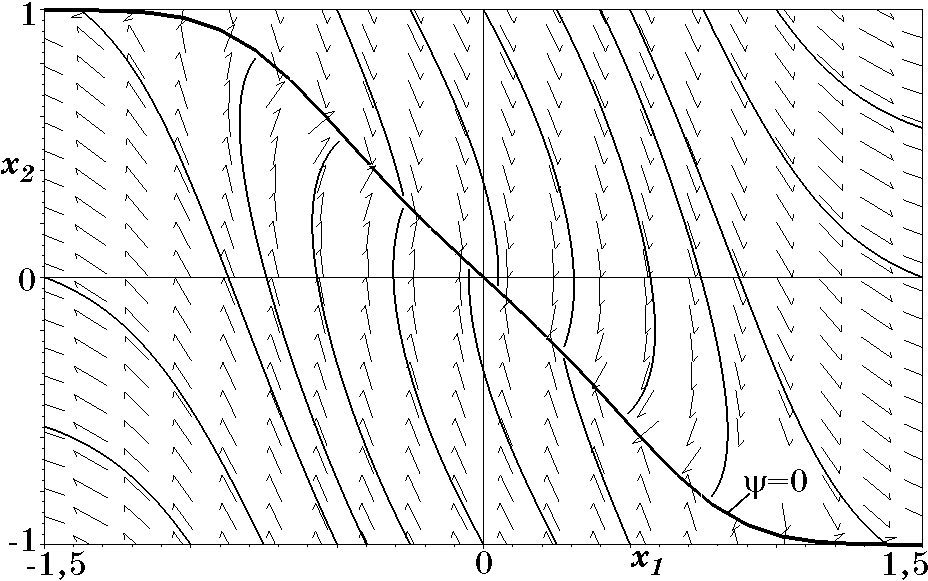
Рис. 2.11. Фазовый портрет системы при $\phi=\mathrm{sign}\psi_2$

В режиме малых отклонений, когда $\psi_{2\inf}=x_2 + A\beta x_1$, законы управления $u_2$ (2.62) и $u_1$ (2.56) ($A=1$) будут оптимальными по квадратичному критерию
$$
J_{\inf}=\int\limits_0^x\Big[\beta^2A^2x_1^2 +\big(1+\beta^2 A^2 T^2\big)x_2^2 + T^2 u^2\Big]dt.\qquad
(2.64)$$Выбор весовых коэффициентов в критерии (2.64) зависит от желаемых показателей качества переходных процессов. Итак, синтезированные методом АКАР законы управления $u_1$ (2.56) и $u_2$ (2.62) гарантируют асимптотическую устойчивость соответственно в целом или в области $|x_2|\le A$ и обеспечивают требуемые свойства замкнутой системе.

•

Пример 2

Синтезируем закон управления объектом
$$
\dot x_1(t) =x_1^2 +x_2, \quad \dot x_2(t)=u,\qquad
(2.65)$$имеющим экстремальную нелинейность. Введя функцию
$$
\psi =x_2 +\beta x_1 +ax_1|x_1|\qquad
(2.66)$$и подставив ее в функциональное уравнение
$$
T_1\dot \psi(t) +\psi =0,
$$в силу уравнений объекта (2.65) найдем следующий закон управления:
$$
u=-\frac{\beta}{T}x_1 -\frac a T x_1|x_1|-\frac 1T x_2 -\big(2a|x_1| + \beta\big)\big(x_2^2 + x_2\big).% \vspace{-1mm}\qquad
(2.67)$$Закон (2.67) переводит ИТ в окрестность многообразия $\psi=0$ (2.66), движение вдоль которого описывается дифференциальным уравнением
$$
\dot x_{1\psi}(t) = x_{1\psi}^2 -\beta x_{1\psi} -a|x_{1\psi}|x_{1\psi}.
$$Исследуем устойчивость последнего уравнения относительно $x_{1\psi}=0$ Для этого введем функцию Ляпунова $\mathrm V=0,5x_{1\psi}^2$ и определим ее производную:
$$\dot{\mathrm V}(t)=x_{1\psi}^3 -\beta x_{1\psi}^2 -a|x_{1\psi}|x_{1\psi}^2.
$$Очевидно, что для $x_{1\psi}<0$ производная $\dot{\mathrm V}(t)<0$ при $\beta>0$, $a>0$, а для $ x_{1\psi}>0$ производная $\dot{\mathrm V}(t)<0$ при $\beta>0$, $a\ge 1$. Это означает, что при $\beta>0$, $a\ge 1$ это уравнение и, следовательно, синтезируемая система обладают свойством асимптотической устойчивости в целом относительно состояния $x_1=x_2=0$. На рис. 2.12 приведены траектории движения замкнутой системы при $\beta=1$, $T=1$, $a=2$. Заметное отличие рис. 2.12 от аналогичных фазовых портретов систем второго порядка состоит в поведении траекторий в третьем квадранте. Обычно законы управления представляют собой некоторое многообразие, проходящее через второй и четвертый квадранты фазовой плоскости.

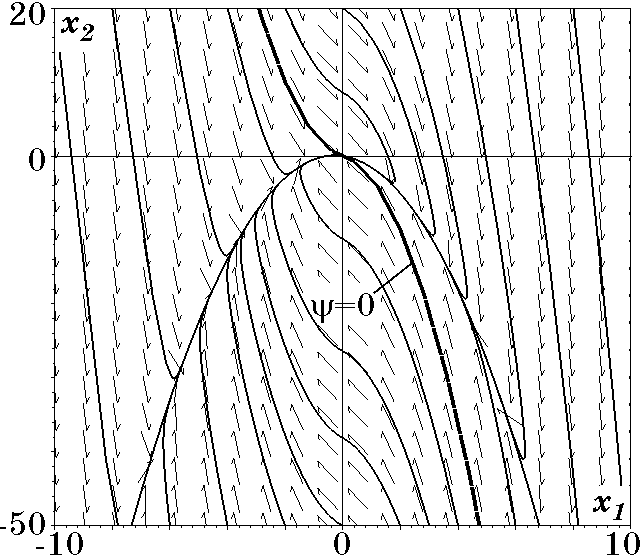
Рис. 2.12. Фазовый портрет системы

•

Пример 3

Рассмотрим задачу аналитического конструирования системы управления движением центра масс подвижного объекта, поведение которого описывается системой дифференциальных уравнений [69]:
$$
m\Delta \ddot h(t)=a_1\delta + b_1\delta^3; \quad T\dot\delta(t) + \delta =c_1u,\qquad
(2.68)$$где $\Delta h$ — координата центра масс, $\delta$ — отклонение управляющего органа, $m$, $a_1$, $b_1$, $c_1$ $T$ — постоянные коэффициенты. Запишем уравнения (2.68) в форме
$$
\dot x_1(t)=x_2; \quad \dot x_2(t)=ax_3 +b x_3^3; \quad \dot x_3(t)=-\omega x_3 +c u,\qquad
(2.69)$$где $x_1=\Delta h$, $x_2=\Delta\dot h(t)$, $x_3=\delta$, $a=\dfrac{a_1}{m}$, $b=\dfrac{b_1}{m}$, $\omega =\dfrac 1T$, $c=\dfrac{c_1}T$. Требуется найти закон управления $u(x_1,x_2,x_3)$, обеспечивающий перевод объекта (2.69) из произвольной точки пространства состояний в точку равновесия $x_k(0,0,0)$, при этом должны обеспечиваться определенные требования к динамическим свойствам системы, выражаемые, например, в форме минимизации некоторого квадратичного критерия качества.

Применим сначала метод АКАР для объекта (2.69), представленного дифференциальными уравнениями в канонической форме:
$$
\dot y_1(t)=y_2; \quad \dot y_2(t)=y_2; \quad \dot y_3(t)=u_0,\qquad
(2.70)$$где $y_1=x_1$, $y_2=x_2$, $y_3=\dot x_2(t)=ax_3 +b x_3^3$, $u_0=\big(a+3bx_3^2\big)(-\omega x_3 +cu_1)$.

Выберем следующую линейную макропеременную:
$$
\psi_1=\rho_1y_1 +\rho_2y_2 +y_3.\qquad
(2.71)$$Тогда, подставляя $\psi_1$ (2.70) в функциональное уравнение
$$
T_1\dot\psi_1(t) +\psi_1=0,\qquad
(2.72)$$в силу уравнений объекта (2.70) получаем закон управления
$$
u_0=-\frac{\rho_1}{T_1}y_1 -\left(\rho_1 +\frac{\rho_2}{T_1}\right)y_2 -\left(\rho_2 +\frac{1}{T_1}\right)y_3.\qquad
(2.73)$$Переходя к исходным координатам, имеем
$$
cu_1 =-\frac{1}{\big(a+3bx_3^2\big)}\Bigg[\frac{\rho_1}{T_1}x_1 + \left(\rho_1 +\frac{\rho_2}{T_1}\right)x_2 %+\\
+\left(\rho_2 +\frac{1}{T_1}\right)\big(a +b x_3^2\big)x_3\Bigg] +\omega x_3.\qquad
(2.74)$$Рассмотрим свойства синтезированной системы с позиций метода АКАР. Закон управления $u_0$ (2.73) переводит ИТ объекта из произвольного начального состояния в окрестность многообразия
$$
\psi_1=\rho_1y_1 +\rho_2y_2 +y_3=0,\qquad
(2.75)$$движение вдоль которого описывается следующей системой дифференциальных уравнений:
$$
\dot y_{1\psi 1}(t)=y_{2\psi 1}, \quad \dot y_{2\psi 1}(t)=-\rho_1y_{1\psi 1}-\rho_2y_{2\psi 1}.\qquad
(2.76)$$Условия асимптотической устойчивости в целом уравнений (2.76) и, следовательно, синтезированной замкнутой системы (2.69), (2.74) будут иметь форму простых неравенств:
$$
\rho_1>0; \quad \rho_2>0; \quad T_1>0.
$$Результаты моделирования замкнутой системы управления объектом (2.69) с регулятором (2.74) представлены на рис. 2.13 и рис. 2.14.

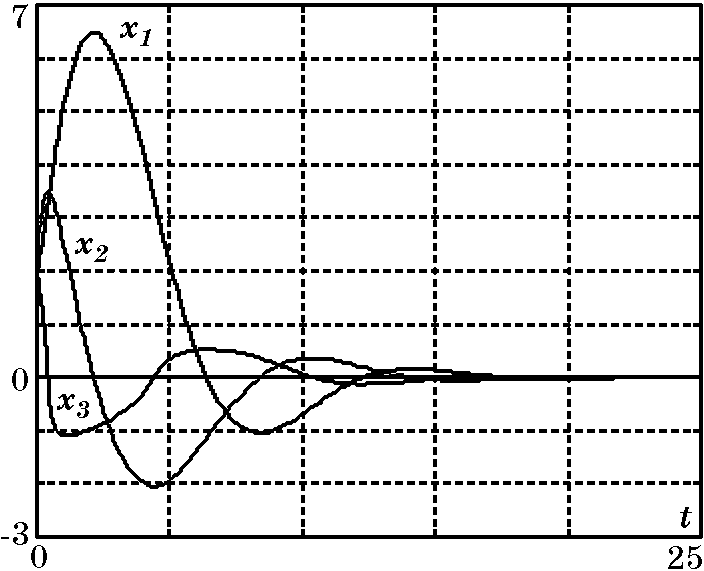
Рис. 2.13. Графики переходных процессов

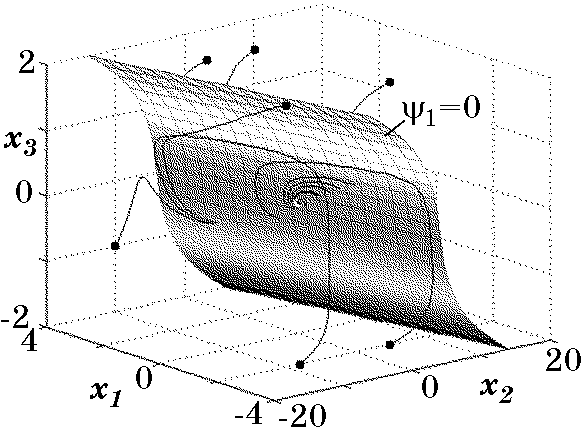
Рис. 2.14. Фазовый портрет системы}

•

Перейдем далее к рассмотрению возможностей синтеза других законов управления объектом (2.69) с использованием метода АКАР. Структура этих законов зависит от формы выбираемого инвариантного многообразия и вида функционального уравнения. В связи с этим введем в рассмотрение следующую макропеременную:
$$
\psi_2 =x_3 + \phi(x_1,x_2)\qquad
(2.77)$$и функциональное уравнение
$$
T_2\dot \psi_2(t) +F(\psi_2)=0,\qquad
(2.78)$$где $F(\psi_2)\psi_2>0$. В соответствии с методом АКАР синтезируемые законы управления $u_2(x_1,x_2,x_3)$ обеспечивают перевод ИТ объекта в окрестность многообразия $\psi_2=0$ (2.77), движение вдоль которого описывается согласно (2.69) следующей системой дифференциальных уравнений:
$$
\dot x_{1\psi 2}(t)=x_{2\psi 2}; \quad \dot x_{2\psi 2}(t)=-a\phi\big(x_{1\psi 2},x_{2\psi 2}\big) -b\phi^3\big(x_{1\psi 2},x_{2\psi 2}\big).\qquad
(2.79)$$Соответствующим синтезом внутреннего управления $\phi(x_1,x_2)$ можно обеспечить требуемые динамические свойства при движении вдоль многообразия $\psi_2=0$ (2.77). Подставив $\psi_2=0$ в (2.78), в силу уравнений объекта (2.69) найдем выражение
$$
c u_2=-\frac{\partial \phi}{\partial x_1} x_2 -\frac{\partial \phi}{\partial x_2}\big(a + bx_3^2\big) x_3 -\frac{1}{T_2}F(\psi_2) +\omega x_3,\qquad
(2.80)$$охватывающее определенную совокупность допустимых законов управления. Выберем сначала простую линейную функцию
$$
\phi(x_1,x_2)=\beta_1 x_1 + \beta_2 x_2.\qquad
(2.81)$$Тогда, подставив выражение (2.81) в (2.80), с учетом $\psi_2$ (2.77), получим следующий закон управления при $F(\psi_2)=\psi_2$:
$$
c u_2=-\frac{\beta_1}{T_2} x_1 -\left( \beta_1 +\frac{\beta_2}{T_2}\right )x_2 -\left( \beta_2 a +\beta_2 b x_3^2 + \frac {1}{T_2} -\omega\right) x_3,\qquad
(2.82)$$при этом уравнения (2.79) будут иметь вид
$$
\dot x_{1\psi 2}(t)=x_{2\psi 2}; \quad \dot x_{2\psi 2}(t)=-\beta_1 a x_{1\psi 2} - \beta_2 a x_{2\psi 2} - b\big( \beta_1 x_{1\psi 2} + \beta_{2\psi 2}\big)^3.\qquad
(2.83)$$Условия асимптотической устойчивости в целом для уравнений (2.83) и, следовательно, для замкнутой системы (2.69), (2.82) принимают форму простых неравенств
$$
\beta_1>0; \quad \beta_2>0; \quad T_2>0.\qquad
(2.84)$$Закон управления $u_2$ (2.82) при выполнении неравенств (2.84) обеспечивает асимптотически устойчивое движение ИТ вдоль многообразия $\psi_2=0$ (2.77), он проще закона $u_1$ (2.74). Это объясняется тем, что здесь использовались исходные уравнения объекта (2.69), а синтез закона $u_2$ (2.82) основывался на выборе соответствующего внутреннего управления $\phi(x_1,x_2)$ (2.81) для обеспечения желаемых свойств движения вдоль многообразия $\psi_2=0$ (2.77), определяемого дифференциальными уравнениями (2.83). Параметры $\beta_1$, $\beta_2$ и $T_2$ закона $u_2$ (2.82) должны удовлетворять условиям (2.84) и могут быть, в частности, определены исходя из желаемых динамических свойств замкнутой системы в режиме малых отклонений от заданного состояния. Результаты моделирования замкнутой системы с законом управления $u_2$ (2.82) представлены на рис. 2.15 и рис. 2.16.

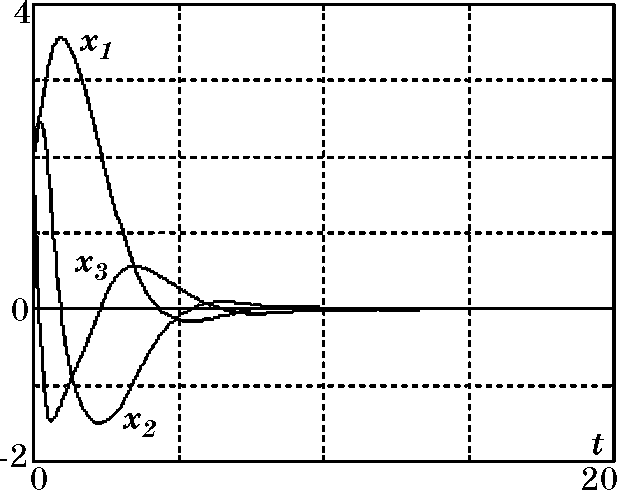
Рис. 2.15. Графики переходных процессов

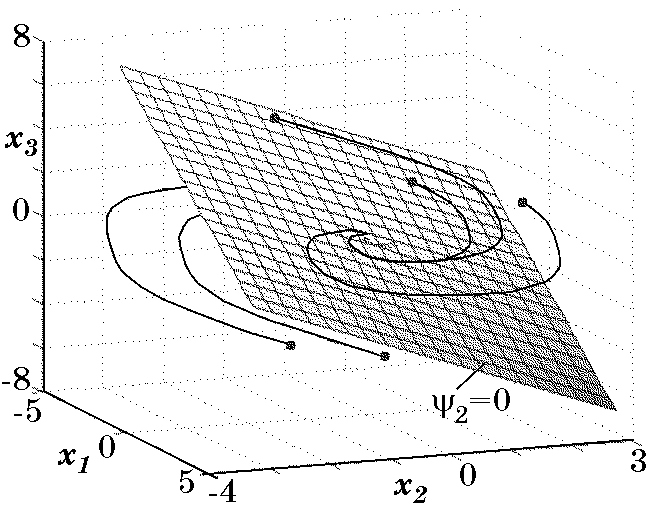
Рис. 2.16. Фазовый портрет системы

Для повышения быстродействия при движении ИТ вдоль многообразия $\psi_2=0$ (2.77) можно ввести нелинейную функцию
$$
\phi(x_1,x_2)=\beta_1x_1 +\beta_2x_2 +\beta_3x_2^3.
$$Тогда закон (2.80) при $F(\psi_2)=\psi_2$ принимает вид
$$
cu_2=-\beta_1x_2 -\big( \beta_2 + 3\beta_3x_2^2\big)\big(a +b x_3^2\big)x_3 -\frac{1}{T_2}\psi_2 +\omega x_3.\qquad
(2.85)$$Выбирая другие функции $\phi(x_1,x_2)$ и $F(\psi_2)$, можно аналогично (2.82), (2.85) получить соответствующие законы управления. Результаты моделирования замкнутой системы с законом управления $u_2$ (2.85) представлены на рис. 2.17 и рис. 2.18.

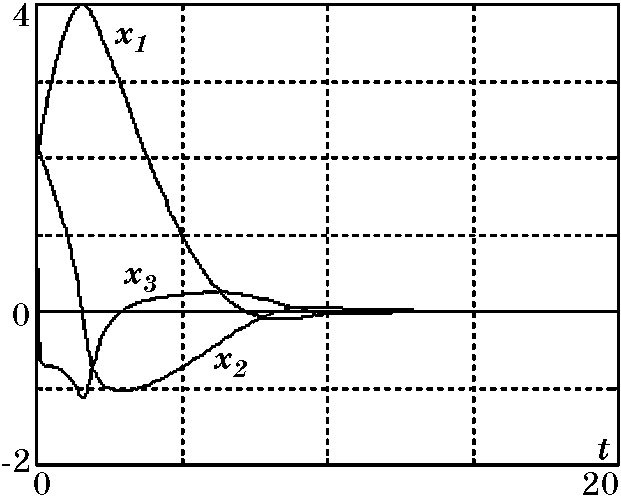
Рис. 2.17. Графики переходных процессов

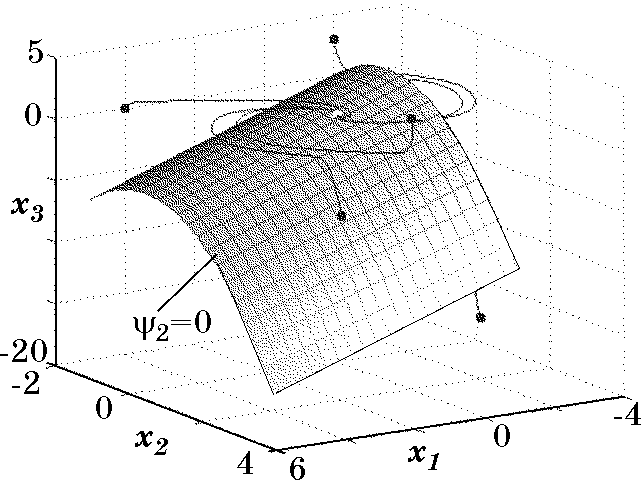
Рис. 2.18. Фазовый портрет системы

Предположим далее, что расход рабочего тела на управление ограничен, т.е. на скорость изменения центра масс наложено некоторое ограничение $|x_2|\le A/\beta_2$. Тогда для его учета можно использовать следующую макропеременную:
$$
\psi_2 =\beta_2 x_2 + A\tanh(x_3 +\beta_1x_1).
$$Подставляя $\psi_3$ в функциональное уравнение
$$
T_3\dot\psi_3(t) + \psi_3 =0,
$$в силу уравнений объекта (2.69) получаем закон управления
$$
cu_3 =\omega x_3 -\beta_1 x_2 -\frac 1A ch^2\big(x_3 +\beta_1 x_1\big)\left( \beta_2 a x_3 +\beta_2 b x_3^3 +\frac 1{T_3}\psi_3\right).\qquad
(2.86)$$Этот закон обеспечивает ограничение $|x_2|\le A$ и переводит ИТ из произвольного начального состояния объекта по координатам $x_1$ и $x_3$ в окрестность многообразия $\psi_3=0$, движение вдоль которого описывается системой дифференциальных уравнений:
$$
\begin{split}
\dot x_{1\psi3}(t) &=x_{2\psi3};\\
\dot x_{2\psi3}(t) &=-\beta_1x_{1\psi2} -a A r\tanh \frac{\beta_2}{A}x_{2\psi3} -b\left( \beta_1 x_{1\psi3} + A r\tanh \frac{\beta_2}{A}x_{2\psi3}\right)^3.
\end{split}
$$Условия устойчивости этих уравнений сводятся к неравенствам: $\beta_1>0$, $\beta_2>0$, которые определяют для замкнутой системы (2.69), (2.86) асимптотическую устойчивость движения по координате $x_2$ в области $|x_2|\le A/\beta_2$, а по координатам $x_1$, $x_3$ — в целом. Результаты моделирования замкнутой системы управления (2.69) с законом управления (2.86) представлены на рис. 2.19 и рис. 2.20.

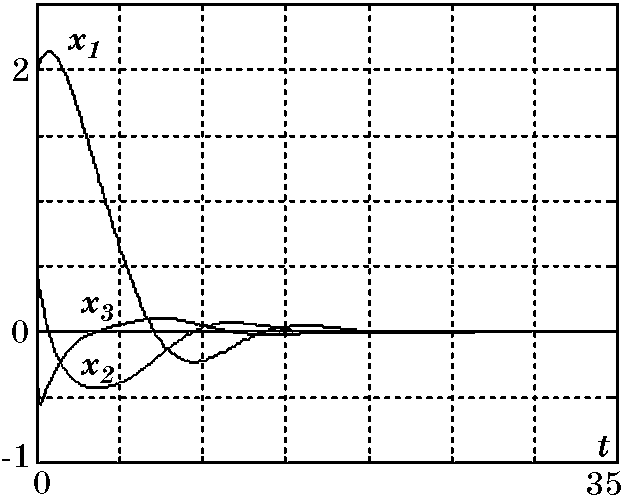
Рис. 2.19. Графики переходных процессов

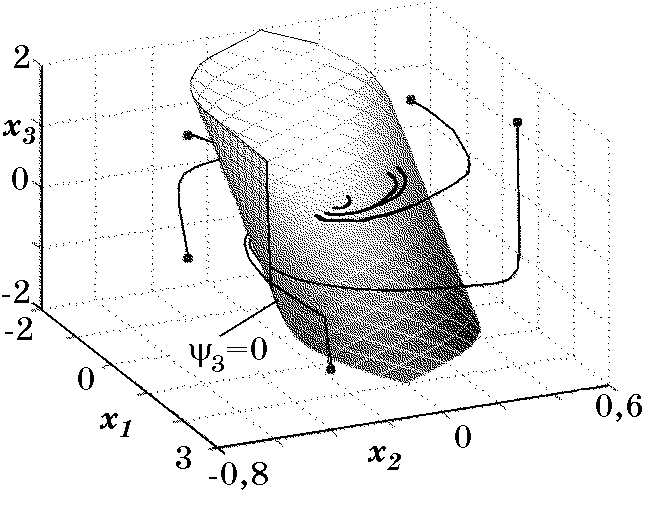
Рис. 2.20. Фазовый портрет системы

Изложенные выше подходы к задаче управления движением центра масс подвижного объекта (2.69) показывают достоинство метода АКАР, позволяющего в результате простых аналитических процедур получить совокупность законов управления, обеспечивающих желаемые требования к динамическим свойствам замкнутой системы. В монографии [61] приведены соответствующие критерии качества, по которым оптимизируются синтезированные законы управления.