Модуль 2. Общий метод аналитического конструирования нелинейных агрегированных регуляторов

2.2. Постановка задачи синтеза законов единства процессов самоорганизации и управления

Подчеркнем два фундаментальных свойства синергетических систем — это, во-первых, обязательный обмен с внешней средой энергией, веществом и информацией и, во-вторых, непременное взаимосодействие, т. е. когерентность поведения между компонентами системы. Представляется весьма перспективным для развития теории системного синтеза осуществить перенос свойств синергетических систем на конструируемые системы управления нелинейными объектами. Разумеется, что при этом возникает непростая проблема перехода от естественных синергетических принципов к количественным соотношениям. Такой подход позволил построить новую СТУ, имеющую глубокое естественно-научное обоснование как приложение принципов самоорганизации в проблемах управления. СТУ — это новое направление в общей теории управления, базирующееся на принципах направленной самоорганизации и динамической декомпозиции синтезируемых нелинейных систем на притягивающих инвариантных многообразиях (ИМ). Она отражает идеологию единства процессов самоорганизации и управления, т. е. представляет собой своего рода симбиоз кибернетики и синергетики. Основные особенности СТУ применительно к проблеме системного синтеза состоят, во-первых, в кардинальном изменении целей поведения синтезируемых систем; во-вторых, в непосредственном учете в процедурах синтеза естественных свойств нелинейных объектов; и, в-третьих, в формировании нового механизма генерации нелинейных обратных связей. Конкретно суть этих нововведений состоит в следующем:

• целью функционирования синтезируемых систем является достижение целевых аттракторов — асимптотических пределов в их пространстве состояний, отражающих желаемые технологические режимы систем;
• целевые аттракторы и ИМ отражают физическую сущность процессов, протекающих в соответствующем динамическом объекте. Указанные ИМ формируются на основе желаемых технологических (механических, энергетических и др.) инвариантов;
• введение ИМ в процедуру синтеза систем позволяет построить регулярный механизм аналитической генерации естественной совокупности отрицательных и положительных обратных связей, которые формируют процессы направленной самоорганизации.
  

Таким образом, при синергетическом подходе к синтезу систем целью их функционирования, в отличие от классической теории автоматического регулирования и теории оптимального управления, является не только выполнение требований к характеру переходного процесса, а, в первую очередь, обеспечение желаемого асимптотического поведения системы на аттракторе или в его близкой окрестности. Это связано с тем обстоятельством, что поведение любой нелинейной диссипативной системы может быть разделено на этап переходного движения, когда ее траектории устремляются к аттрактору, и этап асимптотического движения на желаемом аттракторе — цели системы. Такой подход позволяет принципиально разрешить проблему аналитического конструирования объективных законов управления нелинейными многомерными объектами. Это — законы обратных связей, синтезируемых на основе наиболее полных нелинейных моделей динамических объектов с непосредственным учетом их естественных закономерностей, физических критериев и ограничений.

Итак, в СТУ целью синтезируемой системы является достижение соответствующего желаемого аттрактора, размерность которого обычно существенно меньше размерности исходного пространства состояний системы (рис. 2.6). Отсюда вытекает идеология процессов обработки информации и управления в сложных нелинейных динамических системах: для этого необходимо, чтобы указанные процессы включали в себя, по меньшей мере, две фазы: во-первых, фазу расширения и, во-вторых, фазу сжатия пространства состояний. Эти фазы реализуются с помощью соответствующей совокупности обратных связей. При этом в фазе расширения в системе формируется подмножество различных альтернатив поведения для ее взаимодействия с внешней средой или другими системами. В фазе сжатия система преобразует область притяжения аттракторов, ранее построенных, в один из желаемых аттракторов — цель системы. Таким образом, СТУ базируется на языке инвариантов и аттракторов, который непривычен для известных методов теории управления. Этот язык, как основной элемент СТУ, позволяет установить непосредственную связь с законами сохранения, т.е. фундаментальными естественными свойствами объектов различной природы. Инварианты, самоорганизация, каскадный синтез — это базовые понятия концептуального лексикона СТУ, определяющие ее сущность, новизну и содержание.

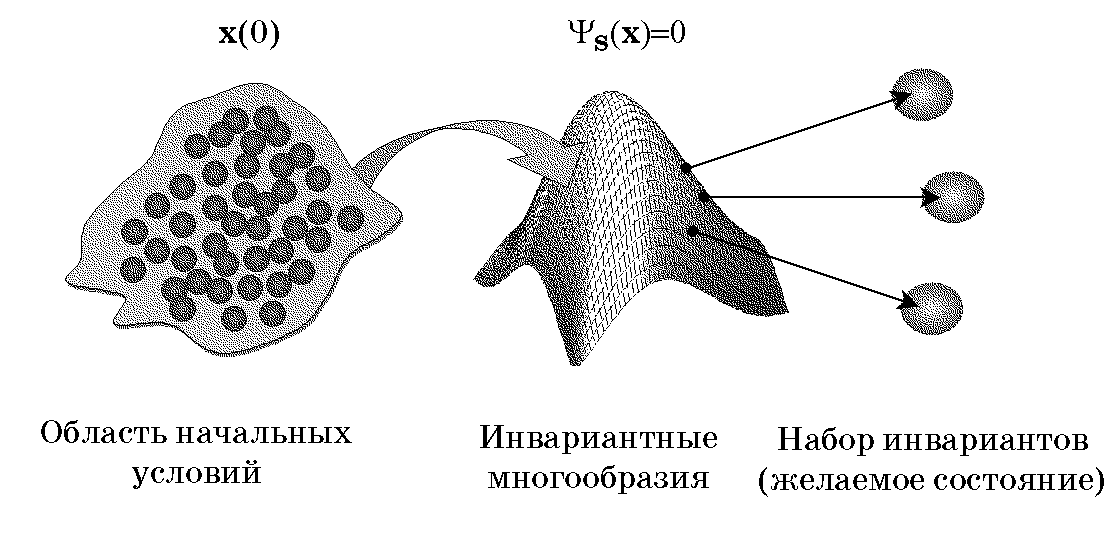
Рис. 2.6. Постановка проблемы синергетического синтеза систем

В СТУ формирование желаемых инвариантов и аттракторов позволяет осуществить способ направленной самоорганизации систем. В исходной постановке стандартной задачи управления система описывается дифференциальными уравнениями объекта:
$$
\dot{\mathbf x}(t)=\mathbf F\left(\mathbf{x,u,q,a,M}\right),\qquad
(2.16)$$в состав которых входят координаты состояния $\mathbf x(t)$, а также некоторые внешние силы, состоящие из искомых управлений $\mathbf u(t)$, задающих $\mathbf q(t)$, параметрических $\mathbf a(t)$ и внешних $\mathbf M(t)$ возмущающих воздействий. С целью перехода от схемы “объект— внешние силы” к формированию уравнений самоорганизации необходимо эти силы соответствующим образом исключить. Для этого следует расширить исходные уравнения системы “объект — внешние силы” (2.16) таким образом, чтобы включенные внешние силы оказались для нее внутренними. Тогда для новой, расширенной системы ее уравнения могут стать базовыми уравнениями формируемой самоорганизации, т.е. в результате указанного расширения можно перейти от организации системы к ее самоорганизации. Именно такого рода расширение происходит при соответствующей формулировке проблемы синтеза систем, которая состоит в определении законов управления в функции координат состояния расширенной системы. Эти законы, являющиеся уравнениями регулятора, должны обеспечить желаемые динамические свойства замкнутой системы “объект — закон управления”. Тогда по отношению к новой, расширенной системе целесообразно применить соотношения синергетики, характеризующие процессы направленной самоорганизации.

Другими словами, исходная система, состоящая из некоторого динамического объекта и действующих на него внешних сил, в результате замыкания прямыми и обратными связями преобразуется в новую, расширенную систему. При этом первоначальные воздействия, бывшие внешними силами по отношению к исходному объекту, становятся внутренними силами расширенной системы дифференциальных уравнений, в своей совокупности представляющих собой модель синергетического синтеза систем управления. Для такого преобразования следует в (2.16) представить задающие $\mathbf q(t)$, параметрические $\mathbf a(t)$ и внешние $\mathbf M(t)$ возмущающие воздействия как частные решения некоторых дополнительных дифференциальных уравнений, описывающих информационную модель, и тем самым осуществить их “погружение” в общую структуру расширенной системы размерности $\dim \Sigma$. Затем саму проблему управления необходимо уже формулировать как проблему поиска законов взаимодействия между компонентами расширенной системы, обеспечивающих возникновение в ней процессов самоорганизации. Конкретно эта проблема сводится к синтезу соответствующих законов управления $\mathbf u\left(x_1,\ldots,x_n,z_1,\ldots,z_r\right)$ в функции координат состояния расширенной системы. Здесь $z_1,\ldots,z_r$ — координаты информационных моделей задающих, внешних и параметрических возмущающих воздействий, записанных в виде дополнительных дифференциальных уравнений:
$$
\dot{\mathbf z}(t)=\boldsymbol\phi(\mathbf{x,z}),\qquad
(2.17)$$где $\mathbf z$ — оценки соответствующих возмущающих воздействий.

Уравнения (2.16) и (2.17) в совокупности и образуют модель синергетического синтеза систем управления. Тогда путем подведения энергии или вещества в такой расширенной системе (2.16) и (2.17) можно создать неравновесную ситуацию, необходимую для возникновения направленных процессов самоорганизации. Именно указанное расширение исходной системы и формирование уравнений самоорганизации позволяет установить связь между идеями синергетики и проблемой синтеза нелинейных систем на основе инвариантных соотношений. Отсюда следует, что СТУ — это, прежде всего, теория синтеза законов замкнутого управления на основе формирования самосогласованных, кооперативных процессов в системах различной природы. В соответствии с принципом “расширения— сжатия” (рис. 2.7) к базовым положениям синергетического подхода к проблеме синтеза нелинейных динамических систем относятся:

• во-первых, формирование расширенной системы дифференциальных уравнений, отражающих процессы отработки задающих воздействий, подавления возмущений, оптимизации, наблюдения координат и т.д.;
• во-вторых, формирование “внешних” управлений, которые обеспечивают редукцию избыточных степеней свободы системы по отношению к финишному ИМ, движение вдоль которого описывается уравнениями “внутренней” динамики декомпозированной системы;
• в-третьих, формирование между “внутренними” координатами декомпозированной системы таких связей — ИМ, которые обеспечивают достижение аттрактора — поставленной цели управления.
  

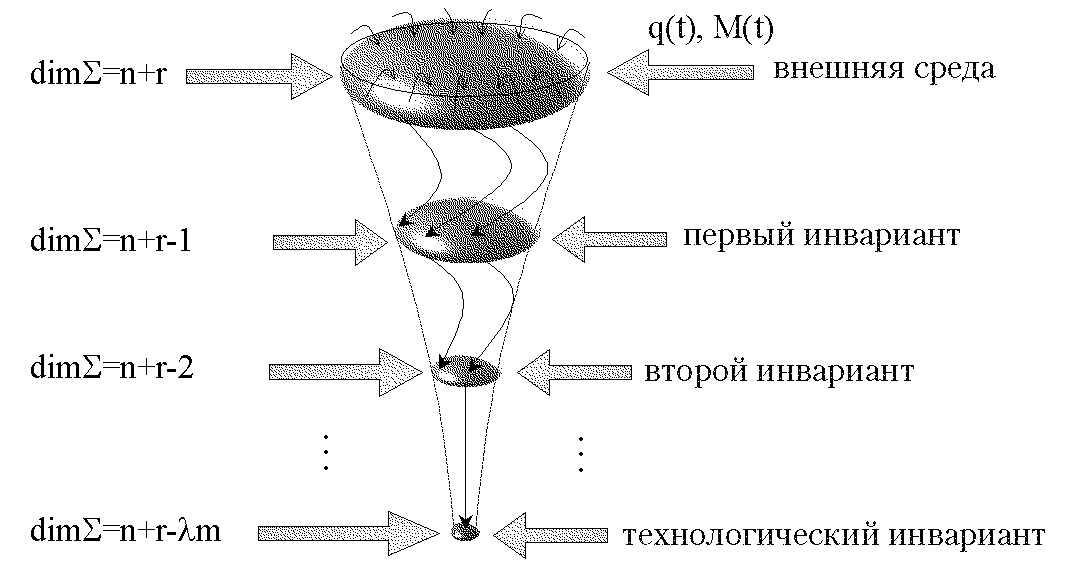
Рис. 2.7. Принцип “расширения — сжатия” пространства состояний систем

В результате возникает эффект асимптотической динамической декомпозиции и редукции синергетических систем на ИМ, который с особой силой проявляется в задачах векторного управления нелинейными многомерными объектами (рис. 2.7). В этом, наиболее сложном для теории управления, случае указанная декомпозиция в СТУ определяется соотношением
$$
\dim \Sigma = n+r - \lambda m,
$$где $n+r$ — размерность исходной расширенной системы, $m$ — размерность вектора управления, $\lambda$ — число вводимых ИМ. Отсюда следует, что с увеличением числа каналов управления процесс динамической декомпозиции систем значительно ускоряется, а процедура аналитического синтеза векторных законов управления, в отличие от известных методов теории управления, существенно упрощается. Это — эффект асимптотического упрощения синергетических систем. Итак, согласно СТУ, управление — это преодоление избыточных степеней свободы системы. Именно избыточность и инварианты приводят к организованному поведению замкнутой системы. Подчеркнем важное свойство этой постановки проблемы управления — сначала следует создать избыточные степени свободы, которые определяют дополнительные возможности в свойствах будущей системы, а затем преодолеть (редуцировать) эти степени свободы в процессе управления. В синергетике указанный процесс отражает свойство самоорганизации нелинейных систем. Процесс уменьшения числа степеней свободы возникает за счет сил взаимодействия наложенных связей в направлении от начального положения системы к промежуточным состояниям на некоторых ИМ последовательно понижающейся размерности ($\psi_1=0,\dots,\psi_m=0$) и далее к конечному целевому ИМ, т. е. происходит своего рода “эстафета аттракторов”. Свойства и направление этого процесса зависят не только от внешнего управления, а и от внутренней динамики нелинейного объекта. С точки зрения синергетики движение изображающей точки (ИТ) синтезируемых систем на финишных ИМ может быть интерпретировано как движение на желаемых диссипативных структурах, представляющих собой некоторые динамические состояния — аттракторы систем.

С математической точки зрения отличительная особенность постановки проблемы синергетического синтеза систем состоит в способе генерации такой совокупности обратных связей — законов управления $\mathbf u(\boldsymbol \psi) = \mathbf u(\mathbf x)$, которые переводят систему из произвольного исходного состояния сначала в окрестность желаемых многообразий $\psi_s(\mathbf x)=0$, а затем обеспечивают асимптотически устойчивое движение вдоль этих многообразий вплоть до попадания на целевой аттрактор. На этих аттракторах гарантируется выполнение заданных инвариантов — технологических, механических, энергетических и др. (рис. 2.6). При этом на траекториях движения системы достигается минимум сопровождающего оптимизирующего функционала
$$
\begin{equation*}
\mathbf J_\Sigma = \int \limits_0^\infty
\left[
\sum_{s=1}^m \phi_s^2(\psi_s) + \sum_{s=1}^m T_s^2 \dot{\psi_s^2}(t)
\right] dt \to \min,
\end{equation*}$$который отражает интегральные свойства систем и имеет ясный физический смысл. На его основе могут быть построены различные конкретные критерии оптимальности синтезируемых нелинейных систем управления [56, 58, 59].

С физической точки зрения на многообразиях $\psi_s=0$, вводимых в пространство состояний системы, происходит своего рода нерановесный фазовый переход. Такие многообразия формируют внутрисистемные динамические связи, в результате чего в фазовом пространстве системы возникает когерентное коллективное движение. Это позволяет реализовать направленную самоорганизацию коллективного состояния в нелинейных динамических системах. В развиваемом синергетическом подходе синтезируются законы управления, учитывающие внутренние кооперативные взаимодействия конкретных физических явлений и процессов. Этот подход позволит существенно продвинуться в решении поставленной академиком РАН А.А. Красовским [60] фундаментальной прикладной проблемы создания физической теории управления как проблемы поиска общих объективных законов управления. Введенный язык инвариантов, как основной элемент СТУ, позволяет придать этой теории естественно-математическое единство и установить непосредственную связь с законами сохранения, т. е. с основополагающими естественными свойствами объектов соответствующей природы.